Sample 26161: Predicted counts and count probabilities for poisson, negative binomial, ZIP, and ZINB models
 |  |  |  |  |
Predicted counts and count probabilities for Poisson, negative binomial, ZIP, and ZINB models
| Contents: | Purpose / History / Requirements / Usage / Details / Limitations / Missing Values / References |
Capabilities of this macro are now available from the SCORE statement in SAS/STAT® PROC PLM or the OUTPUT statement in SAS/ETS® PROC COUNTREG.
- PURPOSE:
- The PROBCOUNTS macro computes the predicted count and the predicted probabilities of specified counts for Poisson and negative binomial models and for zero-inflated versions of these models as fit by PROC COUNTREG in SAS/ETS software and PROC GENMOD or PROC NLMIXED in SAS/STAT software.
- HISTORY:
-
Version Update Notes 1.2 Added PROC= and INZEROMODEL= options to allow PROBCOUNTS to work with poisson, negative binomial, and (beginning in SAS 9.2) zero-inflated poisson models (not involving CLASS variables) fit by PROC GENMOD. 1.1 Added PRED= option. Removed need for MODEL= option. Renamed PARMS= to INMODEL=. Remove RESTRICT lines from COUNTREG parameters table. 1.0 Initial coding. - REQUIREMENTS:
- Only base SAS and SAS/STAT software are required to use the PROBCOUNTS macro. However, in order to create the required data set of parameter estimates, PROC COUNTREG in SAS/ETS software or PROC GENMOD in SAS/STAT software is required. PROC COUNTREG is available in SAS 9.1 TS1M3 Service Pack 3 or later. Draft documentation for the SAS 9.1 release of PROC COUNTREG (in PDF format) is available at this location. PROC COUNTREG in SAS 9.2 and later is documented in the SAS/ETS User's Guide (SAS Note 22930). PROC GENMOD can fit poisson and negative binomial models in SAS 8 or later, zero-inflated poisson (ZIP) models beginning in SAS 9.2, and zero-inflated negative binomial models beginning in SAS 9.2 TS2M3.
- USAGE:
- Before using the PROBCOUNTS macro, you must first run PROC COUNTREG, PROC GENMOD, or PROC NLMIXED to fit the desired model including an ODS OUTPUT statement to write the ParameterEstimates table (and, for a ZIP or ZINB model fit by PROC GENMOD, the ZeroParameterEstimates table) to a data set.
Follow the instructions in the Downloads tab of this sample to save the PROBCOUNTS macro definition. Replace the text within quotes in the following statement with the location of the PROBCOUNTS macro definition file on your system. In your SAS program or in the SAS editor window, specify this statement to define the PROBCOUNTS macro and make it available for use:
%inc "<location of your file containing the PROBCOUNTS macro>";
Following this statement, you may call the PROBCOUNTS macro. See the Results tab for an example.
The following are required:
- data=SAS-data-set
- Specifies that data set for which predicted values and/or predicted count probabilities are to be computed. The data set must contain all predictors specified in the MODEL and ZEROMODEL statements (including any offsets) when the model was fit.
- inmodel=ParameterEstimates-data-set
- Specifies the name of the data set created from the ParameterEstimates table. This must be the ParameterEstimates table saved using an ODS OUTPUT statement and not the OUTEST= data set.
- inzeromodel=ZeroParameterEstimates-data-set
- Specifies the name of the data set created from the ZeroParameterEstimates table of PROC GENMOD when it is used to fit a ZIP model. The ZEROMODEL statement used in PROC GENMOD must not involve CLASS variables. Use an ODS OUTPUT statement with PROC GENMOD to create this data set.
- proc=COUNTREG | GENMOD
- Specifies the procedure used to fit the model. If proc=GENMOD, the model cannot involve CLASS variables. For models fit using PROC NLMIXED, specify proc=COUNTREG. The default is COUNTREG.
One or both of the following must be specified:
- pred=name
- Names the variable to be added to the OUT= data set which will contain the predicted count for each observation in the DATA= data set. If omitted, the predicted count variable is not created in the OUT= data set.
- counts=number-list
- Specifies one or more nonnegative integers for which predicted probabilities are to be computed. For each integer, c, in the list, Pr(Y=c) is computed, where Y is the response variable. Number-list can be a single item or a list of items separated by commas. If commas appear in the list, then the entire list must be enclosed within %str( ). Each item can be an integer or a specification of the form x TO y BY z. If BY z is omitted, then BY 1 is assumed. For example,
counts=%str(0, 1, 2 to 10 by 2, 15)
requests predicted probabilities for values 0, 1, 2, 4, 6, 8, 10, and 15. If omitted, no predicted count probabilities are computed.
The following are optional:
- modeloffset=variable
- Specifies the offset variable if the OFFSET= option was specified in the MODEL statement when the model was fit.
- zerooffset=variable
- Specifies the offset variable if the OFFSET= option was specified in the ZEROMODEL statement when the model was fit in PROC COUNTREG. This option is not valid for models fit by PROC GENMOD since it does not offer an offset for the zero-inflation model.
- zerolink=LOGISTIC | NORMAL | PROBIT | CLOGLOG
- This option should match the LINK= option specified in the ZEROMODEL statement when the model was fit. Failure to do so will result in incorrect computations. Omit this option if the ZEROMODEL statement or the LINK= option was not specified. The default is LOGISTIC, as it is in the ZEROMODEL statements of PROC COUNTREG and PROC GENMOD.
- prefix=string
- Specifies a prefix to use in constructing names for the predicted count probability variables in the OUT= data set. If omitted, prefix=Pr resulting in variables names such as Pr0, Pr1, etc.
- out=SAS-data-set
- Specifies the name of the output data set. The PROBCOUNTS macro produces no displayed results. It only produces an output data set. This data set contains all variables and observations of the DATA= data set as well as the predicted count variable (if PRED= is specified) and/or the predicted count probability variables (if COUNTS= is specified). If omitted, the output data set is named PROBCOUNTS.
The version of the PROBCOUNTS macro that you are using is displayed when you specify version (or any string) as the first argument. For example:
%probcounts(version, data=mydata, inmodel=mymodel, pred=p)
- DETAILS:
- Poisson and negative binomial models can be fit by PROC COUNTREG in SAS/ETS software and by the GENMOD and GLIMMIX procedures in SAS/STAT software. PROC COUNTREG was first available as an experimental procedure in Service Pack 3 of SAS 9.1 (TS1M3). PROC COUNTREG can also estimate zero-inflated Poisson (ZIP) and negative binomial (ZINB) models. PROC GENMOD can also fit the ZIP model (beginning in SAS 9.2) and the ZINB model (beginning in SAS 9.2 TS2M3). All four models can be fit in PROC NLMIXED in SAS/STAT software by specifying the appropriate likelihood function. For Poisson and negative binomial models, PROC GENMOD and PROC GLIMMIX can provide predicted counts via their OUTPUT statements. In PROC NLMIXED, use the PREDICT statement. The PROBCOUNTS macro provides predicted counts for all four models as well as predicted count probabilities for counts that you specify.
For ZIP and ZINB models, two processes work together to produce the response: a Poisson or negative binomial process and a zero-inflation process. The first process generates zeros and positive integer values from a Poisson or negative binomial process. The second process is a binomial process which generates extra zeros. The probability of a zero in this second process, φ, is modeled via either a logit or probit model. The predictors, x, for the model of the first process, μ=exp(x'β), are specified in the MODEL statement of PROC COUNTREG or PROC GENMOD. The predictors, z, for the model of the second process, φ=F(z'γ) are specified in the ZEROMODEL statement of either procedure, and the model type (logit or probit) is specified in the LINK= option. The ZEROLINK= option in the PROBCOUNTS macro should match the LINK= option. If not, the computation of predicted counts and count probabilities will be incorrect. The ParameterEstimates table available from PROC COUNTREG or PROC NLMIXED contains the estimates of β and γ. In PROC GENMOD, the ParameterEstimates table contains the estimates of β and the ZeroParameterEstimates table contains the estimates of γ. In order to use the PROBCOUNTS macro with a model fit by PROC GENMOD, no CLASS variables can be specified in either the MODEL or ZEROMODEL statement.
The PROBCOUNTS macro requires as input the data set for which you want predicted counts and/or predicted count probabilities. This data set (specified in the DATA= option) may be the data set used to fit the model or another data set for which you want predicted values. In this way, the PROBCOUNTS macro can be used to score new observations using a previously fit model. The DATA= data set must contain all predictors specified in the MODEL and ZEROMODEL statements (including any offsets) when the model was fit. Also required as input is the data set of parameters from the fitted model, β and γ. For PROC COUNTREG or PROC NLMIXED, this data set (specified in the INMODEL= option) is created by including the following statement when fitting the model:
ods output ParameterEstimates = <SAS-data-set>;
For models fit by PROC GENMOD, the β parameters are input via the INMODEL= option and the γ parameters, in the case of ZIP models, are input via the INZEROMODEL= option. Both data sets can be created with this statement when fitting the model:
ods output ParameterEstimates = <SAS-data-set> ZeroParameterEstimates = <SAS-data-set>;Finally, you must specify either or both of the PRED= and COUNTS= options to request the desired predicted values.
The predicted count computed by the PROBCOUNTS macro for a given observation is an estimate of μ for Poisson and negative binomial models, or of μ(1-φ) for ZIP and ZINB models. For Poisson and negative binomial models, the predicted count probability for count c, p(c)=Pr(Y=c|x), is obtained directly from the Poisson or negative binomial probability mass function using the estimated mean for the given observation, μ. For ZIP or ZINB models, the predicted count probability is p(c)(1-φ)+I0φ, where I0=1 if c=0 and 0 otherwise.
The PROBCOUNTS macro produces no displayed results. It only produces an output data set.
The PROBCOUNTS macro attempts to check for a later version of itself. If it is unable to do this (such as if there is no active internet connection available), the macro will issue the following message:
PROBCOUNTS: Unable to check for newer version
The computation of predicted values is not affected by the appearance of this message.
- LIMITATIONS:
- Standard errors or confidence limits for the predicted counts are not currently available. The PROBCOUNTS macro cannot be used if a BY statement was specified in PROC COUNTREG. No predictor in the COUNTREG model should have a name beginning with "Restrict". In order to use the PROBCOUNTS macro with a model fit by PROC GENMOD, no CLASS variables can be specified in either the MODEL or ZEROMODEL statement. To use the PROBCOUNTS macro with models fit by PROC NLMIXED, you must rename the saved parameters such that the intercept is named Intercept, the dispersion parameter (if present) is named _Alpha, and the other parameters should have the name of the associated variable. Parameters in the inflation model should be named as just stated but with Inf_ as prefix.
- MISSING VALUES:
- If any predictor or offset variable in the model is missing, then the predicted count and predicted count probabilities are missing. If only the response variable is missing, predicted values are computed.
- REFERENCES:
- Long, J. S. (1990), "The origins of sex differences in science," Social Forces, 68, 1297-1315.
Long, J. S. (1997), Regression Models for Categorical and Limited Dependent Variables, Thousand Oaks: Sage Publications, Inc.
SAS Institute Inc. (2006), "The COUNTREG Procedure (Experimental)," Cary, NC: SAS Institute Inc.
These sample files and code examples are provided by SAS Institute Inc. "as is" without warranty of any kind, either express or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose. Recipients acknowledge and agree that SAS Institute shall not be liable for any damages whatsoever arising out of their use of this material. In addition, SAS Institute will provide no support for the materials contained herein.
These sample files and code examples are provided by SAS Institute Inc. "as is" without warranty of any kind, either express or implied, including but not limited to the implied warranties of merchantability and fitness for a particular purpose. Recipients acknowledge and agree that SAS Institute shall not be liable for any damages whatsoever arising out of their use of this material. In addition, SAS Institute will provide no support for the materials contained herein.
- EXAMPLE 1: ZIP and ZINB models for articles data using PROC COUNTREG
-
A study by Long (1990) examined the effects of gender (FEM), marital status (MAR),
number of young children (KID5), prestige of the graduate program (PHD), and the number of articles
published by scientists' mentors (MENT) on the number of articles published by
scientists (ART). PROC COUNTREG is used to fit Poisson and negative binomial
models to these data, as well as zero-inflated versions of these models (ZIP and ZINB models). For each model, the predicted probability of publishing m articles, m=0, 1, 2, ... , can be computed as the average predicted probability of m articles across all scientists. Of particular interest is the probability of zero articles published.
The following statements use PROC FREQ to compute the proportion of scientists publishing each observed number of articles.
proc freq data=articles; table art / out=obs; run;
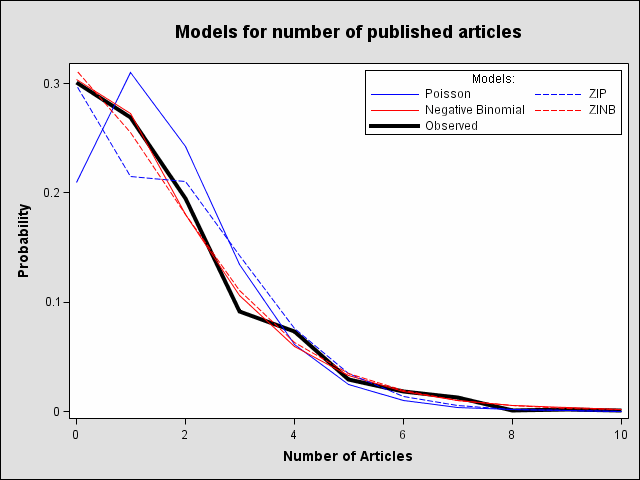
ART Frequency Percent Cumulative
FrequencyCumulative
Percent0 275 30.05 275 30.05 1 246 26.89 521 56.94 2 178 19.45 699 76.39 3 84 9.18 783 85.57 4 67 7.32 850 92.90 5 27 2.95 877 95.85 6 17 1.86 894 97.70 7 12 1.31 906 99.02 8 1 0.11 907 99.13 9 2 0.22 909 99.34 10 1 0.11 910 99.45 11 1 0.11 911 99.56 12 2 0.22 913 99.78 16 1 0.11 914 99.89 19 1 0.11 915 100.00 Note that the observed proportion publishing zero articles is 0.3005. If a single Poisson process generated these data, then the estimated Poisson mean is 1.69 (the average number of articles), and the probability of zero articles is Pr(art=0) = 1.690e-1.69/0! = e-1.69 = 0.18. This considerably underestimates the observed proportion. Under a single negative binomial process with the same estimated mean and with estimated dispersion parameter 0.5861 (which can be obtained by fitting an intercept-only model in PROC COUNTREG), the probability of zero articles is Pr(art=0) = 0.3085 which is much closer to the observed value. Given the parameters of the Poisson or negative binomial distribution, you can use the PDF function to obtain the probability of any number of articles.
The following statements use PROC COUNTREG to fit the Poisson model and the PROBCOUNTS macro to compute predicted count probabilities for counts 0 through 10 as variables POI0, POI1, ... , POI10 and saves them in data set PREDPOI. Under the Poisson model, the predicted proportion of zero articles is 0.2092 which, not surprisingly, is much closer to the probability from the single Poisson process (0.18) and considerably underestimates the observed proportion (0.30).
Note that syntax for the experimental SAS 9.1 version of PROC COUNTREG is shown below. The PROC COUNTREG syntax changed beginning in SAS 9.2. This example using production syntax is shown in the SAS/ETS User's Guide.
proc countreg data=articles type=poisson; model art = fem mar kid5 phd ment; ods output ParameterEstimates=pe; run; %probcounts(data=articles, inmodel=pe, counts=0 to 10, prefix=poi, out=predpoi)
The negative binomial model fit by the following statements more closely approximates the observed proportion of zeros (0.3036) as expected. Also, the test of the negative binomial dispersion parameter, _Alpha, in the negative binomial model indicates significant overdispersion in the Poisson model (p < .0001). As a result, the negative binomial model is preferred over the Poisson model. Predicted count probabilities are saved in data set PREDNB.
proc countreg data=articles type=negbin method=qn; model art = fem mar kid5 phd ment; ods output ParameterEstimates=pe; run; %probcounts(data=predpoi, inmodel=pe, counts=0 to 10, prefix=nb, out=prednb)
Another way to account for the large number of zeros in these data is to fit a zero-inflated Poisson (ZIP) or a zero-inflated negative binomial (ZINB) model. The following statements fit the ZIP model. In this ZIP model, all variables used to model the article counts are also used to model the extra zeros probability φ. The proportion of zeros predicted by the ZIP model is 0.2986 which is much closer to the observed proportion than was the Poisson model.
proc countreg data=articles type=zip; model art = fem mar kid5 phd ment / zi(var=fem mar kid5 phd ment); ods output ParameterEstimates=pe; run; %probcounts(data=prednb, inmodel=pe, counts=0 to 10, prefix=zip, out=predzip)
The following statements fit the ZINB model which also does a good job of estimating the proportion of zeros (0.3119) and it follows the other observed proportions well, though possibly not as well as the negative binomial model. The test for overdispersion again indicates a preference for the negative binomial version of the zero-inflated model (p < .0001).
proc countreg data=articles type=zinb method=qn; model art = fem mar kid5 phd ment / zi(var=fem mar kid5 phd ment); ods output ParameterEstimates=pe; run; %probcounts(data=predzip, inmodel=pe, counts=0 to 10, prefix=zinb, out=predzinb)
The following statements compute the average predicted count probability across all scientists for each count 0, 1, ... , 10. The averages for each model, along with the observed proportions, are then arranged for plotting.
/* For each model, compute the average probability at each count */ proc summary data=predzinb; var poi0-poi10 nb0-nb10 zip0-zip10 zinb0-zinb10; output out=mnpoi mean(poi0-poi10) =mn0-mn10; output out=mnnb mean(nb0-nb10) =mn0-mn10; output out=mnzip mean(zip0-zip10) =mn0-mn10; output out=mnzinb mean(zinb0-zinb10)=mn0-mn10; run; /* Arrange means for plotting and include the observed proportions */ data means; set mnpoi mnnb mnzip mnzinb; drop _type_ _freq_; run; proc transpose data=means out=tmeans; run; data allpred; merge obs(where=(art<=10)) tmeans; obs=percent/100; run;These statements use the ODS Graphics Template Language to produce the graph of the predicted probabilities for counts 0 through 10.
ods html; ods graphics on; proc template; define statgraph NumArt / store = SASUSER.TEMPLAT; notes "Several models for number of published articles"; layout lattice ; columnheader; entrytitle "Models for number of published articles" / padtop=10px padbottom=20px fontsize=16pt; endcolumnheader; layout overlay / xaxisopts=(label="Number of Articles") yaxisopts=(label="Probability"); series y=obs x=art / name="obs" legendlabel="Observed" linecolor=black linethickness=4px; series y=col1 x=art / name="poi" legendlabel="Poisson" linecolor=blue; series y=col2 x=art/ name="nb" legendlabel="Negative Binomial" linecolor=red; series y=col3 x=art/ name="zip" legendlabel="ZIP" linecolor=blue linepattern=dashshort; series y=col4 x=art/ name="zinb" legendlabel="ZINB" linecolor=red linepattern=dashshort; discretelegend "poi" "zip" "nb" "zinb" "obs" / title="Models:" halign=right valign=top across=2 down=3 border=on; endlayout; endlayout; end; run; title; data _null_; set allpred; file print ods=(template='NumArt'); put _ods_; run; ods graphics off; ods html close;For each of the four fitted models, the graph shows the average predicted count probability for each article count across all scientists. The poisson model clearly underestimates the proportion of zero articles published while the other three model are quite accurate at zero. All of the models fit the observed proportions well at the larger number of articles.
A similar plot can be created as follows with PROC GPLOT:
symbol1 v=none i=join c=black w=2; /* observed */ symbol2 v=none i=join c=green; /* obs'd univariate poisson */ symbol3 v=none i=join c=blue; /* poisson model */ symbol4 v=none i=join c=red; /* NB model */ symbol5 v=none i=join c=blue line=2; /* ZIP model */ symbol6 v=none i=join c=red line=2; /* ZINB model */ axis1 label=(angle=90 font=swissb "Probability") order=0 to 0.4 by .1 minor=none; axis2 label=(font=swissb "Number of Articles") order=0 to 10 minor=none; legend1 position=(middle center inside) mode=protect across=1 label=("Models:") offset=(,8 pct) frame value=("Observed" "Poisson" "ZIP" "NB" "ZINB"); proc gplot; plot obs*art=1 col1*art=3 col3*art=5 col2*art=4 col4*art=6 / overlay vaxis=axis1 haxis=axis2 legend=legend1; title "Models for number of published articles"; run; quit; - EXAMPLE 2: Predicted values for articles data
- In the above example, the negative binomial model appears to fit the observed data quite well. That model can now be used to generate predictions of the number of articles that would be produced by scientists at various settings of the predictors. Of interest is a comparison of married and unmarried male and female scientists to be made at a common setting of the number of mentor articles (MENT) and program prestige (PHD). The following statements find the means of these two predictors.
proc means data=articles; var ment phd; run;
Variable N Mean Std Dev Minimum Maximum MENT PHD 915 915 8.7672125 3.1031093 9.4839154 0.9842491 0 0.7550000 76.9999847 4.6199999 PROC FREQ reveals the distribution of young children for married and unmarried scientists.
proc freq data=articles; table mar*kid5; run;
Frequency
Percent
Row Pct
Col PctTable of MAR by KID5 MAR KID5 Total 0 1 2 3 0 309
33.77
100.00
51.590
0.00
0.00
0.000
0.00
0.00
0.000
0.00
0.00
0.00309
33.77
1 290
31.69
47.85
48.41195
21.31
32.18
100.00105
11.48
17.33
100.0016
1.75
2.64
100.00606
66.23
Total 599
65.46195
21.31105
11.4816
1.75915
100.00For married scientists, the mean number of young children is about 0.75.
proc means data=articles; where mar=1; var kid5; run;
Analysis Variable : KID5 N Mean Std Dev Minimum Maximum 606 0.7475248 0.8335638 0 3.0000000 The following creates the data set to be scored using the fitted negative binomial model. The predicted number of articles will be obtained for married and unmarried scientists of both genders at the averages of mentor articles, program prestige, and number of children given their marital status.
data toscore; input fem ment phd mar kid5; datalines; 0 8.76 3.10 0 0 0 8.76 3.10 1 .75 1 8.76 3.10 0 0 1 8.76 3.10 1 .75 ;The negative binomial model is again fit to the data and the estimated model parameters are stored in data set PE.
proc countreg data=articles type=negbin method=qn; model art = fem mar kid5 phd ment; ods output ParameterEstimates=pe; run;
The PROBCOUNTS macro is called using the PRED= option to create a variable, PREDCOUNT, containing the predicted counts for each observation in the TOSCORE data set. The results are saved in data set NBPREDS.
%probcounts(data=toscore, inmodel=pe, pred=predcount, out=NBpreds)The results show that male scientists produce a larger number of articles than female scientists, and that married scientists produce more articles than unmarried scientists.
proc print noobs; run;fem ment phd mar kid5 predcount 0 8.76 3.1 0 0.00 1.74760 0 8.76 3.1 1 0.75 1.77966 1 8.76 3.1 0 0.00 1.40752 1 8.76 3.1 1 0.75 1.43334
- EXAMPLE 3: Predicted values for articles data using PROC GENMOD
- The following statements fit the ZIP model from Example 1 above using PROC GENMOD in SAS 9.2 or later. The PROBCOUNTS macro is called to compute the predicted counts and predicted count probabilities for 0, 1, and 2 articles. The data set GENZIP is created containing the predicted count variable P and predicted count probability variables Pr0, Pr1, and Pr2.
proc genmod data=articles; model art = fem mar kid5 phd ment / dist=zip; zeromodel fem mar kid5 phd ment; ods output ParameterEstimates=pe ZeroParameterEstimates=zpe; run; %probcounts(data=articles, proc=genmod, inmodel=pe, inzeromodel=zpe, pred=p, counts=%str(0,1,2), out=GenZIP)
- EXAMPLE 4: Count probabilities for truncated model fit in PROC NLMIXED
- This note provides an example of fitting a truncated poisson model using PROC NLMIXED. After making the appropriate variable name changes in the ParameterEstimates table, the PROBCOUNTS macro is used to compute count probabilities.
Right-click on the link below and select Save to save
the PROBCOUNTS macro definition
to a file. It is recommended that you name the file
probcounts.sas.
Download and save probcounts.sas
| Type: | Sample |
| Topic: | SAS Reference ==> Procedures ==> COUNTREG SAS Reference ==> Procedures ==> GENMOD Analytics ==> Categorical Data Analysis Analytics ==> Regression SAS Reference ==> Procedures ==> NLMIXED |
| Date Modified: | 2008-11-17 15:01:39 |
| Date Created: | 2007-08-14 03:03:16 |
Operating System and Release Information
| Product Family | Product | Host | SAS Release | |
| Starting | Ending | |||
| SAS System | SAS/STAT | All | 9.1 TS1M3 | n/a |
| SAS System | SAS/ETS | All | 9.1 TS1M3 | n/a |