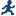Summary Statistics Task
About the Summary Statistics Task
The Summary Statistics
task provides descriptive statistics for variables across all observations
and within groups of observations. You can also summarize your data
in a graphical display, such as histograms and box plots.
For example, you could
use this task to create a report on the number of new sales, arranged
by product type and country.
Example: Summary Statistics of Unit Sales
Assigning Data to Roles
To run the Summary
Statistics task, you must assign a column to the Analysis
variables role.
|
Role
|
Description
|
|---|---|
|
Roles
|
|
|
Analysis
variables
|
The variables that you
assign to this role are the numeric variables for which you want statistics.
You must assign at least one variable to this role.
|
|
Classification
variables
|
The variables that you
assign to this role are character or discrete numeric variables that
are used to divide the input data into categories or subgroups. The
statistics are calculated on all selected analysis variables for each
unique combination of classification variables.
|
|
Additional Roles
|
|
|
Group analysis
by
|
The variables that you
assign to this role are used to compute separate statistics for each
distinct value or combination of values of the Group analysis by variables.
The data is automatically sorted by the variables in this role before
the statistics are computed.
|
|
Frequency
count
|
When you assign a variable
to this role, each observation in the table is assumed to represent n observations,
where n is the value of the
frequency count for that row. Statistics are calculated accordingly.
You can assign a maximum of one variable to this role.
|
|
Weight variable
|
If you assign a variable
to this role, the value of the variable for each observation is used
to calculate weighted means, variances, and sums. You can assign a
maximum of one variable to this role.
|
Setting Options
|
Option Name
|
Description
|
|---|---|
|
Statistics
|
|
|
Basic Statistics
|
|
|
Mean
|
is the arithmetic average,
calculated by adding the values of an analysis variable and dividing
this sum by the number of nonmissing observations.
|
|
Standard
deviation
|
is a statistical measure
of the variability of a group of data values. This measure, which
is the most widely used measure of the dispersion of a frequency distribution,
is equal to the positive square root of the variance.
|
|
Minimum
value
|
is the smallest value
for an analysis variable.
|
|
Maximum
value
|
is the largest value
for an analysis variable.
|
|
Median
|
is the middle value
for an analysis variable.
|
|
Number of
observations
|
is the total number
of observations with nonmissing values.
|
|
Number of
missing values
|
is the total number
of observations with missing values.
|
|
Additional Statistics
|
|
|
Standard
error
|
is the standard deviation
of the sample mean. The standard error is defined as the ratio of
the sample standard deviation to the square root of the sample size.
Note: This option is available
only if Degrees of freedom is selected in
the Divisor for standard deviation and variance drop-down
list.
|
|
Variance
|
is a statistical measure
of dispersion of data values. This measure is an average of the total
squared dispersion between each observation and the sample mean.
|
|
Mode
|
is the most frequent
value for the analysis variable.
|
|
Range
|
is the difference between
the largest and smallest values in the data.
|
|
Sum
|
is the sum of all values
in the analysis variable.
|
|
Sum of weights
|
is the sum of the numeric
variable that is used to weight each observation.
Note: You cannot compute the sum
of the weights unless you assign a variable to the Weight
variable role.
|
|
Confidence
limits for the mean
|
is the two-sided confidence
limits for the mean. A two-sided
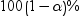 confidence interval for the mean has the following
upper and lower limits: confidence interval for the mean has the following
upper and lower limits: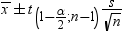 , where s is , where s is 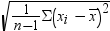 and and 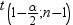 is the is the 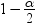 of the Student’s t statistics
with of the Student’s t statistics
with 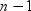 degrees of freedom. degrees of freedom.
|
|
Coefficient
of variation
|
is a unitless measure
of relative variability. This measure is defined as the ratio of the
standard deviation to the mean expressed as a percentage. The coefficient
of variation is meaningful only if the variable is measured on a ratio
scale.
|
|
Skewness
|
is skewness, which measures
the tendency of the deviations to be larger in one direction than
in the other.
|
|
Kurtosis
|
is the kurtosis, which
measures the heaviness of tails.
|
|
Percentiles
|
|
|
1st, 5th,
10th, Lower quartile, Median, Upper quartile, 90th, 95th, 99th, Interquartile
range
|
choose the percentiles
and quantiles to compute.
|
|
Quantile
method
|
specifies the method
that is used to compute the quantiles, median, and percentiles.
Order statistics
reads all of the data
into memory and sorts it by the unique values.
Piecewise-parabolic algorithm
approximates the quantile
and is a less memory-intensive method.
Note: If you assigned a variable
to the Weight variable role, only the Order
statistics method is available.
|
|
Plots
|
|
|
Histogram
|
creates a graph that
is used to determine the distribution of the data. If you add a normal
density curve, the task uses the sample mean and sample standard deviation
for
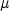 and and  . If you add a kernel density curve, the task uses
the AMISE method to compute the kernel density estimates. . If you add a kernel density curve, the task uses
the AMISE method to compute the kernel density estimates.
To include the statistics
in the graph, select the Add inset statistics check
box.
|
|
Comparative
box plot
|
creates a graph that
shows a measure of central location (the median), two measures of
dispersion (the range and interquartile range), the skewness (from
the orientation of the median relative to the quartiles), and potential
outliers. Box plots are especially useful in comparing two or more
sets of data.
Note: The Comparative
box plot option is available only when no column is assigned
to the Classification variable role.
You can choose to add
the overall inset statistics to the graph or only the inset statistics
for each group.
|
|
Histogram
and box plot
|
displays the histogram
and box plots together in a single panel, sharing common X axes. You
can choose to add the overall inset statistics to the graph.
Note: The Histogram
and box plot option is available only when no column
is assigned to the Classification variable role.
|
|
Details
|
|
|
Divisor
for standard deviation and variance
|
specifies the divisor
to use in the calculation of the variance and standard deviation.
Here are the valid options:
Degrees of freedom
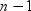 By default, the divisor
for the variance is the degrees of freedom.
Number of observations
n
Sum of weights minus one
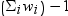 Sum of weights
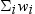 Note: The Sum of weights
minus one and the Sum of weights options
are available only if you assigned a variable to the Weight
variable role.
|
Copyright © SAS Institute Inc. All rights reserved.