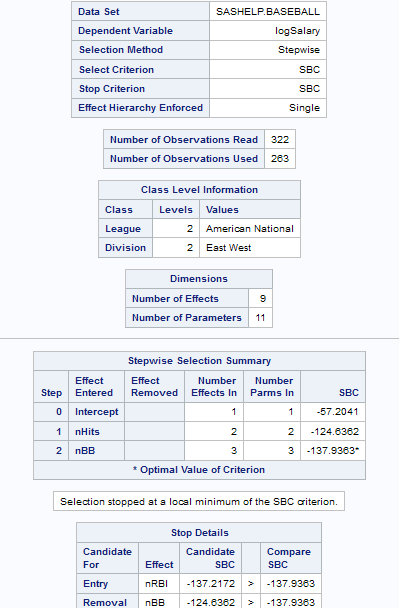
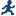Predictive Regression Model
About the Predictive Regression Model
The task is predictive
in that it selects the most influential effects based on observed
data. This task enables you to logically partition your data into
disjoint subsets for model training, validation, and testing. The
Predictive Regression Model task focuses on the standard independently
and identically distributed general linear model for univariate responses
and offers great flexibility and insight into the model selection
algorithm. This task can also create a scored data set. The results
for this task make it easy to explore the selected model in more detail
with other tasks, such as the Linear Regression task.
Partitioning Your Data
When you have sufficient
data, you can partition your data into three parts: training data,
validation data, and test data. During the selection process, models
are fit on the training data, and the prediction error for the model
is determined using the validation data. This prediction error can
be used to decide when to terminate the selection process or which
effects to include as the selection process proceeds. Finally, after
a model is selected, the test data can be used to assess how the selected
model generalizes on data that played no role in selecting the model.
You can partition your
data in either of these ways:
-
You can specify a proportion of the validation or test data. The proportions are used to divide the input data by sampling.
-
If the input data set contains a variable whose values indicate whether an observation is a validation or test case, you can specify the variable to use when partitioning the data. When you specify the variable, you also select the appropriate values for validation or test cases. The input data set is divided into partitions by using these values.
Assigning Data to Roles
To run the Predictive
Regression Model task, you must assign a column to the Dependent
variable role and a column to the Classification
variables role or the Continuous variables role.
|
Role
|
Description
|
|---|---|
|
Roles
|
|
|
Dependent
variable
|
specifies the numeric
variable to use as the dependent variable for the regression analysis.
|
|
Classification
variables
|
specifies the variables
to use to group (classify) data in the analysis. A classification
variable is a variable that enters the statistical analysis or model
through its levels, not through its values. The process of associating
values of a variable with levels is termed levelization.
|
|
Parameterization of
Effects
|
|
|
Coding
|
specifies the parameterization
method for the classification variable. Design matrix columns are
created from the classification variables according to the selected
coding scheme.
You can select from
these coding schemes:
|
|
Treatment of Missing
Values
|
|
|
An observation is excluded
from the analysis if any variable in the model contains a missing
value. In addition, an observation is excluded if any classification
variable specified earlier in this table contains a missing value,
regardless if it is used in the model.
|
|
|
Continuous
variables
|
specifies the independent
covariates (regressors) for the regression model. If you do not specify
a continuous variable, the task fits a model that contains only an
intercept.
|
|
Additional Roles
|
|
|
Frequency
count
|
lists a numeric variable
whose value represents the frequency of the observation. If you assign
a variable to this role, the task assumes that each observation represents n observations,
where n is the value of the frequency variable.
If n is not an integer, SAS truncates it. If n is
less than 1 or is missing, the observation is excluded from the analysis.
The sum of the frequency variable represents the total number of observations.
|
|
Weight
|
specifies the numeric
column to use as a weight to perform a weighted analysis of the data.
|
|
Group analysis
by
|
specifies to create
a separate analysis for each group of observations.
|
Building a Model
Requirements for Building a Model
To specify an effect,
you must assign at least one column to the Classification
variables role or the Continuous variables role.
You can select combinations of variables to create crossed, factorial,
or polynomial effects.
To create a model, use
the model builder on the Model tab. After
you create a model, you can specify whether to include the intercept
in the model.
Create a Nested Effect
Nested effects are specified
by following a main effect or crossed effect with a classification
variable or list of classification variables enclosed in parentheses.
The main effect or crossed effect is nested within the effects listed
in parentheses. Here are examples of nested effects: B(A), C(B*A),
D*E(C*B*A). In this example, B(A) is read "A nested within B."
Create N-Way Factorial
For example, if you
select the Height, Weight, and Age variables and then specify the
value of N as 2, when you click N-way Factorial,
these model effects are created: Age, Height, Weight, Age*Height,
Age*Weight, and Height*Weight. If N is set to a value greater than
the number of variables in the model, N is effectively set to the
number of variables.
Selecting a Model
|
Option Name
|
Description
|
|---|---|
|
Model Selection
|
|
|
Selection
method
|
By default, the complete
model that you specified is used to fit the model. However, you can
also use one of these selection methods:
|
|
Selection
method (continued)
|
Forward selection
specifies forward selection.
This method starts with no effects in the model and adds effects.
Backward elimination
specifies backward
elimination. This method starts with all effects in the model and
deletes effects.
Stepwise regression
specifies stepwise
regression, which is similar to the forward selection method except
that effects already in the model do not necessarily stay there.
LASSO
specifies the LASSO
method, which adds and deletes parameters based on a version of ordinary
least squares where the sum of the absolute regression coefficients
is constrained. If the model contains classification variables, these
classification variables are split.
Adaptive LASSO
requests that adaptive
weights be applied to each of the coefficients in the LASSO method.
The ordinary least squares estimates of the parameters in the model
are used in forming the adaptive weights.
|
|
Selection
method (continued)
|
Elastic net
specifies the elastic
net method, which is an extension of LASSO. The elastic net method
estimates parameters based on a version of ordinary least squares
in which both the sum of the absolute regression coefficients and
the sum of the squared regression coefficients are constrained. If
the model contains classification variables, these classification
variables are split.
Least angle regression
specifies least angle
regression. This method starts with no effects in the model and adds
effects. The parameter estimates at any step are “shrunk”
when compared to the corresponding least squares estimates. If the
model contains classification variables, these classification variables
are split.
|
|
Criterion
to add or remove effects
|
specifies the criterion
to use to determine whether an effect should be added or removed from
the model.
|
|
Criterion
to stop adding or removing effects
|
specifies the criterion
to use to determine whether effects should stop being added or removed
from the model.
|
|
Select best
model by
|
specifies the criterion
to use to determine the best fitting model.
|
|
Selection Statistics
|
|
|
Model fit
statistics
|
specifies which model
fit statistics are displayed in the fit summary table and the fit
statistics tables. If you select Default fit statistics,
the default set of statistics that are displayed in these tables includes
all the criteria used in model selection.
Here are the additional
fit statistics that you can include in the results:
|
|
Selection Plots
|
|
|
Criterion
plots
|
displays plots for these
criteria: adjusted R-square, Akaike’s information criterion,
Akaike’s information criterion corrected for small-sample bias,
and the criterion used to select the best fitting model. You can choose
to display these plots in a panel or individually.
|
|
Coefficient
plots
|
displays these plots:
|
|
Details
|
|
|
Selection
process details
|
specifies how much information
about the selection process to include in the results. You can display
a summary, details for each step of the selection process, or all
of the information about the selection process.
|
|
Model Effects Hierarchy
|
|
|
Model effects
hierarchy
|
specifies how the model
hierarchy requirement is applied and that only a single effect or
multiple effects can enter or leave the model at one time. For example,
suppose you specify the main effects A and B and the interaction A*B
in the model. In the first step of the selection process, either A
or B can enter the model. In the second step, the other main effect
can enter the model. The interaction effect can enter the model only
when both main effects have already been entered. Also, before A or
B can be removed from the model, the A*B interaction must first be
removed.
Model hierarchy refers
to the requirement that, for any term to be in the model, all effects
contained in the term must be present in the model. For example, in
order for the interaction A*B to enter the model, the main effects
A and B must be in the model. Likewise, neither effect A nor B can
leave the model while the interaction A*B is in the model.
|
|
Model effects
subject to the hierarchy requirement
|
specifies whether to
apply the model hierarchy requirement to the classification and continuous
effects in the model or to only the classification effects.
|
Setting the Options for the Final Model
|
Option Name
|
Description
|
|---|---|
|
Statistics for the Selected
Model
|
|
|
You can choose to include
the default statistics in the results or choose to include additional
statistics, such as the standardized regression coefficients. A standardized
regression coefficient is computed by dividing a parameter estimate
by the ratio of the sample standard deviation of the dependent variable
to the sample standard deviation of the regressor.
|
|
|
Collinearity
|
|
|
Collinearity
analysis
|
requests a detailed
analysis of collinearity among the regressors. This includes eigenvalues,
condition indices, and decomposition of the variances of the estimates
with respect to each eigenvalue.
|
|
Tolerance
values for estimates
|
produces tolerance values
for the estimates. Tolerance for a variable is defined as
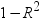 , where R square is obtained from the regression
of the variable on all other regressors in the model. , where R square is obtained from the regression
of the variable on all other regressors in the model.
|
|
Variance
inflation factors
|
produces variance inflation
factors with the parameter estimates. Variance inflation is the reciprocal
of tolerance.
|
|
Plots for the Selected
Model
|
|
|
Diagnostic and Residual
Plots
|
|
|
You must specify whether
to include the default diagnostic plots in the results. You can also
specify whether to include plots of the residuals for each explanatory
variable.
|
|
|
More Diagnostic Plots
|
|
|
Rstudent
statistic by predicted values
|
plots studentized residuals
by predicted values. If you select the Label extreme points option,
observations with studentized residuals that lie outside the band
between the reference lines
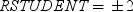 are deemed outliers. are deemed outliers.
|
|
DFFITS statistic
by observation number
|
plots the DFFITS statistic
by observation number. If you select the Label extreme
points option, observations with a DFFITS statistic greater
in magnitude than
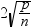 are deemed influential. The number of observations
used is n, and the number of regressors is p. are deemed influential. The number of observations
used is n, and the number of regressors is p.
|
|
DFBETAS
statistic by observation number for each explanatory variable
|
produces panels of DFBETAS
by observation number for the regressors in the model. You can view
these plots as a panel or as individual plots. If you select the Label
extreme points option, observations with a DFBETAS statistic
greater in magnitude than
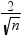 are deemed influential for that regressor. The number
of observations used is n. are deemed influential for that regressor. The number
of observations used is n.
|
|
Label extreme
points
|
identifies the extreme
values on each different type of plot.
|
|
Scatter Plots
|
|
|
Observed
values by predicted values
|
produces a scatter plot
of the observed values versus the predicted values.
|
|
Partial
regression plots for each explanatory variable
|
produces partial regression
plots for each regressor. If you display these plots in a panel, there
is a maximum of six regressors per panel.
|
|
Maximum
number of plot points
|
specifies the maximum
number of points to include in each plot.
|
Setting the Scoring Options
|
Option Name
|
Description
|
|---|---|
|
Scoring
|
|
|
You can create a scored
data set, which contains the predicted values and the residuals.
|
|
|
Add SAS
scoring code to the log
|
writes SAS DATA step
code for computing predicted values of the fitted model either to
a file or to a catalog entry. This code can then be included in a
DATA step to score new data.
|
Copyright © SAS Institute Inc. All rights reserved.