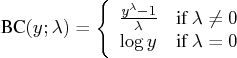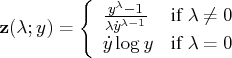Variable Transformations

Normalizing Transformations

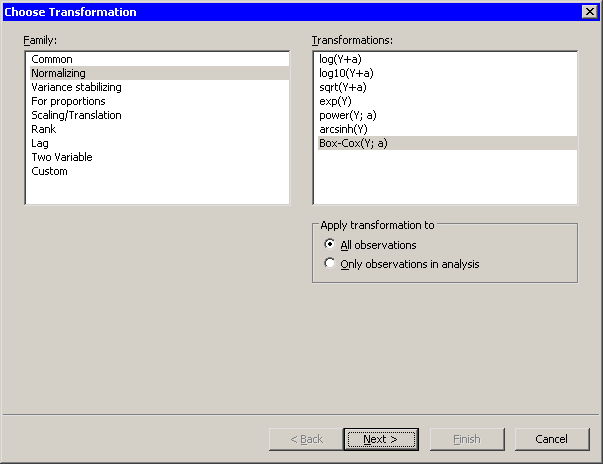
Figure 32.12 shows the transformations that are available when you select Normalizing from the Family list. These transformations are often used to improve the normality of a variable. Equations for these transformations are given in Table 32.2.

Figure 32.12: Normalizing Transformations

Table 32.2: Description of Normalizing Transformations

	Default	Name of
Transformation	Parameter	New Variable	Equation
log(Y+a)		Log_Y	$\log(y+a), y+a\gt$
log10(Y+a)		Log10_Y	$\log_{10}(y+a), y+a\gt$
sqrt(Y+a)		Sqrt_Y	$\sqrt{y+a}, y+a\gt$
exp(Y)		Exp_Y	$\exp(y)$
power(Y;a)		Pow_Y	$y^a, y\gt$ if is not integral
arcsinh(Y)		Arcsinh_Y	$\log(y+\sqrt{y^2+1})$
Box-Cox(Y;a)	MLE	BC_Y	See text.

The Box-Cox transformation (Box and Cox 1964) is a one-parameter family of power transformations that includes the logarithmic transformation as a limiting case. For $y\gt$ ,

${bc}(y;\lambda) = \{ \frac{y^\lambda - 1}{\lambda} & {if } \lambda \neq 0 \ \log y & {if } \lambda = 0 .$

You can specify the parameter, $\lambda$ , for the Box-Cox transformation, but typically you choose a value for $\lambda$ that maximizes (or nearly maximizes) a log-likelihood function.

Stat Studio plots the log-likelihood function versus the parameter, as shown in Figure 32.8. An inset gives the lower and upper 95% confidence limits for the maximum log-likelihood estimate, the MLE estimate, and a convenient estimate. A convenient estimate is a fraction with a small denominator (such as an integer, a half integer, or an integer multiple of or ) that is within the 95% confidence limits about the MLE. Although the value of the parameter is not bounded, Stat Studio graphs the log-likelihood function restricted to the interval .