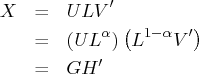| Multivariate Analysis: Principal Component Analysis |
Biplots
A biplot is a display that attempts to represent both the observations and variables of multivariate data in the same plot. Stat Studio provides biplots as part of the Principal Component analysis.
The computation of biplots in Stat Studio follows the presentation given in Friendly (1991) and Jackson (1991). Detailed discussions of how to compute and interpret biplots are available in Gabriel (1971) and Gower and Hand (1996).
The computation of a biplot begins with the data matrix. If you choose to compute principal components from the covariance matrix (on the Method tab; see Figure 26.3), then the data matrix is centered by subtracting the mean of each column. Otherwise, it is standardized so that each variable has zero mean and unit standard deviation.
In either case, let ![]() denote the resulting
denote the resulting ![]() matrix. The singular value decomposition (SVD) of
matrix. The singular value decomposition (SVD) of ![]() is the
factorization
is the
factorization
In a biplot, the rows of the ![]() matrix
matrix ![]() are plotted as
points, which correspond to observations. The rows of the
are plotted as
points, which correspond to observations. The rows of the ![]() matrix
matrix ![]() are plotted
as vectors, which correspond to variables.
are plotted
as vectors, which correspond to variables.
The choice of ![]() determines the scaling of the observations and
vectors in the biplot.
In general, it is impossible to accurately represent the variables and
observations in only two dimensions, but you can choose values of
determines the scaling of the observations and
vectors in the biplot.
In general, it is impossible to accurately represent the variables and
observations in only two dimensions, but you can choose values of
![]() that preserve certain properties of the high-dimensional
data. Common choices are
that preserve certain properties of the high-dimensional
data. Common choices are ![]() , and 1.
Stat Studio implements four different versions of the biplot:
, and 1.
Stat Studio implements four different versions of the biplot:
- GH

- This factorization uses
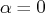 .
This biplot attempts to preserve relationships between variables.
This biplot has two useful properties:
.
This biplot attempts to preserve relationships between variables.
This biplot has two useful properties:
- The length of a vector (a row of
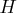 )
is proportional to the variance of the corresponding variable.
)
is proportional to the variance of the corresponding variable.
- The Euclidean distance between the
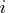 th and
th and 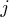 th rows of
th rows of 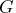 is proportional to the Mahalanobis distance between the
is proportional to the Mahalanobis distance between the 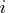 th and
th and 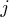 th
observations in the data set.
th
observations in the data set.
- The length of a vector (a row of
- JK

- This factorization uses
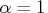 .
This biplot attempts to preserve the distance between observations.
This biplot has two useful properties:
.
This biplot attempts to preserve the distance between observations.
This biplot has two useful properties:
- The positions of the points in the biplot are identical to the score plot of first two principal components.
- The Euclidean distance between the
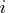 th and
th and 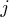 th rows of G
is equal to the Euclidean distance between the
th rows of G
is equal to the Euclidean distance between the 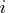 th and
th and 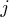 th
observations in the data set.
th
observations in the data set.
- SYM
- This factorization uses
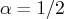 .
This biplot treats
observations and variables symmetrically.
This biplot attempts to preserve the values of observations.
.
This biplot treats
observations and variables symmetrically.
This biplot attempts to preserve the values of observations.
- COV
- This factorization uses
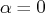 , but also multiplies
, but also multiplies 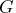 by
by
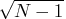 and divides
and divides  by the same quantity.
This biplot has two useful properties:
by the same quantity.
This biplot has two useful properties:
The axes at the bottom and left of the biplot are the coordinate axes for the observations. The axes at the top and right of the biplot are the coordinate axes for the vectors.
If the data matrix ![]() is not well approximated by a rank-two matrix, then
the visual information in the biplot is not a good approximation to
the data. In this case, you should not try to interpret the
biplot. However, if
is not well approximated by a rank-two matrix, then
the visual information in the biplot is not a good approximation to
the data. In this case, you should not try to interpret the
biplot. However, if ![]() is close to a rank-two matrix,
then you can interpret a biplot in the following ways:
is close to a rank-two matrix,
then you can interpret a biplot in the following ways:
- The cosine of the angle between a vector and an axis indicates the importance of the contribution of the corresponding variable to the axis dimension.
- The cosine of the angle between vectors indicates correlation between variables. Highly correlated variables point in the same direction; uncorrelated variables are at right angles to each other.
- Points that are close to each other in the biplot represent observations with similar values.
- You can approximate the coordinates of an observation by projecting the point onto the variable vectors within the biplot.
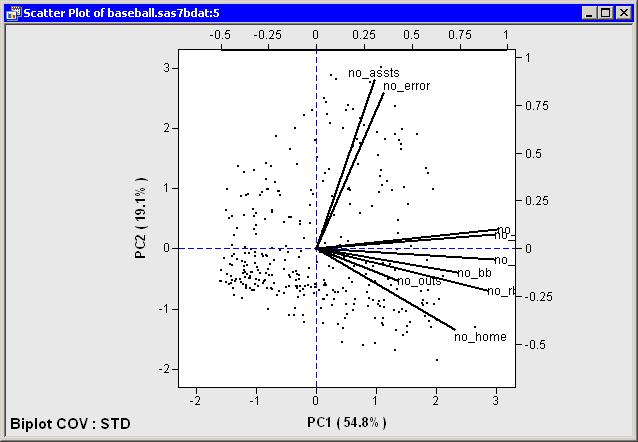
For example, in Figure 26.11 the two principal components account for approximately 74% of the variance in the data. This means that the biplot is a fair (but not good) approximation to the data. The footnote in the plot indicates that the biplot is based on the COV factorization and that the data matrix was standardized (STD).
The variables are grouped: the hitting variables point primarily in the direction of the horizontal axis; no_assts and no_error point primarily in the direction of the vertical axis. The no_outs vector is much shorter than the other vectors, which often indicates that the vector does not lie near the span of the two biplot dimensions.
The hitting variables are strongly correlated with each other. The variables no_assts and no_error are correlated with each other, but they are not correlated with the hitting variables or with no_outs.
Because the biplot is only a moderately good approximation to the data, the following statements are approximately true:
- The first and fourth quadrants contain players who tend to be strong hitters. The other quadrants contain weak hitters.
- The first and second quadrants contain players who tend to have many assists and errors. The other quadrants contain players with few assists and errors.
|
Figure 26.11: Biplot for Baseball Data
Copyright © 2008 by SAS Institute Inc., Cary, NC, USA. All rights reserved.