The STEPDISC Procedure

Displayed Output

The displayed output from PROC STEPDISC includes the class level information table. For each level of the classification variable, the following information is provided: the output data set variable name, frequency sum, weight sum, and the proportion of the total sample.

The optional output from PROC STEPDISC includes the following:

The optional output includes the following:

  • Within-class SSCP matrices for each group

  • Pooled within-class SSCP matrix

  • Between-class SSCP matrix

  • Total-sample SSCP matrix

  • Within-class covariance matrices for each group

  • Pooled within-class covariance matrix

  • Between-class covariance matrix, equal to the between-class SSCP matrix divided by $n(c-1)/c$, where n is the number of observations and c is the number of classes

  • Total-sample covariance matrix

  • Within-class correlation coefficients and 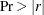$\mr{Pr} > |r|$ to test the hypothesis that the within-class population correlation coefficients are zero

  • Pooled within-class correlation coefficients and 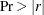$\mr{Pr} > |r|$ to test the hypothesis that the partial population correlation coefficients are zero

  • Between-class correlation coefficients and 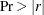$\mr{Pr} > |r|$ to test the hypothesis that the between-class population correlation coefficients are zero

  • Total-sample correlation coefficients and 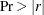$\mr{Pr} > |r|$ to test the hypothesis that the total population correlation coefficients are zero

  • Simple statistics, including N (the number of observations), sum, mean, variance, and standard deviation for the total sample and within each class

  • Total-sample standardized class means, obtained by subtracting the grand mean from each class mean and dividing by the total-sample standard deviation

  • Pooled within-class standardized class means, obtained by subtracting the grand mean from each class mean and dividing by the pooled within-class standard deviation

At each step, the following statistics are displayed:

  • for each variable considered for entry or removal: partial R-square, the squared (partial) correlation, the F statistic, and 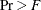$\mr{Pr} > F$, the probability level, from a one-way analysis of covariance

  • the minimum tolerance for entering each variable. A variable is entered only if its tolerance and the tolerances for all variables already in the model are greater than the value specified in the SINGULAR= option. The tolerance for the entering variable is 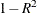$1 - R^2$ from regressing the entering variable on the other variables already in the model. 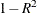The tolerance for a variable already in the model is $1 - R^2$ from regressing that variable on the entering variable and the other variables already in the model. With m variables already in the model, for each entering variable, m + 1 multiple regressions are performed by using the entering variable and each of the m variables already in the model as a dependent variable. These m + 1 tolerances are computed for each entering variable, and the minimum tolerance is displayed for each.

    The tolerance is computed by using the total-sample correlation matrix. It is customary to compute tolerance by using the pooled within-class correlation matrix (Jennrich 1977), but it is possible for a variable with excellent discriminatory power to have a high total-sample tolerance and a low pooled within-class tolerance. For example, PROC STEPDISC enters a variable that yields perfect discrimination (that is, produces a canonical correlation of one), but a program that uses pooled within-class tolerance does not.

  • the variable label, if any

  • the name of the variable chosen

  • the variables already selected or removed

  • Wilks’ lambda and the associated F approximation with degrees of freedom and 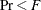$\mr{Pr} < F$, the associated probability level after the selected variable has been entered or removed. Wilks’ lambda is the likelihood ratio statistic for testing the hypothesis that the means of the classes on the selected variables are equal in the population (see the section Multivariate Tests in Chapter 4: Introduction to Regression Procedures.) Lambda is close to zero if any two groups are well separated.

  • Pillai’s trace and the associated F approximation with degrees of freedom and 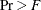$\mr{Pr} > F$, the associated probability level after the selected variable has been entered or removed. Pillai’s trace is a multivariate statistic for testing the hypothesis that the means of the classes on the selected variables are equal in the population (see the section Multivariate Tests in Chapter 4: Introduction to Regression Procedures).

  • Average squared canonical correlation (ASCC). The ASCC is Pillai’s trace divided by the number of groups minus 1. The ASCC is close to 1 if all groups are well separated and if all or most directions in the discriminant space show good separation for at least two groups.

  • Summary to give statistics associated with the variable chosen at each step. The summary includes the following:

    • Step number

    • Variable entered or removed

    • Number in, the number of variables in the model

    • Partial R-square

    • the F value for entering or removing the variable

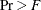    • $\mr{Pr} > F$, the probability level for the F statistic

    • Wilks’ lambda

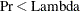    • $\mr{Pr} < \mr{Lambda}$ based on the F approximation to Wilks’ lambda

    • Average squared canonical correlation

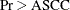    • $\mr{Pr} > \mr{ASCC}$ based on the F approximation to Pillai’s trace

    • the variable label, if any