The PRINCOMP Procedure
Example 91.3 Analyzing Job Ratings of Police Officers
This example uses the PRINCOMP procedure to analyze job performance. Police officers were rated by their supervisors in 14 categories as part of standard police department administrative procedure.
The following statements create the Jobratings data set:
options validvarname=any;
data Jobratings;
input 'Communication Skills'n 'Problem Solving'n
'Learning Ability'n 'Judgment Under Pressure'n
'Observational Skills'n 'Willingness to Confront Problems'n
'Interest in People'n 'Interpersonal Sensitivity'n
'Desire for Self-Improvement'n 'Appearance'n
'Dependability'n 'Physical Ability'n
'Integrity'n 'Overall Rating'n;
datalines;
2 6 8 3 8 8 5 3 8 7 9 8 6 7 7 4 7 5 8 8 7 6 8 5 7 6 6 7 5 6 7 5 7 8 6 3 7 7 5
8 7 5 6 7 8 6 9 7 7 7 9 8 8 9 9 7 9 9 9 9 7 7 9 8 8 7 8 8 8 8 8 9 8 9 7 8 9 9
8 8 8 7 9 9 8 9 9 9 9 8 8 9 8 9 9 7 9 8 8 7 7 9 4 7 9 8 4 6 8 8 8 6 3 5 6 5 2
... more lines ...
7 8 9 9 7 9 9 7 9 9 9 9 8 9 9 8 9 9 8 9 9 8 9 9 7 6 6 5 6 3 9 9 5 6 7 4 8 6
;
The Jobratings data set contains 14 variables. Each variable contains the job ratings, which use a scale measurement from 1 to 10 (1=fail
to comply, 10=exceptional). The last variable, Overall Rating, contains a score as an overall index of how each officer performs.
The following statements request a principal component analysis of the Jobratings data set, output the scores to the Scores data set (OUT= Scores), and produce default plots. Note that the variable Overall Rating is excluded from the analysis.
ods graphics on; proc princomp data=Jobratings(drop='Overall Rating'n); run;
Output 91.3.1 and Output 91.3.2 display the PROC PRINCOMP output, beginning with simple statistics and then the correlation matrix. By default, PROC PRINCOMP
computes principal components from the correlation matrix, so the total variance is equal to the number of variables, 13.
In this example, it would also be reasonable to use the COV option, which would cause variables that have a high variance
(such as Dependability) to influence the results more than variables that have a low variance (such as Learning Ability). If you used the COV option, scores would be computed from centered rather than standardized variables.
Output 91.3.1: Simple Statistics and Correlation Matrix from Using PROC PRINCOMP
| Simple Statistics | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Communication Skills | Problem Solving | Learning Ability | Judgment Under Pressure | Observational Skills | Willingness to Confront Problems |
Interest in People | Interpersonal Sensitivity | Desire for Self-Improvement | Appearance | Dependability | Physical Ability | Integrity | |
| Mean | 6.567567568 | 6.675675676 | 6.891891892 | 6.378378378 | 7.081081081 | 6.756756757 | 6.675675676 | 6.540540541 | 7.027027027 | 7.135135135 | 7.027027027 | 7.162162162 | 7.081081081 |
| StD | 1.878837414 | 1.748873511 | 1.696135866 | 2.252792728 | 1.816259563 | 2.126622327 | 1.871631108 | 2.218540494 | 1.707605316 | 1.436859271 | 1.499749729 | 1.343988953 | 1.460182226 |
| Correlation Matrix | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Communication Skills |
Problem Solving | Learning Ability | Judgment Under Pressure |
Observational Skills |
Willingness to Confront Problems |
Interest in People |
Interpersonal Sensitivity |
Desire for Self-Improvement |
Appearance | Dependability | Physical Ability | Integrity | |
| Communication Skills | 1.0000 | 0.7254 | 0.3685 | 0.6107 | 0.4338 | 0.5708 | 0.4646 | 0.2975 | 0.0211 | -.0086 | -.2619 | -.1145 | -.2096 |
| Problem Solving | 0.7254 | 1.0000 | 0.6715 | 0.6877 | 0.6207 | 0.6504 | 0.3828 | 0.3113 | 0.1890 | 0.1064 | -.0389 | -.0361 | -.1852 |
| Learning Ability | 0.3685 | 0.6715 | 1.0000 | 0.5126 | 0.7603 | 0.3545 | 0.1024 | 0.3112 | 0.3079 | 0.1885 | 0.0121 | 0.0932 | -.1085 |
| Judgment Under Pressure | 0.6107 | 0.6877 | 0.5126 | 1.0000 | 0.5761 | 0.6227 | 0.5635 | 0.4915 | 0.1489 | 0.1382 | -.1347 | -.1217 | -.1025 |
| Observational Skills | 0.4338 | 0.6207 | 0.7603 | 0.5761 | 1.0000 | 0.4655 | 0.2449 | 0.4921 | 0.4113 | 0.0915 | -.1640 | 0.0741 | -.0549 |
| Willingness to Confront Problems | 0.5708 | 0.6504 | 0.3545 | 0.6227 | 0.4655 | 1.0000 | 0.4751 | 0.2170 | 0.1931 | 0.1111 | 0.2286 | 0.1114 | -.1813 |
| Interest in People | 0.4646 | 0.3828 | 0.1024 | 0.5635 | 0.2449 | 0.4751 | 1.0000 | 0.5652 | 0.3765 | 0.2750 | 0.1220 | 0.0215 | 0.1115 |
| Interpersonal Sensitivity | 0.2975 | 0.3113 | 0.3112 | 0.4915 | 0.4921 | 0.2170 | 0.5652 | 1.0000 | 0.5460 | 0.4121 | 0.0790 | 0.1747 | 0.1747 |
| Desire for Self-Improvement | 0.0211 | 0.1890 | 0.3079 | 0.1489 | 0.4113 | 0.1931 | 0.3765 | 0.5460 | 1.0000 | 0.5645 | 0.2166 | 0.3248 | 0.3667 |
| Appearance | -.0086 | 0.1064 | 0.1885 | 0.1382 | 0.0915 | 0.1111 | 0.2750 | 0.4121 | 0.5645 | 1.0000 | 0.5525 | 0.3479 | 0.4183 |
| Dependability | -.2619 | -.0389 | 0.0121 | -.1347 | -.1640 | 0.2286 | 0.1220 | 0.0790 | 0.2166 | 0.5525 | 1.0000 | 0.5628 | 0.3415 |
| Physical Ability | -.1145 | -.0361 | 0.0932 | -.1217 | 0.0741 | 0.1114 | 0.0215 | 0.1747 | 0.3248 | 0.3479 | 0.5628 | 1.0000 | 0.5027 |
| Integrity | -.2096 | -.1852 | -.1085 | -.1025 | -.0549 | -.1813 | 0.1115 | 0.1747 | 0.3667 | 0.4183 | 0.3415 | 0.5027 | 1.0000 |
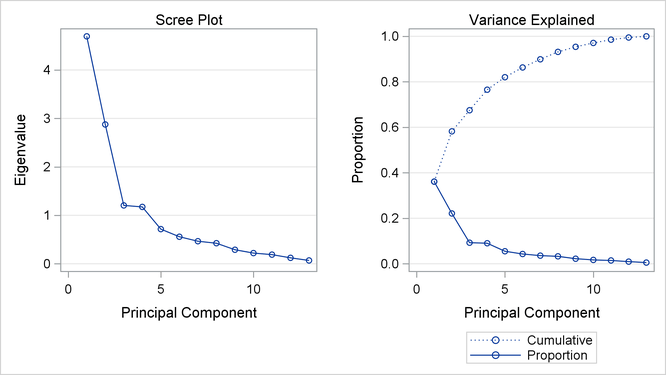
Output 91.3.2 displays the eigenvalues. The first principal component accounts for about 50% of the total variance, the second principal component accounts for about 13.6%, and the third principal component accounts for about 7.7%. Note that the eigenvalues sum to the total variance. The eigenvalues indicate that three to five components provide a good summary of the data: three components account for about 71.7% of the total variance, and five components account for about 82.7%. Subsequent components account for less than 5% each.
Output 91.3.2: Eigenvalues and Eigenvectors from Using PROC PRINCOMP
| Eigenvalues of the Correlation Matrix | ||||
|---|---|---|---|---|
| Eigenvalue | Difference | Proportion | Cumulative | |
| 1 | 4.69468687 | 1.81899683 | 0.3611 | 0.3611 |
| 2 | 2.87569003 | 1.67100277 | 0.2212 | 0.5823 |
| 3 | 1.20468727 | 0.03118935 | 0.0927 | 0.6750 |
| 4 | 1.17349791 | 0.45846322 | 0.0903 | 0.7653 |
| 5 | 0.71503470 | 0.15713583 | 0.0550 | 0.8203 |
| 6 | 0.55789887 | 0.09269082 | 0.0429 | 0.8632 |
| 7 | 0.46520805 | 0.04118763 | 0.0358 | 0.8990 |
| 8 | 0.42402041 | 0.13454552 | 0.0326 | 0.9316 |
| 9 | 0.28947489 | 0.06869311 | 0.0223 | 0.9539 |
| 10 | 0.22078178 | 0.03221769 | 0.0170 | 0.9708 |
| 11 | 0.18856410 | 0.06620108 | 0.0145 | 0.9853 |
| 12 | 0.12236302 | 0.05427092 | 0.0094 | 0.9948 |
| 13 | 0.06809210 | 0.0052 | 1.0000 | |
| Eigenvectors | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prin1 | Prin2 | Prin3 | Prin4 | Prin5 | Prin6 | Prin7 | Prin8 | Prin9 | Prin10 | Prin11 | Prin12 | Prin13 | |
| Communication Skills | 0.323548 | -.236730 | 0.206727 | 0.092655 | 0.293138 | 0.260352 | -.215988 | -.550645 | -.050648 | 0.107002 | 0.262509 | 0.341232 | 0.291574 |
| Problem Solving | 0.383857 | -.160898 | -.091224 | 0.212751 | 0.025258 | 0.252518 | -.140816 | -.104392 | 0.283104 | 0.221940 | -.548010 | -.492803 | -.073999 |
| Learning Ability | 0.322899 | -.050464 | -.553565 | 0.056656 | -.138393 | 0.168405 | 0.150062 | 0.055518 | 0.391053 | -.223399 | 0.132338 | 0.442471 | -.307096 |
| Judgment Under Pressure | 0.379958 | -.142821 | 0.155157 | -.025467 | 0.043612 | 0.175269 | 0.361045 | 0.391055 | -.315796 | -.392714 | -.286021 | 0.111225 | 0.382730 |
| Observational Skills | 0.359246 | -.067434 | -.424397 | -.148191 | 0.093417 | -.221005 | 0.022944 | 0.177808 | -.141401 | 0.225326 | 0.502509 | -.416669 | 0.278776 |
| Willingness to Confront Problems | 0.333754 | -.064285 | 0.183338 | 0.459764 | -.024447 | -.304704 | -.247094 | 0.259896 | -.387665 | 0.158552 | 0.047611 | 0.168464 | -.459746 |
| Interest in People | 0.296160 | 0.082187 | 0.575827 | -.140226 | 0.023973 | -.159653 | -.015476 | 0.131682 | 0.540942 | -.277206 | 0.299254 | -.197252 | -.112818 |
| Interpersonal Sensitivity | 0.302693 | 0.180810 | 0.119231 | -.432281 | -.047507 | -.238610 | 0.501550 | -.303435 | -.097727 | 0.393688 | -.196906 | 0.137833 | -.222427 |
| Desire for Self-Improvement | 0.225795 | 0.344251 | -.123236 | -.333516 | -.174557 | -.266896 | -.621875 | 0.020842 | 0.018350 | -.105222 | -.293349 | 0.219662 | 0.263644 |
| Appearance | 0.158341 | 0.425329 | 0.052469 | -.022665 | -.441729 | 0.494677 | -.051864 | -.204081 | -.350816 | -.186793 | 0.226289 | -.256802 | -.177399 |
| Dependability | 0.025597 | 0.427337 | 0.079019 | 0.520679 | -.289013 | -.044047 | 0.221520 | 0.079762 | 0.250326 | 0.336689 | 0.049300 | 0.146711 | 0.445532 |
| Physical Ability | 0.052980 | 0.418985 | -.185687 | 0.312555 | 0.486621 | -.299641 | 0.145579 | -.340453 | -.072184 | -.432711 | -.090520 | -.154868 | -.034075 |
| Integrity | -.006172 | 0.435225 | 0.015874 | -.147905 | 0.578186 | 0.421421 | -.087126 | 0.396179 | 0.030130 | 0.284351 | 0.021483 | 0.113790 | -.129601 |
PROC PRINCOMP produces the scree plot as shown in Output 91.3.3 by default when ODS Graphics is enabled. You can obtain more plots by specifying the PLOTS= option in the PROC PRINCOMP statement.
The scree plot on the left shows that the eigenvalue of the first component is approximately 6.5 and the eigenvalue of the second component is largely decreased to under 2.0. The variance explained plot on the right shows that the first four principal components account for nearly 80% of the total variance.
Output 91.3.3: Scree Plot from Using PROC PRINCOMP
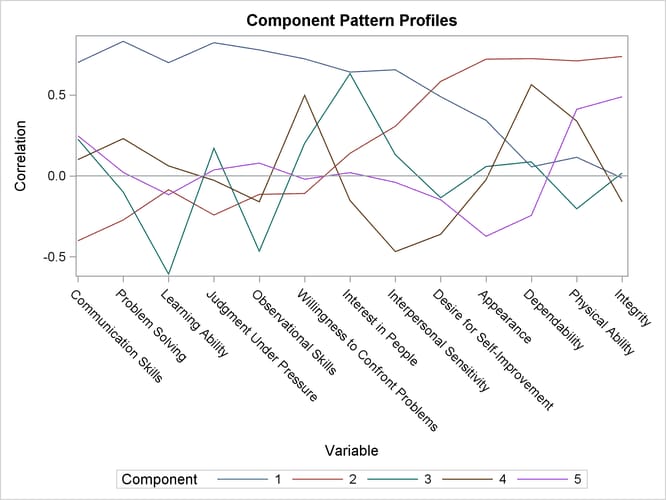
The first component reflects overall performance, because the first eigenvector shows approximately equal loadings on all
variables. The second eigenvector has high positive loadings on the variables Observational Skills and Willingness to Confront Problems but even higher negative loadings on the variables Interest in People and Interpersonal Sensitivity. This component seems to reflect the ability to take action, but it also reflects a lack of interpersonal skills. The third
eigenvector has a very high positive loading on the variable Physical Ability and high negative loadings on the variables Problem Solving and Learning Ability. This component seems to reflect physical strength, but it also shows poor learning and problem-solving skills.
In short, the three components represent the following:
- First component:
-
overall performance
- Second component:
-
smartness, toughness, and introversion
- Third component:
-
superior strength and average intellect
PROC PRINCOMP also produces other plots besides the scree plot, that help interpret the results. The following statements request plots from the PRINCOMP procedure:
proc princomp data=Jobratings(drop='Overall Rating'n)
n=5 plots(ncomp=3)=all;
run;
The N=5 option sets the number of principal components to five. The option PLOTS(NCOMP=3)=ALL produces all plots but limits to three the number of components that are displayed in the component pattern plots and the component score plots.
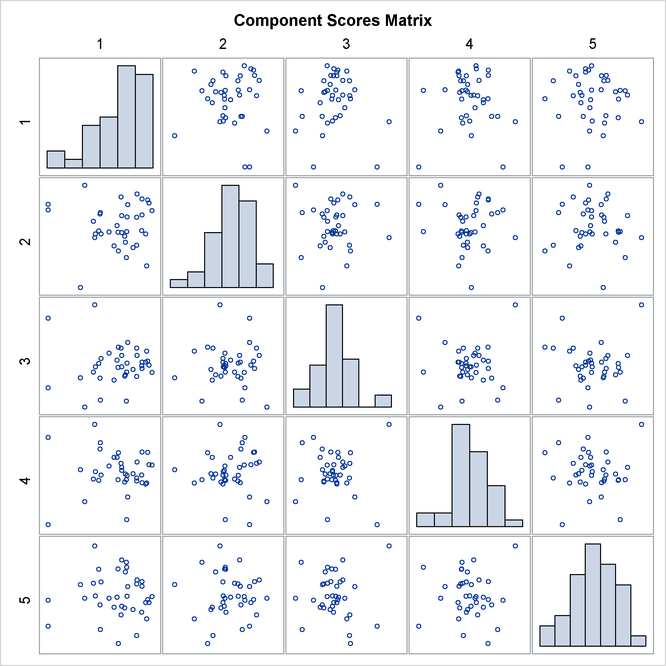
Output 91.3.4 shows a matrix plot of component scores for the first five principal components. The histogram of each component is displayed in the diagonal element of the matrix. The histograms indicate that the first principal component is skewed to the left and the second principal component is slightly skewed to the right.
Output 91.3.4: Matrix Plot of Component Scores
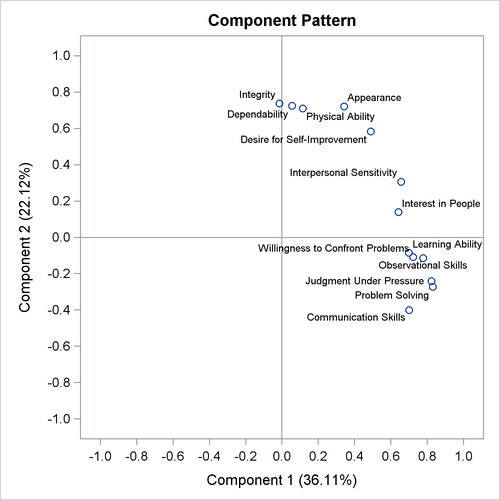
The pairwise component pattern plots are shown in Output 91.3.5 through Output 91.3.7. The pattern plots show the following:
-
All variables positively and evenly correlate with the first principal component (Output 91.3.5 and Output 91.3.6).
-
The variables
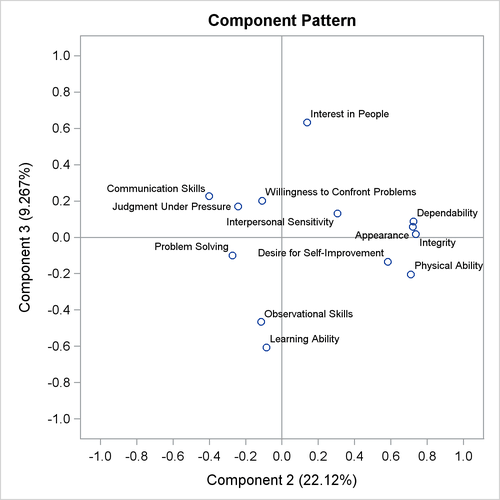
Observational SkillsandWillingness to Confront Problemscorrelate highly with the second component, and the variablesInterest in PeopleandInterpersonal Sensitivitycorrelate highly but negatively with the second component (Output 91.3.5). -
The variable
Physical Abilitycorrelates highly with the third component, and the variablesProblem SolvingandLearning Abilitycorrelate highly but negatively with the third component (Output 91.3.6). -
The variables
Observational Skills,Willingness to Confront Problems,Interest in People, andInterpersonal Sensitivitycorrelate highly (either positively or negatively) with the second component, but all these variables have very low correlations with the third component; the variablesPhysical AbilityandProblem Solvingcorrelate highly (either positively or negatively) with the third component, but both variables have very low correlations with the second component (Output 91.3.7).
Output 91.3.5: Pattern Plot of Component 2 by Component 1
Output 91.3.6: Pattern Plot of Component 3 by Component 1
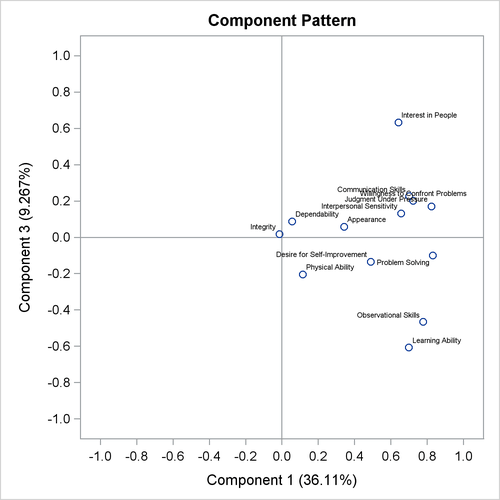
Output 91.3.7: Pattern Plot of Component 3 by Component 2
Output 91.3.8 shows a component pattern profile. As is shown in the pattern plots, the nearly horizontal profile from the first component indicates that the first component is mostly correlated evenly across all variables.
Output 91.3.8: Component Pattern Profile Plot from Using PROC PRINCOMP
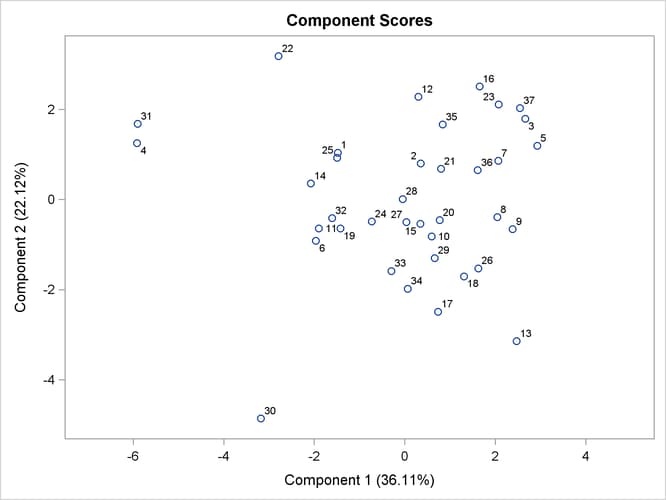
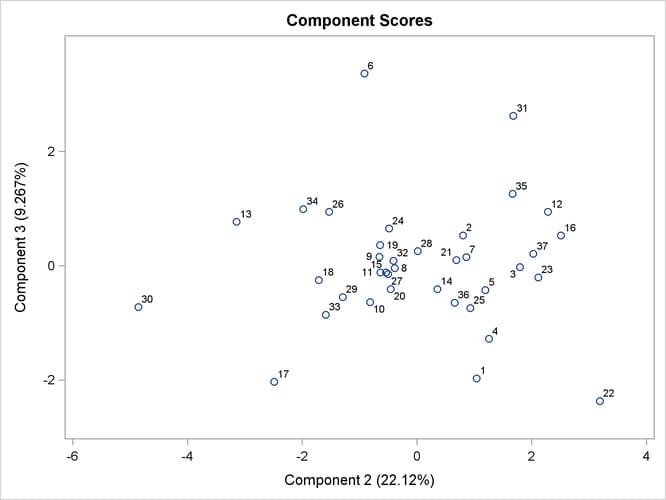
Output 91.3.9 through Output 91.3.11 display the pairwise component score plots. Observation numbers are used as the plotting symbol.
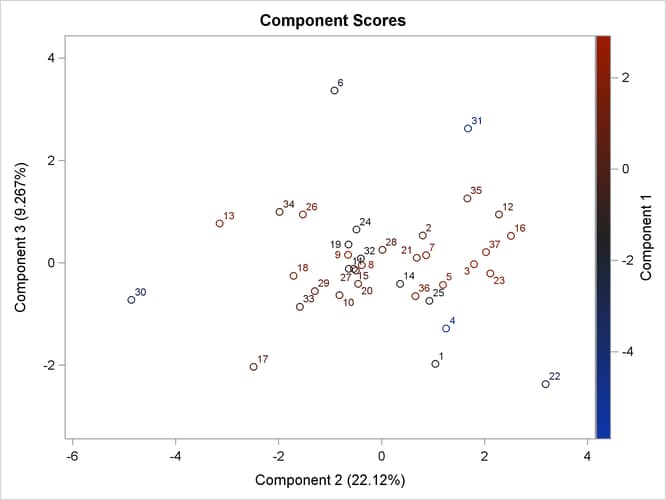
Output 91.3.9 shows a scatter plot of the first and second components. Observations 4 and 31 seem like outliers on the first component. Observations 22 and 30 can be potential outliers on the second component.
Output 91.3.9: Component 2 versus Component 1
Output 91.3.10 shows a scatter plot of the first and third components. Observations 4 and 31 seem like outliers on the first component.
Output 91.3.10: Component 3 versus Component 1
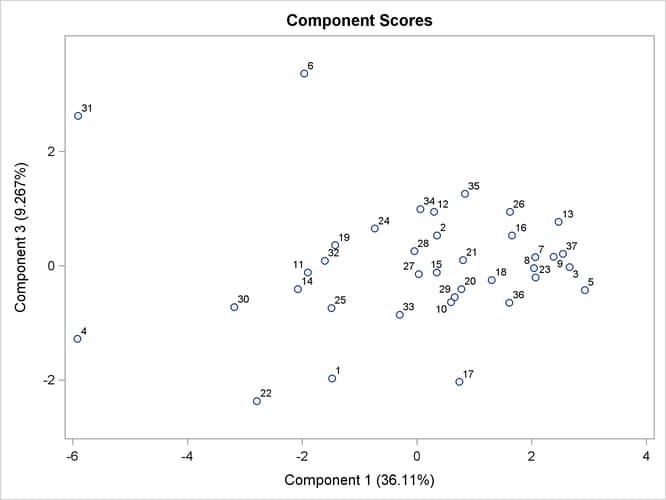
Output 91.3.11 shows a scatter plot of the second and third components. Observations 22 and 30 can be potential outliers on the second component.
Output 91.3.11: Component 3 versus Component 2
Output 91.3.12 shows a scatter plot of the second and third components, displaying the first component in color. Color interpolation ranges from red (minimum) to blue (middle) to green (maximum).
Output 91.3.12: Component 3 versus Component 2, Painted by Component 1