The PLM Procedure
Example 87.7 Linear Inference with Arbitrary Estimates
Suppose that you have calculated a vector of parameter estimates of dimension 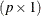 and its associated variance-covariance matrix by some statistical method. You might want to use these results to perform
linear inference, or to score a data set and calculate predicted values and their standard errors.
and its associated variance-covariance matrix by some statistical method. You might want to use these results to perform
linear inference, or to score a data set and calculate predicted values and their standard errors.
The following DATA steps create two SAS data sets. The first, called parms, contains six estimates that represent two uncorrelated groups. The data set cov contains the covariance matrix of the estimates. The lack of correlation between the two sets of three parameters is evident
in the block-diagonal structure of the covariance matrix.
data parms; length name $6; input Name$ Value; datalines; alpha1 -3.5671 beta1 0.4421 gamma1 -2.6230 alpha2 -3.0111 beta2 0.3977 gamma2 -2.4442 ;
data cov; input Parm row col1-col6; datalines; 1 1 0.007462 -0.005222 0.010234 0.000000 0.000000 0.000000 1 2 -0.005222 0.048197 -0.010590 0.000000 0.000000 0.000000 1 3 0.010234 -0.010590 0.215999 0.000000 0.000000 0.000000 1 4 0.000000 0.000000 0.000000 0.031261 -0.009096 0.015785 1 5 0.000000 0.000000 0.000000 -0.009096 0.039487 -0.019996 1 6 0.000000 0.000000 0.000000 0.015785 -0.019996 0.126172 ;
Suppose that you are interested in testing whether the parameters are homogeneous across groups—that is, whether 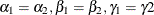 . You are interested in testing the hypothesis jointly and separately with multiplicity adjustment.
. You are interested in testing the hypothesis jointly and separately with multiplicity adjustment.
To use the PLM procedure, you first need to create an item store that contains the necessary information as if the preceding parameter vector and covariance matrix were the result of a statistical modeling procedure. The following statements use the GLIMMIX procedure to create such an item store, by fitting a saturated linear model with the data set that contains the parameter estimates serving as the input data set:
proc glimmix data=parms order=data; class Name; model Value = Name / noint ddfm=none s; random _residual_ / type=lin(1) ldata=cov v; parms (1) / noiter; store ArtificialModel; title 'Linear Inference'; run;
The RANDOM statement is used to form the covariance structure for the estimates. The PARMS statement prevents iterative updates
of the covariance parameters. The resulting marginal covariance matrix of the "data" is thus identical to the covariance matrix
in the data set cov. The ORDER=DATA option in the PROC GLIMMIX statement is used to arrange the levels of the classification variable Name in the order in which they appear in the data set so that the order of the parameters matches that of the covariance matrix.
The results of this analysis are shown in Output 87.7.1. Note that the parameter estimates are identical to the values passed in the input data set and their standard errors equal
the square root of the diagonal elements of the cov data set.
Output 87.7.1: "Fitted" Parameter Estimates and Covariance Matrix
| Solutions for Fixed Effects | ||||||
|---|---|---|---|---|---|---|
| Effect | name | Estimate | Standard Error |
DF | t Value | Pr > |t| |
| name | alpha1 | -3.5671 | 0.08638 | Infty | -41.29 | <.0001 |
| name | beta1 | 0.4421 | 0.2195 | Infty | 2.01 | 0.0440 |
| name | gamma1 | -2.6230 | 0.4648 | Infty | -5.64 | <.0001 |
| name | alpha2 | -3.0111 | 0.1768 | Infty | -17.03 | <.0001 |
| name | beta2 | 0.3977 | 0.1987 | Infty | 2.00 | 0.0454 |
| name | gamma2 | -2.4442 | 0.3552 | Infty | -6.88 | <.0001 |
There are other ways to fit a saturated model with the GLIMMIX procedure. For example, you can use the TYPE=UN covariance structure in the RANDOM statement with a properly prepared input data set for the PDATA= option in the PARMS statement. See Example 17 in Examples: GLIMMIX Procedure: Examples: GLIMMIX Procedure, for details.
Once the item store exists, you can apply the linear inference capabilities of the PLM procedure. For example, the ESTIMATE statement in the following statements test the hypothesis of parameter homogeneity across groups:
proc plm restore=ArtificialModel;
estimate
'alpha1 = alpha2' Name 1 0 0 -1 0 0,
'beta1 = beta2 ' Name 0 1 0 0 -1 0,
'gamma1 = gamma2' Name 0 0 1 0 0 -1 /
adjust=bon stepdown ftest(label='Homogeneity');
run;
Output 87.7.2: Results from the PLM Procedure
| Linear Inference |
| Estimates Adjustment for Multiplicity: Holm |
||||||
|---|---|---|---|---|---|---|
| Label | Estimate | Standard Error | DF | t Value | Pr > |t| | Adj P |
| alpha1 = alpha2 | -0.5560 | 0.1968 | Infty | -2.83 | 0.0047 | 0.0142 |
| beta1 = beta2 | 0.04440 | 0.2961 | Infty | 0.15 | 0.8808 | 1.0000 |
| gamma1 = gamma2 | -0.1788 | 0.5850 | Infty | -0.31 | 0.7599 | 1.0000 |
The F test in Output 87.7.2 shows that the joint test of homogeneity is rejected. The individual tests with familywise control of the Type I error show
that the overall difference is due to a significant change in the  parameters. The hypothesis of homogeneity across the two groups cannot be rejected for the
parameters. The hypothesis of homogeneity across the two groups cannot be rejected for the 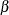 and
and 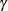 parameters.
parameters.
