The PLM Procedure

Analysis Based on Posterior Estimates

If an item store is saved from a Bayesian analysis (by PROC GENMOD or PROC PHREG or PROC LIFEREG), then PROC PLM can perform sampling-based inference based on Bayes posterior estimates that are saved in the item store. For example, the following statements request a Bayesian analysis and save the results to an item store named sasuser.gmd. For the Bayesian analysis, the random number generator seed is set to 1. By default, a noninformative distribution is set as the prior distribution for the regression coefficients and the posterior sample size is 10,000.

proc genmod data=gs;
   class a b;
   model y = a b;
   bayes seed=1;
   store sasuser.gmd / label='Bayesian Analysis';
run;

When the PLM procedure opens the item store sasuser.gmd, it detects that the results were saved from a Bayesian analysis. The posterior sample of regression coefficient estimates are then loaded to perform statistical inference tasks.

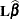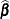The majority of postprocessing tasks involve inference based on an estimable linear function $\mb{L}\widehat{\bbeta }$ , which often requires its mean and variance. When the standard frequentist analyses are performed, the mean and variance have explicit forms because the parameter estimate $\widehat{\bbeta }$ is analytically tractable. However, explicit forms are not usually available when Bayesian models are fitted. Instead, empirical means and variance-covariance matrices for the estimable function are constructed from the posterior sample.

Let 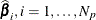$\widehat{\bbeta }_ i,i=1,\dots ,N_ p$ denote the 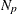$N_ p$ vectors of posterior sample estimates of 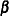$\bbeta$ saved in sasuser.gmd. Use these vectors to construct the posterior sample of estimable functions 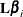$\mb{L}{\bbeta }_ i$ . The posterior mean of the estimable function is thus

$\overline{\mb{L}\widehat{\bbeta }}=\frac{1}{N_ p} \sum _{i=1}^{N_ p}\mb{L}\widehat{\bbeta }_ i$

and the posterior variance of the estimable function is

$\mb{V}\left(\mb{L}\widehat{\bbeta }\right)= \frac{1}{N_ p-1}\sum _{i=1}^{N_ p}\left(\mb{L}\widehat{\bbeta }_ i- \overline{\mb{L}\widehat{\bbeta }}\right)^2$

Sometimes statistical inference on a transformation of 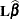$\mb{L}\widehat{\bbeta }$ is requested. For example, the EXP option for the ESTIMATE and LSMESTIMATE statements requests analysis based on 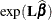$\exp (\mb{L}\widehat{\bbeta })$ , exponentiation of the estimable function. If this type of analysis is requested, the posterior sample of transformed estimable functions is constructed by transforming each of the estimable function evaluated at the posterior sample: 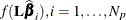$f(\mb{L}\widehat{\bbeta }_ i),i=1,\dots ,N_ p$ . The posterior mean and variance for 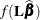$f(\mb{L}\widehat{\bbeta })$ are then computed from the constructed sample to make the inference:

$\overline{f(\mb{L}\widehat{\bbeta })}=\frac{1}{N_ p} \sum _{i=1}^{N_ p}f(\mb{L}\widehat{\bbeta }_ i)$

$\mb{V}\left(f(\mb{L}\widehat{\bbeta })\right)= \frac{1}{N_ p-1}\sum _{i=1}^{N_ p}\left(f(\mb{L}\widehat{\bbeta }_ i)- \overline{f(\mb{L}\widehat{\bbeta })}\right)^2$

After obtaining the posterior mean and variance, the PLM procedure proceeds to perform statistical inference based on them.