Introduction to Statistical Modeling with SAS/STAT Software
Linear Model Theory
Subsections:
This section presents some basic statistical concepts and results for the linear model with homoscedastic, uncorrelated errors in which the parameters are estimated by ordinary least squares. The model can be written as
![\[ \bY = \bX \bbeta + \bepsilon \quad \quad \bepsilon \sim (0,\sigma ^2\mb{I}) \]](images/statug_intromod0332.png)
where 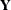 is an
is an 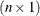 vector and
vector and 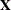 is an
is an 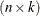 matrix of known constants. The model equation implies the following expected values:
matrix of known constants. The model equation implies the following expected values:
![\begin{align*} \mr{E}[\bY ] =& \, \, \bX \bbeta \\ \mr{Var}[\bY ] =& \, \, \sigma ^2\bI \Leftrightarrow \mr{Cov}[Y_ i,Y_ j] = \left\{ \begin{array}{ll} \sigma ^2 & i = j \cr 0 & \mbox{otherwise} \end{array} \right. \end{align*}](images/statug_intromod0333.png)