Introduction to Statistical Modeling with SAS/STAT Software
Estimating the Error Variance
The least squares principle does not provide for a parameter estimator for 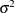 . The usual approach is to use a method-of-moments estimator that is based on the sum of squared residuals. If the model is
correct, then the mean square for error, defined to be
. The usual approach is to use a method-of-moments estimator that is based on the sum of squared residuals. If the model is
correct, then the mean square for error, defined to be 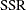 divided by its degrees of freedom,
divided by its degrees of freedom,
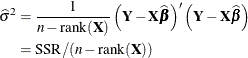
is an unbiased estimator of 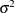 .
.