The GLMSELECT Procedure

Breiman, L. (1992). “The Little Bootstrap and Other Methods for Dimensionality Selection in Regression: X-Fixed Prediction Error.” Journal of the American Statistical Association 87:738–754.

Burnham, K. P., and Anderson, D. R. (2002). Model Selection and Multimodel Inference. 2nd ed. New York: Springer-Verlag.

Darlington, R. B. (1968). “Multiple Regression in Psychological Research and Practice.” Psychological Bulletin 69:161–182.

Donoho, D. L., and Johnstone, I. M. (1994). “Ideal Spatial Adaptation via Wavelet Shrinkage.” Biometrika 81:425–455.

Draper, N. R., Guttman, I., and Kanemasu, H. (1971). “The Distribution of Certain Regression Statistics.” Biometrika 58:295–298.

Efron, B., Hastie, T. J., Johnstone, I. M., and Tibshirani, R. (2004). “Least Angle Regression (with Discussion).” Annals of Statistics 32:407–499.

Efron, B., and Tibshirani, R. J. (1993). An Introduction to the Bootstrap. New York: Chapman & Hall.

Eilers, P. H. C., and Marx, B. D. (1996). “Flexible Smoothing with B-Splines and Penalties.” Statistical Science 11:89–121. With discussion.

El Ghaoui, L., Viallon, V., and Rabbani, T. (2012). “Safe Feature Elimination for the Lasso and Sparse Supervised Learning Problems.” Pacific Journal of Optimization 8:667–698. Special issue on conic optimization.

Fan, J., and Lv, J. (2008). “Sure Independence Screening for Ultrahigh Dimensional Feature Space.” Journal of the Royal Statistical Society, Series B 70:849–911.

Foster, D. P., and Stine, R. A. (2004). “Variable Selection in Data Mining: Building a Predictive Model for Bankruptcy.” Journal of the American Statistical Association 99:303–313.

Golub, T. R., Slonim, D. K., Tamayo, P., Huard, C., Gaasenbeek, M., Mesirov, J. P., Coller, H., Loh, M., Downing, J. R., Caligiuri, M. A., Bloomfield, C. D., and Lander, E. S. (1999). “Molecular Classification of Cancer: Class Discovery and Class Prediction by Gene Expression.” Science 286:531–537.

Harrell, F. E. (2001). Regression Modeling Strategies. New York: Springer-Verlag.

Hastie, T. J., Tibshirani, R. J., and Friedman, J. H. (2001). The Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York: Springer-Verlag.

Hocking, R. R. (1976). “The Analysis and Selection of Variables in a Linear Regression.” Biometrics 32:1–50.

Hurvich, C. M., Simonoff, J. S., and Tsai, C.-L. (1998). “Smoothing Parameter Selection in Nonparametric Regression Using an Improved Akaike Information Criterion.” Journal of the Royal Statistical Society, Series B 60:271–293.

Hurvich, C. M., and Tsai, C.-L. (1989). “Regression and Time Series Model Selection in Small Samples.” Biometrika 76:297–307.

Judge, G. G., Griffiths, W. E., Hill, R. C., Lütkepohl, H., and Lee, T.-C. (1985). The Theory and Practice of Econometrics. 2nd ed. New York: John Wiley & Sons.

Liu, J., Zhao, Z., Wang, J., and Ye, J. (2014). “Safe Screening with Variational Inequalities and Its Application to Lasso.” In JMLR Workshop and Conference Proceedings, Vol. 32: Proceedings of the Thirty-First International Conference on Machine Learning, Second Cycle. http://jmlr.org/proceedings/papers/v32/liuc14.pdf.

Mallows, C. L. (1967). “Choosing a Subset Regression.” Bell Telephone Laboratories.

Mallows, C. L. (1973). “Some Comments on 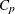.” Technometrics 15:661–675.

Miller, A. J. (2002). Subset Selection in Regression. Vol. 95 of Monographs on Statistics and Applied Probability. 2nd ed. Boca Raton, FL: Chapman & Hall/CRC.

Nesterov, Y. (2013). “Gradient Methods for Minimizing Composite Objective Function.” Mathematical Programming 140:125–161.

Osborne, M. R., Presnell, B., and Turlach, B. A. (2000). “A New Approach to Variable Selection in Least Squares Problems.” IMA Journal of Numerical Analysis 20:389–404.

Raftery, A. E., Madigan, D., and Hoeting, J. A. (1997). “Bayesian Model Averaging for Linear Regression Models.” Journal of the American Statistical Association 92:179–191.

Reichler, J. L., ed. (1987). The 1987 Baseball Encyclopedia Update. New York: Macmillan.

Sarle, W. S. (2001). “Donoho-Johnstone Benchmarks: Neural Net Results.” Accessed March 27, 2007. ftp://ftp.sas.com/pub/neural/dojo/dojo.html.

Sawa, T. (1978). “Information Criteria for Discriminating among Alternative Regression Models.” Econometrica 46:1273–1282.

Schwarz, G. (1978). “Estimating the Dimension of a Model.” Annals of Statistics 6:461–464.

Tibshirani, R. (1996). “Regression Shrinkage and Selection via the Lasso.” Journal of the Royal Statistical Society, Series B 58:267–288.

Tibshirani, R., Bien, J., Friedman, J., Hastie, T., Simon, N., Taylor, J., and Tibshirani, R. (2012). “Strong Rules for Discarding Predictors in Lasso-Type Problems.” Journal of the Royal Statistical Society, Series B 74:245–266.

Time Inc. (1987). “What They Make.” Sports Illustrated (April 20): 54–81.

Wang, J., Zhou, J., Wonka, P., and Ye, J. (2013). “Lasso Screening Rules via Dual Polytope Projection.” In Advances in Neural Information Processing Systems 26, edited by C. J. C. Burges, L. Bottou, M. Welling, Z. Ghahramani, and K. Q. Weinberger, 1070–1078. La Jolla, CA: Neural Information Processing Systems Foundation.

Xiang, Z. J., Xu, H., and Ramadge, P. J. (2011). “Learning Sparse Representations of High Dimensional Data on Large Scale Dictionaries.” In Advances in Neural Information Processing Systems 24, edited by J. Shawe-Taylor, R. S. Zemel, P. Bartlett, F. C. N. Pereira, and K. Q. Weinberger, 900–908. La Jolla, CA: Neural Information Processing Systems Foundation.

Yuan, M., and Lin, L. (2006). “Model Selection and Estimation in Regression with Grouped Variables.” Journal of the Royal Statistical Society, Series B 68:49–67.

Zou, H. (2006). “The Adaptive Lasso and Its Oracle Properties.” Journal of the American Statistical Association 101:1418–1429.

Zou, H., and Hastie, T. (2005). “Regularization and Variable Selection via the Elastic Net.” Journal of the Royal Statistical Society, Series B 67:301–320.