The GLMSELECT Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Model-Selection MethodsModel Selection IssuesCriteria Used in Model Selection MethodsCLASS Variable Parameterization and the SPLIT OptionMacro Variables Containing Selected ModelsUsing the STORE StatementBuilding the SSCP MatrixModel AveragingUsing Validation and Test DataCross ValidationExternal Cross ValidationScreeningDisplayed OutputODS Table NamesODS Graphics
Model-Selection MethodsModel Selection IssuesCriteria Used in Model Selection MethodsCLASS Variable Parameterization and the SPLIT OptionMacro Variables Containing Selected ModelsUsing the STORE StatementBuilding the SSCP MatrixModel AveragingUsing Validation and Test DataCross ValidationExternal Cross ValidationScreeningDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Group LASSO Selection (GROUPLASSO)
The group LASSO method proposed by Yuan and Lin (2006) is a variant of LASSO that is specifically designed for linear models defined in terms of effects that have multiple degrees of freedom, such as the main effects of CLASS variables, interactions between CLASS variables, and effects defined using an EFFECT statement.
Recall that LASSO selection depends on solving a constrained least squares problem of the form
![\[ \min ||\mb{y}-\bX \bbeta ||^2 \qquad \mbox{subject to} \quad \sum _{j=1}^{m} | \beta _ j | \leq t \]](images/statug_glmselect0031.png)
In this formulation, you can include or exclude individual parameters from the model independently, subject only to the overall
constraint. In contrast, the group LASSO method uses a constraint that forces all parameters that correspond to the same effect
to be included or excluded simultaneously. For a model that has k effects, let 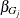 be the group of linear coefficients that correspond to effect j in the model. Then group LASSO depends on solving a constrained optimization problem of the form
be the group of linear coefficients that correspond to effect j in the model. Then group LASSO depends on solving a constrained optimization problem of the form
![\[ \min ||\mb{y}-\bX \bbeta ||^2 \qquad \mbox{subject to} \quad \sum _{j=1}^{k} \sqrt {|G_ j|} ||\beta _{G_ j}|| \leq t \]](images/statug_glmselect0055.png)
where 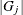 is the number of parameters that correspond to effect j, and
is the number of parameters that correspond to effect j, and 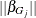 denotes the Euclidean norm of the parameters
denotes the Euclidean norm of the parameters 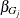 . That is, instead of constraining the sum of the absolute value of individual parameters, group LASSO constrains the Euclidean
norm of groups of parameters, where groups are defined by effects.
. That is, instead of constraining the sum of the absolute value of individual parameters, group LASSO constrains the Euclidean
norm of groups of parameters, where groups are defined by effects.
You can write the group LASSO method in the equivalent Lagrangian form
![\[ \min ||\mb{y}-\bX \bbeta ||^2 + \lambda \sum _{j=1}^{k} \sqrt {|G_ j|} ||\beta _{G_ j} || \]](images/statug_glmselect0058.png)
The weight 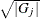 , as suggested by Yuan and Lin (2006), should take the size of the group into consideration in group LASSO.
, as suggested by Yuan and Lin (2006), should take the size of the group into consideration in group LASSO.
Unlike LASSO, group LASSO does not allow a piecewise linear constant solution path as generated by a LAR algorithm. Instead,
the method that Nesterov (2013) proposes is adopted to solve the Lagrangian form of the group LASSO problem that corresponds to a prespecified regularization
parameter, 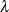 . Nesterov’s method is known to have an optimal convergence rate for first-order black box optimization. Because the optimal
. Nesterov’s method is known to have an optimal convergence rate for first-order black box optimization. Because the optimal
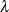 is usually unknown, a sequence of regularization parameters,
is usually unknown, a sequence of regularization parameters, 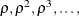 is employed, where
is employed, where 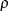 is a positive value less than 1. You can specify
is a positive value less than 1. You can specify 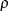 by using the RHO= suboption of the SELECTION=
option in the MODEL
statement; by default, RHO=0.9. In the ith step of group LASSO selection, the value used for
by using the RHO= suboption of the SELECTION=
option in the MODEL
statement; by default, RHO=0.9. In the ith step of group LASSO selection, the value used for 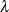 is
is 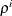 . If you want the solution that corresponds to a prespecified
. If you want the solution that corresponds to a prespecified 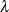 , you can specify the value of
, you can specify the value of 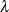 by using the L1= option together with STOP=L1.
by using the L1= option together with STOP=L1.
Another unique feature of the group LASSO method is that it does not necessarily add or remove precisely one effect at each step of the process. This is different from the forward, stepwise, backward, LAR, LASSO, and elastic net selection methods.