The GLMSELECT Procedure
-
Overview
- Getting Started
-
Syntax
-
DetailsModel-Selection MethodsModel Selection IssuesCriteria Used in Model Selection MethodsCLASS Variable Parameterization and the SPLIT OptionMacro Variables Containing Selected ModelsUsing the STORE StatementBuilding the SSCP MatrixModel AveragingUsing Validation and Test DataCross ValidationExternal Cross ValidationScreeningDisplayed OutputODS Table NamesODS Graphics
-
Examples
- References
Adaptive LASSO Selection
Adaptive LASSO selection is a modification of LASSO selection; in adaptive LASSO selection, weights are applied to each of
the parameters in forming the LASSO constraint (Zou 2006). More precisely, suppose that the response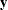 
has mean zero and the regressors 
are scaled to have mean zero and common standard deviation. Furthermore, suppose you can find a suitable estimator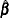 
of the parameters in the true model and you define a weight vector by 
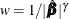, where 
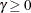. Then the adaptive LASSO regression coefficients 
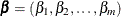are the solution to the constrained optimization problem
![\[ \min ||\mb{y}-\bX \bbeta ||^2 \qquad \mbox{subject to} \quad \sum _{j=1}^{m} | w_ j\beta _ j | \leq t \]](images/statug_glmselect0036.png)
You can specify 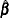by using the INEST=suboption of the SELECTION=LASSO option in the MODEL statement. The INEST= data set has the same structure
as the OUTEST= data set that is produced by several SAS/STAT procedures, including the REG and LOGISTIC procedures. The INEST=
data set must contain all explanatory variables in the MODEL
statement. It must also contain an intercept variable named Intercept unless you specify the NOINT option in the MODEL statement. If BY processing is used, the INEST= data set must also include
the BY variables, and there must be one observation for each BY group. If the INEST= data set also contains the _TYPE_ variable, only observations whose _TYPE_ value is PARMS are used.
If you do not specify an INEST= data set, then PROC GLMSELECT uses the solution to the unconstrained least squares problem
as the estimator 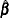. This is appropriate unless collinearity is a concern. If the regressors are collinear or nearly collinear, then Zou (2006) suggests using a ridge regression estimate to form the adaptive weights.