The FASTCLUS Procedure
Background
The FASTCLUS procedure combines an effective method for finding initial clusters with a standard iterative algorithm for minimizing the sum of squared distances from the cluster means. The result is an efficient procedure for disjoint clustering of large data sets. PROC FASTCLUS was directly inspired by the Hartigan (1975) leader algorithm and the MacQueen (1967) k-means algorithm. PROC FASTCLUS uses a method that Anderberg (1973) calls nearest centroid sorting. A set of points called cluster seeds is selected as a first guess of the means of the clusters. Each observation is assigned to the nearest seed to form temporary clusters. The seeds are then replaced by the means of the temporary clusters, and the process is repeated until no further changes occur in the clusters. Similar techniques are described in most references on clustering (Anderberg 1973; Hartigan 1975; Everitt 1980; Spath 1980).
The FASTCLUS procedure differs from other nearest centroid sorting methods in the way the initial cluster seeds are selected. The importance of initial seed selection is demonstrated by Milligan (1980).
The clustering is done on the basis of Euclidean distances computed from one or more numeric variables. If there are missing values, PROC FASTCLUS computes an adjusted distance by using the nonmissing values. Observations that are very close to each other are usually assigned to the same cluster, while observations that are far apart are in different clusters.
The FASTCLUS procedure operates in four steps:
-
Observations called cluster seeds are selected.
-
If you specify the DRIFT option, temporary clusters are formed by assigning each observation to the cluster with the nearest seed. Each time an observation is assigned, the cluster seed is updated as the current mean of the cluster. This method is sometimes called incremental, on-line, or adaptive training.
-
If the maximum number of iterations is greater than zero, clusters are formed by assigning each observation to the nearest seed. After all observations are assigned, the cluster seeds are replaced by either the cluster means or other location estimates (cluster centers) appropriate to the LEAST=p option. This step can be repeated until the changes in the cluster seeds become small or zero (MAXITER=
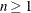 ).
).
-
Final clusters are formed by assigning each observation to the nearest seed.
If PROC FASTCLUS runs to complete convergence, the final cluster seeds will equal the cluster means or cluster centers. If PROC FASTCLUS terminates before complete convergence, which often happens with the default settings, the final cluster seeds might not equal the cluster means or cluster centers. If you want complete convergence, specify CONVERGE=0 and a large value for the MAXITER= option.
The initial cluster seeds must be observations with no missing values. You can specify the maximum number of seeds (and, hence, clusters) by using the MAXCLUSTERS= option. You can also specify a minimum distance by which the seeds must be separated by using the RADIUS= option.
PROC FASTCLUS always selects the first complete (no missing values) observation as the first seed. The next complete observation that is separated from the first seed by at least the distance specified in the RADIUS= option becomes the second seed. Later observations are selected as new seeds if they are separated from all previous seeds by at least the radius, as long as the maximum number of seeds is not exceeded.
If an observation is complete but fails to qualify as a new seed, PROC FASTCLUS considers using it to replace one of the old seeds. Two tests are made to see if the observation can qualify as a new seed.
First, an old seed is replaced if the distance between the observation and the closest seed is greater than the minimum distance between seeds. The seed that is replaced is selected from the two seeds that are closest to each other. The seed that is replaced is the one of these two with the shortest distance to the closest of the remaining seeds when the other seed is replaced by the current observation.
If the observation fails the first test for seed replacement, a second test is made. The observation replaces the nearest seed if the smallest distance from the observation to all seeds other than the nearest one is greater than the shortest distance from the nearest seed to all other seeds. If the observation fails this test, PROC FASTCLUS goes on to the next observation.
You can specify the REPLACE= option to limit seed replacement. You can omit the second test for seed replacement (REPLACE=PART), causing PROC FASTCLUS to run faster, but the seeds selected might not be as widely separated as those obtained by the default method. You can also suppress seed replacement entirely by specifying REPLACE=NONE. In this case, PROC FASTCLUS runs much faster, but you must choose a good value for the RADIUS= option in order to get good clusters. This method is similar to the Hartigan (1975, pp. 74–78) leader algorithm and the simple cluster seeking algorithm described by Tou and Gonzalez (1974, pp. 90–92).
