The FACTOR Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Input Data SetOutput Data SetsConfidence Intervals and the Salience of Factor LoadingsSimplicity Functions for RotationsMissing ValuesCautionsFactor ScoresVariable Weights and Variance ExplainedHeywood Cases and Other Anomalies about Communality EstimatesTime RequirementsDisplayed OutputODS Table NamesODS Graphics
Input Data SetOutput Data SetsConfidence Intervals and the Salience of Factor LoadingsSimplicity Functions for RotationsMissing ValuesCautionsFactor ScoresVariable Weights and Variance ExplainedHeywood Cases and Other Anomalies about Communality EstimatesTime RequirementsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
Example 37.1 Principal Component Analysis
This example analyzes socioeconomic data provided by Harman (1976). The five variables represent total population (Population), median school years (School), total employment (Employment), miscellaneous professional services (Services), and median house value (HouseValue). Each observation represents one of twelve census tracts in the Los Angeles Standard Metropolitan Statistical Area.
You conduct a principal component analysis by using the following statements:
data SocioEconomics; input Population School Employment Services HouseValue; datalines; 5700 12.8 2500 270 25000 1000 10.9 600 10 10000 3400 8.8 1000 10 9000 3800 13.6 1700 140 25000 4000 12.8 1600 140 25000 8200 8.3 2600 60 12000 1200 11.4 400 10 16000 9100 11.5 3300 60 14000 9900 12.5 3400 180 18000 9600 13.7 3600 390 25000 9600 9.6 3300 80 12000 9400 11.4 4000 100 13000 ;
proc factor data=SocioEconomics simple corr; run;
You begin with the specification of the raw data set with 12 observations. Then you use the DATA= option in the PROC FACTOR statement to specify the data set in the analysis. You also set the SIMPLE and CORR options for additional output results, which are shown in Output 37.1.2 and Output 37.1.3, respectively.
By default, PROC FACTOR assumes that all initial communalities are 1, which is the case for the current principal component analysis. If you intend to find common factors instead, use the PRIORS= option or the PRIORS statement to set initial communalities to values less than 1, which results in extracting the principal factors rather than the principal components. See Example 37.2 for the specification of a principal factor analysis.
For the current principal component analysis, the first output table is displayed in the Output 37.1.1.
Output 37.1.1: Principal Component Analysis: Number of Observations
In Output 37.1.1, the input data type is shown to be raw data. PROC FACTOR also accepts other data type such as correlations and covariances.
See Example 37.4 for the use of correlations as input data. For the current raw data set, PROC FACTOR reads in 12 records and all these 12
records are used. When there are missing values in the data set, these two numbers might not match due to the dropping of
the records with missing values. The last row of the table shows that 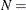 12 is used in the significance tests conducted in the analysis.
12 is used in the significance tests conducted in the analysis.
The SIMPLE option specified in the PROC FACTOR statement generates the means and standard deviations of all observed variables in the analysis, as shown in Output 37.1.2.
Output 37.1.2: Principal Component Analysis: Simple Statistics
The ranges of means and standard deviations for the analysis are quite large. Variables are measured on quite different scales. However, this is not an issue because PROC FACTOR basically analyzes the standardized scales (that is, the correlations) of the variables.
The CORR option specified in the PROC FACTOR statement generates the output of the observed correlations in Output 37.1.3.
Output 37.1.3: Principal Component Analysis: Correlations
| Correlations | |||||
|---|---|---|---|---|---|
| Population | School | Employment | Services | HouseValue | |
| Population | 1.00000 | 0.00975 | 0.97245 | 0.43887 | 0.02241 |
| School | 0.00975 | 1.00000 | 0.15428 | 0.69141 | 0.86307 |
| Employment | 0.97245 | 0.15428 | 1.00000 | 0.51472 | 0.12193 |
| Services | 0.43887 | 0.69141 | 0.51472 | 1.00000 | 0.77765 |
| HouseValue | 0.02241 | 0.86307 | 0.12193 | 0.77765 | 1.00000 |
The correlation matrix shown in Output 37.1.3 is analyzed by PROC FACTOR.
The first step of principal component analysis is to look at the eigenvalues of the correlation matrix. The larger eigenvalues are extracted first. Because there are five observed variables, five eigenvalues can be extracted, as shown in Output 37.1.4.
Output 37.1.4: Principal Component Analysis: Eigenvalues
In Output 37.1.4, the two largest eigenvalues are 2.8733 and 1.7967, which together account for 93.4% of the standardized variance. Thus, the first two principal components provide an adequate summary of the data for most purposes. Three components, which explain 97.7% of the variation, should be sufficient for almost any application. PROC FACTOR retains the first two components on the basis of the eigenvalues-greater-than-one rule since the third eigenvalue is only 0.2148.
To express the observed variables as functions of the components (or factors, in general), you consult the factor loading matrix as shown in Output 37.1.5.
Output 37.1.5: Principal Component Analysis: Factor Pattern
The factor pattern is often referred to as the factor loading matrix in factor analysis. The elements in the loading matrix are called factor loadings. There are at least two ways you can interpret these factor loadings. First, you can use this table to express the observed variables as functions of the extracted factors (or components, as in the current analysis). Each row of the factor loadings tells you the linear combination of the factor or component scores that would yield the expected value of the associated variable. Second, you can interpret each loading as a correlation between an observed variable and a factor or component, provided that the factor solution is an orthogonal one (that is, factors are uncorrelated), such as the current initial factor solution. Hence, the factor loadings indicate how strongly the variables and the factors or components are related.
In Output 37.1.5, the first component (labeled "Factor1") has large positive loadings for all five variables. Its correlation with Services (0.9324) is especially high. The second component is basically a contrast of Population (0.8064) and Employment (0.7261) against School (–0.5448) and HouseValue (–0.5582), with a very small loading on Services (–0.1043).
The total variance explained by the two components are shown in Output 37.1.6.
Output 37.1.6: Principal Component Analysis: Total Variance Explained by Factors
The first and second component account for 2.8733 and 1.7967, respectively, of the total variance of 5. In the initial factor solution, the total variance explained by the factors or components are the same as the eigenvalues extracted. (Compare the total variance with the eigenvalues shown in Output 37.1.4.) Due to the dropping of the less important components, the sum of these two numbers is 4.6700, which is only a little bit less than total variance 5 of the original correlation matrix.
You can also look at the variance explained by the two components for each observed variables in Output 37.1.7.
Output 37.1.7: Principal Component Analysis: Final Communality Estimates
In Output 37.1.7, the final communality estimates show that all the variables are well accounted for by the two components, with final communality
estimates ranging from 0.8802 for Services to 0.9878 for Population. The sum of the communalities is 4.6700, which is the same as the sum of the variance explained by the two components, as
shown in Output 37.1.6.
Principal Component Analysis by PROC FACTOR and PROC PRINCOMP
The principal component analysis by PROC FACTOR emphasizes how the principal components explain the observed variables. The
factor loadings in the factor pattern as shown in Output 37.1.5 are the coefficients for combining the factor/component scores to yield the observed variable scores when the expected error
residuals are zero. For example, the predicted standardized value of Population given the factor/component scores for Factor1 and Factor2 is given by:
![\[ \Variable{Population} = 0.58096 \times \Variable{Factor1} + 0.80642 \times \Variable{Factor2} \]](images/statug_factor0081.png)
If you are primarily interested in getting the component scores as linear combinations of the observed variables, the factor loading matrix table is not the right one for you. However, you might request the standardized scoring coefficients by adding the SCORE option in the FACTOR statement:
proc factor data=SocioEconomics n=5 score; run;
In the preceding PROC FACTOR statement, N=5 is specified for retaining all five components. This is done for comparing the PROC FACTOR results with those of PROC PRINCOMP, which is described later. The SCORE option requests the display of the standardized scoring coefficients, which are shown in Output 37.1.8.
Output 37.1.8: Principal Component Analysis: Scoring Coefficients for Computing Component Scores
| Standardized Scoring Coefficients | |||||
|---|---|---|---|---|---|
| Factor1 | Factor2 | Factor3 | Factor4 | Factor5 | |
| Population | 0.20219065 | 0.44884459 | 0.1284067 | 0.64542101 | 5.58240225 |
| School | 0.26695219 | -0.3032049 | 1.48611655 | -1.1184573 | 1.41573501 |
| Employment | 0.23402646 | 0.40410834 | 0.53496241 | 0.07255759 | -5.6513542 |
| Services | 0.32450082 | -0.0580552 | -1.432726 | -1.5828806 | -0.0010006 |
| HouseValue | 0.27534803 | -0.3106762 | -0.3012889 | 2.41418899 | -0.6673445 |
In Output 37.1.8, each factor/component is expressed as a linear combination of the standardized observed variables. For example, the first
principal component or Factor1 is computed as:
![\[ 0.2022 \times \Variable{Population} + 0.2670 \times \Variable{School} + 0.2340 \times \Variable{Employment} + 0.3245 \times \Variable{Services} + 0.2753 \times \Variable{HouseValue} \]](images/statug_factor0082.png)
Again, when applying this formula you must use the standardized observed variables (with means 0 and standard deviations 1), but not the raw data.
Apart from some scaling differences, the set of scoring coefficients obtained from PROC FACTOR are equivalent to those obtained from PROC PRINCOMP, as specified by the following statement:
proc princomp data=SocioEconomics; run;
PROC PRINCOMP displays the scoring coefficients as eigenvectors, which are shown in Output 37.1.9.
Output 37.1.9: Principal Component Analysis by PROC PRINCOMP: Eigenvectors
| Eigenvectors | |||||
|---|---|---|---|---|---|
| Prin1 | Prin2 | Prin3 | Prin4 | Prin5 | |
| Population | 0.342730 | 0.601629 | 0.059517 | 0.204033 | 0.689497 |
| School | 0.452507 | -.406414 | 0.688822 | -.353571 | 0.174861 |
| Employment | 0.396695 | 0.541665 | 0.247958 | 0.022937 | -.698014 |
| Services | 0.550057 | -.077817 | -.664076 | -.500386 | -.000124 |
| HouseValue | 0.466738 | -.416429 | -.139649 | 0.763182 | -.082425 |
For example, to get the first principal component score, you use the following formula:
![\[ 0.3427 \times {\Variable{Population}} + 0.4525 \times {\Variable{School}} + 0.3967 \times {\Variable{Employment}} + 0.5500 \times {\Variable{Services}} + 0.4667 \times {\Variable{HouseValue}} \]](images/statug_factor0083.png)
This formula is not exactly the same as the one shown by using PROC FACTOR. All scoring coefficients in PROC FACTOR are smaller, approximately a factor of 0.59 to those coefficients obtained from PROC PRINCOMP. The reason for the scalar difference is that PROC FACTOR assumes all factors/components to have variance of 1, while PROC PRINCOMP creates components that have variances equal to the eigenvalues. You can do a simple rescaling of the standardized scoring coefficients obtained from PROC FACTOR so that they match the associated eigenvectors from the PROC PRINCOMP. Basically, you need to rescale each column of the standardized scoring coefficients obtained from PROC FACTOR to have the sum of squares equaling one, which is a defining characteristic of eigenvectors. This could be accomplished by dividing each coefficient by the square root of the corresponding column sum of squares.
For the present example, you can use PROC STDIZE to do the rescaling, as shown in the following statements:
proc factor data=SocioEconomics n=5 score; ods output StdScoreCoef=Coef; run; proc stdize method=ustd mult=.44721 data=Coef out=eigenvectors; var Factor1-Factor5; run; proc print data=eigenvectors; run;
First, you create an output set Coef for the standardized scoring coefficients by the ODS OUTPUT statement. Note that "StdScoreCoef" is the ODS table that contains
the standardized scoring coefficients as shown in Output 37.1.8. (See Table 37.6 for all ODS table names for PROC FACTOR.) Next, you use METHOD=USTD in the PROC STDIZE statement to divide the output coefficients
by the corresponding uncorrected (for mean) standard deviations. The following formula shows the relationship between the
uncorrected standard deviation and the sum of squares:
![\[ \mbox{uncorrected standard deviation} = \sqrt {\mbox{sum of squares}/N} \]](images/statug_factor0084.png)
Recall that what you intend to divide from each coefficient is its square root of the corresponding column sum of squares.
Therefore, to adjust for what PROC STDIZE does using METHOD=USTD, you have to multiply each variable by a constant term of
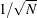 in the standardization. For the current example, this constant term is 0.44721 (
in the standardization. For the current example, this constant term is 0.44721 (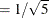 ) and is specified through the MULT= option in the PROC STDIZE statement. With the OUT= option, the rescaled scoring coefficients
are saved in the SAS data set
) and is specified through the MULT= option in the PROC STDIZE statement. With the OUT= option, the rescaled scoring coefficients
are saved in the SAS data set eigenvectors. The printout of the data set in Output 37.1.10 shows the rescaled standardized scoring coefficients obtained from PROC FACTOR.
Output 37.1.10: Rescaled Standardized Scoring Coefficients
| Obs | Variable | Factor1 | Factor2 | Factor3 | Factor4 | Factor5 |
|---|---|---|---|---|---|---|
| 1 | Population | 0.34272761 | 0.60162443 | 0.05951667 | 0.20403109 | 0.68949172 |
| 2 | School | 0.45250304 | -0.4064112 | 0.68881691 | -0.3535678 | 0.17485977 |
| 3 | Employment | 0.39669158 | 0.54166065 | 0.24795576 | 0.02293697 | -0.6980081 |
| 4 | Services | 0.5500521 | -0.0778162 | -0.6640703 | -0.5003817 | -0.0001236 |
| 5 | HouseValue | 0.4667346 | -0.4164256 | -0.1396478 | 0.76317568 | -0.0824248 |
As you can see, these standardized scoring coefficients are essentially the same as those obtained from PROC PRINCOMP, as shown in Output 37.1.9. This example shows that principal component analyses by PROC FACTOR and PROC PRINCOMP are indeed equivalent. PROC PRINCOMP emphasizes more the linear combinations of the variables to form the components, while PROC FACTOR expresses variables as linear combinations of the components in the output. If a principal component analysis of the data is all you need in a particular application, there is no reason to use PROC FACTOR instead of PROC PRINCOMP. Therefore, the following examples focus on common factor analysis for which that you can apply only PROC FACTOR, but not PROC PRINCOMP.