The VARIOGRAM Procedure
The VARIOGRAM procedure produces a fit summary table to report about the goodness of fit. When you specify multiple models to fit with the FORM=AUTO option in the MODEL statement, the VARIOGRAM procedure uses two processes to rank the fitted models: The first one depends on your choice among available fitting criteria. The second one is based on an operational classification of equivalent models in classes. The two processes are described in more detail in the following subsections.
Overall, no absolutely correct way exists to rank and classify multiple models. Your choice of ranking criteria could depend on your study specifications, physical considerations, or even your personal assessment of fitting performance. The VARIOGRAM procedure provides you with fitting and comparison features to facilitate and help you better understand the fitting process.
The fit summary table ranks multiple models on the basis of one or more fitting criteria that you can specify with the CHOOSE= option of the MODEL statement, as explained in the section Syntax: VARIOGRAM Procedure. Currently, the VARIOGRAM procedure offers two numerical criteria (for which a smaller value indicates a better fit) and a qualitative criterion:
-
The residual sum of squares error (SSE) is based on the objective function of the fitting process. When the specified method is weighted least squares, the sum of squares of the weighted differences (WSSE) is computed according to the expression
![\[ \mr{WSSE} = \sum _{i=1}^ k {w_ i}^2 \left[\gamma ^\ast _ z(\bm {h}_ i) - \gamma _{z}(\bm {h}_ i;\bm {\theta }) \right]^2 \]](images/statug_variogram0235.png)
where
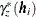 can be either the classical or robust semivariance estimate of the theoretical semivariance
can be either the classical or robust semivariance estimate of the theoretical semivariance 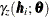 at the ith lag and the weights
at the ith lag and the weights 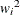 are taken at lags
are taken at lags 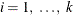 . When you specify the METHOD=OLS
option in the MODEL
, the weights
. When you specify the METHOD=OLS
option in the MODEL
, the weights 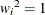 for
for 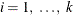 , and the SSE is expressed as
, and the SSE is expressed as
![\[ \mr{SSE} = \sum _{i=1}^ k \left[\gamma ^\ast _ z(\bm {h}_ i) - \gamma _{z}(\bm {h}_ i;\bm {\theta }) \right]^2 \]](images/statug_variogram0239.png)
-
Akaike’s information criterion (AIC) is included in the fit summary table when there is at least one nonfixed parameter. In its strict definition, AIC assumes that the model errors are normally and independently distributed. This assumption is not correct in the semivariance fitting analysis. However, the AIC can be also defined in an operational manner on the basis of the weighted squared error sum WSSE as
![\[ \mr{AIC} = k \mr{ln}\left( \frac{ \mr{WSSE} }{ k } \right) + 2 q \]](images/statug_variogram0240.png)
for k lags and q model parameters; see, for example, Olea (1999, p. 84). The operational definition of the AIC is provided as an additional criterion for the comparison of fitted models in PROC VARIOGRAM.
The AIC expression suggests that when you specify multiple models with the FORM=AUTO option in the MODEL statement, all models with the same number of parameters are ranked in the same way by the AIC and the WSSE criteria. Among models with the same WSSE value, AIC ranks higher the ones with fewer parameters.
-
The third qualitative criterion enables you to classify multiple models based on their convergence status. A model is sent to the bottom of the ranking table if the parameter estimation optimization fails to converge or fitting is unsuccessful due to any other issue. These two cases are distinguished by the different notes they produce in the fit summary ODS table. If you specify the STORE statement to save the fitting output in an item store, then models that have failed to fit are not passed to the item store.
With respect to convergence status, PROC VARIOGRAM ranks higher those models that have successfully completed the fitting process. It might occur that the selection of parameter initial values, physical considerations about the forms that are used for the fit, or numerical aspects of the nonlinear optimization could result in ambiguous fits. For example, you might see that model parameters converge at or near their boundary values, or that parameters have unreasonably high estimates when compared to the empirical semivariogram characteristics. Then, the fit summary table designates such fits as questionable.
You might not need to take any action if you are satisfied with the fitting results and the selected model. You can investigate questionable fits in one or more of the following ways:
-
If a form in a nested model makes no contribution to the model due to a parameter at or near its boundary value, then you could have a case of a degenerate fit. When you fit multiple models, a model with degenerate fit can collapse to the more simple model that does not include the noncontributing form. The VARIOGRAM procedure includes in its fit summary all models that are successfully fit. In such cases you can ignore degenerate fits. You can also try subsequent fits of individual models and exclude noncontributing forms or use different initial values.
-
Unreasonably low or high parameter estimates might be an indication that the current initial values are not a good guess for the nonlinear optimizer. In most cases, fitting an empirical semivariogram gives you the advantage of a fair understanding about the value range of your parameters. Then, you can use the PARMS statement to specify a different set of initial values and try the fit again.
-
Try replacing the problematic form with another one. A clear example is that you can expect a very poor fit if you specify an exponential model to fit an empirical semivariogram that suggests linear behavior.
Eventually, if none of the aforementioned issues exist, then a model is ranked in the highest positions of the fit summary table. You can combine two or more of the fitting criteria to manage classification of multiple fitted models in a more detailed manner.
In some cases you might still experience a poor quality of fit or no fit at all. If none of the earlier suggestions results in a satisfactory fit, then you could decide to re-estimate the empirical semivariogram for your same input data. The following actions can produce different empirical semivariograms to fit a theoretical model to:
-
If you compute the semivariogram for different angles and you experience optimization failures, try specifying explicitly the same direction angles with different tolerance or bandwidth value in the DIRECTIONS statement.
-
Modify slightly the LAGDISTANCE= option in the COMPUTE statement to obtain a different empirical semivariogram.
Finally, it is possible to have models in the fitting summary table ranked in a way that seemingly contradicts the specification in the CHOOSE= option of the MODEL statement. Consider an example with the default behavior CHOOSE= (SSE AIC), where you might observe that models have the same SSE values but are not ranked further as expected by the AIC criterion. A closer examination of such cases typically reduces this issue to a matter of the accuracy shown in the table. That is, the displayed accuracy of the SSE values might hide additional decimal digits that justify the given ranking.
In such scenarios, discrimination of models at the limits of numerical accuracy might suggest that you choose a model of questionable fit or a nested structure over a more simple one. You can then review the candidate models and exercise your judgment to select the model that works best for you. If all values of a criterion are equal, then the ranking order is simply the order in which models are examined unless more criteria follow that can affect the ranking.
The fit summary that is produced after fitting multiple models further categorizes the ranked models in classes of equivalence. Equivalence classification is an additional investigation that is unrelated to the ranking criteria presented in the previous subsection; it is an operational criterion that provides you with a qualitative overview of multiple model fit performance under given fitting conditions.
To examine model equivalence, the VARIOGRAM procedure computes the semivariances for each one of the fitted models at a set of distances. For any pair of consecutively ranked models, if the sum of their semivariance absolute differences at all designated distances is smaller than the tolerance specified by the EQUIVTOL= parameter, then the two models are deemed equivalent and placed in the same class; otherwise, they are placed in different classes. Equivalence classification depends on the existing ranking; hence the resulting classes can differ when you specify different ranking criteria in the CHOOSE= option of the MODEL statement.
The equivalence class numbers start at 1 for the top-ranked model in the fit summary table. You can consider the top model of each equivalence class to be a representative of the class behavior. When you specify that fit plots be produced and there are equivalence classes, the plot displays the equivalence classes and the legend designates each one by its representative model.
Consequently, if an equivalence class contains multiple members after a fit, then all of its members produce in general the exact same semivariogram. A typical reason could be that the fitting process estimates of scale parameters are at or close to their zero boundaries in one or more nested forms in a model. In such cases, the behavior of this model reduces to the behavior of its nested components with nonzero parameters. When one or more models share this situation or have the same contributing nested forms, they could end up as members of the same equivalence class depending on the ranking criteria.
It is not necessary for all models in the same equivalence class to produce the exact same semivariogram. If a fit of two obviously different forms involves semivariance values that are small enough for the equivalence criterion to be satisfied by the default value of the EQUIVTOL= option, then you might need to specify an even smaller value in the EQUIVTOL= option to rank these two models in separate equivalence classes.
