The KRIGE2D Procedure
The example in the section Aspects of Semivariogram Model Fitting in Chapter 109: The VARIOGRAM Procedure, investigates fitting of a theoretical model to describe spatial correlation in a study of 138 simulated arsenic logarithm
concentration (logAs) observations. These observations form the logAsData data set, which is treated as actual data for illustration in the examples.
In this example, you use the logAsData data set and the semivariogram analysis results to predict the logAs variable values across space in a specified square region of size 500 km ![]() 500 km. Your goal is to answer scientific questions in your analysis by means of your prediction results. This application
highlights the impact of the correlation model choice on predictions. The example in section Investigating the Effect of Model Specification on Spatial Prediction examines additional aspects of this impact.
500 km. Your goal is to answer scientific questions in your analysis by means of your prediction results. This application
highlights the impact of the correlation model choice on predictions. The example in section Investigating the Effect of Model Specification on Spatial Prediction examines additional aspects of this impact.
The World Health Organization (WHO) standard for maximum arsenic concentration in drinking water is 10 ![]() g/lt. Assume that you want to answer the following question: In what percentage of the study area does the Arsenic concentration
exceed the WHO regulatory standard?
g/lt. Assume that you want to answer the following question: In what percentage of the study area does the Arsenic concentration
exceed the WHO regulatory standard?
First, you read the logAsData data set with the following DATA step:
title 'Spatial Prediction of Log-Arsenic Concentration';
data logAsData;
input East North logAs @@;
label logAs='log(As) Concentration';
datalines;
193.0 296.6 -0.68153 232.6 479.1 0.96279 268.7 312.5 -1.02908
43.6 4.9 0.65010 152.6 54.9 1.87076 449.1 395.8 0.95932
310.9 493.6 -1.66208 287.8 164.9 -0.01779 330.0 8.0 2.06837
225.7 241.7 0.15899 452.3 83.4 -1.21217 156.5 462.5 -0.89031
11.5 84.4 -0.24496 144.4 335.7 0.11950 149.0 431.8 -0.57251
234.3 123.2 -1.33642 37.8 197.8 -0.27624 183.1 173.9 -2.14558
149.3 426.7 -1.06506 434.4 67.5 -1.04657 439.6 237.0 -0.09074
36.4 175.2 -1.21211 370.6 244.0 3.28091 452.0 96.5 -0.77081
247.0 86.8 0.04720 413.6 373.2 1.78235 253.5 291.7 0.56132
129.7 111.9 1.34000 352.7 42.1 0.23621 279.3 82.7 2.12350
382.6 290.7 0.86756 188.2 222.8 -1.23308 382.8 154.5 -0.94094
304.4 309.2 -1.95158 337.5 387.2 -1.31294 490.7 189.8 0.40206
159.0 100.1 -0.22272 245.5 329.2 -0.26082 372.1 379.5 -1.89078
417.8 84.1 -1.25176 173.9 407.6 -0.24240 121.5 107.7 1.54509
453.5 313.6 0.65895 143.5 346.7 -0.87196 157.4 125.5 -1.96165
371.8 353.2 -0.59464 358.9 338.2 -1.07133 8.6 437.8 1.44203
395.9 394.2 -0.24144 149.5 58.9 1.17459 453.5 420.6 -0.63951
182.3 85.0 1.00005 21.0 290.1 0.31016 11.1 352.2 -0.88418
131.2 238.4 -0.57184 104.9 6.3 1.12054 247.3 256.0 0.14019
428.4 383.7 0.92448 327.8 481.1 -2.72543 199.2 92.8 -0.05717
453.9 230.1 0.16571 205.0 250.6 0.07581 459.5 271.6 0.93700
229.5 262.8 1.83590 370.4 228.6 2.96611 330.2 281.9 1.79723
354.8 388.3 -3.18262 406.2 222.7 2.41594 254.4 393.1 2.03221
96.7 85.2 -0.47156 407.2 256.8 0.66747 498.5 273.8 1.03041
417.2 471.4 -1.42766 368.8 424.3 -0.70506 303.0 59.1 1.43070
403.1 264.1 1.64554 21.2 360.8 0.67094 148.2 78.1 2.15323
305.5 310.7 -1.47985 228.5 180.3 -0.68386 161.1 143.3 1.07901
70.5 155.1 0.54652 363.1 282.6 -0.43051 86.0 472.5 -1.18855
175.9 105.3 -2.08112 96.8 426.3 1.56592 475.1 453.1 -1.53776
125.7 485.4 1.40054 277.9 201.6 -0.54565 406.2 125.0 -1.38657
60.0 275.5 -0.59966 431.3 494.6 -0.36860 399.9 399.0 -0.77265
28.8 311.1 0.91693 166.1 348.2 -0.49056 266.6 83.5 0.67277
54.7 356.3 0.49596 433.5 460.3 -1.61309 201.7 167.6 -1.40678
158.1 203.6 -1.32499 67.6 230.4 1.14672 81.9 250.0 0.63378
372.0 50.7 0.72445 26.4 264.6 1.00862 300.1 91.7 -0.74089
303.0 447.4 1.74589 108.4 386.2 1.12847 55.6 191.7 0.95175
36.3 273.2 1.78880 94.5 298.3 -2.43320 366.1 187.3 -0.80526
130.7 389.2 -0.31513 37.2 324.2 0.24489 295.5 211.8 0.41899
58.6 206.2 0.18495 346.3 142.8 -0.92038 484.2 215.9 0.08012
451.4 415.7 0.02773 58.9 86.5 0.17652 212.6 363.9 0.17215
378.7 407.6 0.51516 265.9 305.0 -0.30718 123.2 314.8 -0.90591
26.9 471.7 1.70285 16.5 7.1 0.51736 255.1 472.6 2.02381
111.5 148.4 -0.09658 440.4 375.0 1.23285 406.4 19.5 1.01181
321.2 65.8 -0.02095 466.4 357.1 -0.49272 2.0 484.6 0.50994
200.9 205.1 0.43543 30.3 337.0 1.60882 297.0 12.7 1.79824
158.2 450.7 0.05295 122.8 105.3 1.53936 417.8 329.7 -2.08124
;
For prediction of the logAs values in the specified area, assume a rectangular grid of nodes with an equal spacing of 5 km between neighboring nodes
in the north and east directions. This produces a total of ![]() prediction locations.
prediction locations.
In the section Aspects of Semivariogram Model Fitting in Chapter 109: The VARIOGRAM Procedure, you saved the selected fitted model that resulted from the correlation analysis into the SemivAsStore item store as shown in the following statements:
ods graphics on;
proc variogram data=logAsData plots=none; store out=SemivAsStore / label='LogAs Concentration Models'; compute lagd=5 maxlag=40; coord xc=East yc=North; model form=auto(mlist=(exp,gau,mat) nest=1 to 2); var logAs; run;
In the KRIGE2D procedure you specify the name of the item store you want to use for prediction input in the IN= option of the RESTORE statement. You request use of the selected model for prediction by specifying the STORESELECT option in the MODEL statement.
The INFO option of the RESTORE statement produces a table with information about the selected fitted model in the item store. To review all models in the input item store, specify the two INFO option suboptions. In particular, specify the DET suboption to request details about all additional fitted models that are included in the item store and the ONLY suboption to suppress prediction and produce only the tables about the item store, as shown in the following statements:
proc krige2d data=logAsData outest=pred plots=none; restore in=SemivAsStore / info(det only); coordinates xc=East yc=North; predict var=logAs; model storeselect; grid x=0 to 500 by 5 y=0 to 500 by 5; run;
PROC KRIGE2D produces a table with general information about the input item store identity, as shown in Output 55.1.1.
Output 55.1.1: PROC KRIGE2D and Input Item Store General Information
| Spatial Prediction of Log-Arsenic Concentration |
| Correlation Model Item Store Information | |
|---|---|
| Input Item Store | WORK.SEMIVASSTORE |
| Item Store Label | LogAs Concentration Models |
| Data Set Created From | WORK.LOGASDATA |
| By-group Information | No By-groups Present |
| Created By | PROC VARIOGRAM |
| Date Created | 15MAY14:14:01:10 |
The second table in Output 55.1.2 itemizes the variables in the item store and displays the sample mean and standard deviation of their data set of origin.
Hence, the values shown in Output 55.1.2 refer to the observations in the logAsData data set.
The table in Output 55.1.3 presents all the correlation models fitted to the arsenic logarithm logAs empirical semivariance that are saved in the SemivAsStore item store.
According to Output 55.1.3, the Gaussian-Gaussian model is the selected model for the empirical semivariance fit based on the specific weighted least
squares fit and ranking criteria. In the section Aspects of Semivariogram Model Fitting in Chapter 109: The VARIOGRAM Procedure, it is noted that all fitted models in the first five equivalence classes produce very similar semivariograms, and this is
likely to lead to similar results in prediction analysis. For comparison purposes, you choose to examine the selected model,
in addition to the exponential model in the SemivAsStore item store. As shown in Output 55.1.3, the exponential model is one of the least well-fit models based on the criteria used for the specific fit. You are interested
in comparing the predictions from each one of these two models, and you examine their impact on your analysis.
The default item store model selection is the model on top of the list in Output 55.1.3. Hence, you specify the STORESELECT
option in the MODEL
statement without any suboptions, and it invokes the Gaussian-Gaussian model from the SemivAsStore item store. You assign the label SELMODEL to the corresponding MODEL
statement.
You also specify a second MODEL statement with the label EXPMODEL to request prediction based on the exponential correlation form. In this case you specify the STORESELECT(MODEL=) option in the MODEL statement to request the desired form.
You omit the INFO
option from the RESTORE
statement. You specify the PRED
and the SEMIVAR
options in the PLOTS
option of the PROC KRIGE2D
statement to produce plots of the predicted values and the semivariance model, respectively, for each MODEL
statement. You request that the prediction output be saved in the Pred output data set.
You satisfy the preceding requests by specifying the following statements:
proc krige2d data=logAsData outest=Pred plots(only)=(pred semivar); restore in=SemivAsStore; coordinates xc=East yc=North; predict var=logAs; SelModel: model storeselect; ExpModel: model storeselect(model=exp); grid x=0 to 500 by 5 y=0 to 500 by 5; run;
When you run these statements, in addition to the input item store information table, PROC KRIGE2D also produces the number of observations table and general kriging process information, as shown in Output 55.1.4.
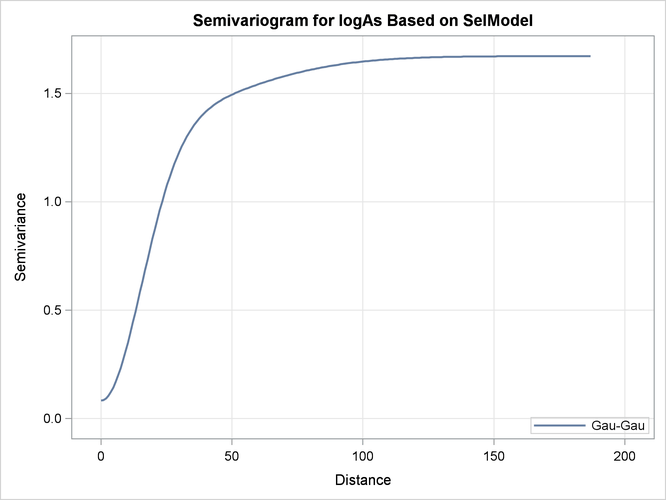
PROC KRIGE2D first uses the Gaussian-Gaussian model. The table in Output 55.1.5 shows the saved parameter values of the fitted Gaussian-Gaussian model in the SemivAsStore item store. PROC KRIGE2D uses these parameters for the prediction based on the selected model.
Output 55.1.5: Information about the Gaussian-Gaussian Model
| Spatial Prediction of Log-Arsenic Concentration |
| Covariance Model Information for SelModel | |
|---|---|
| Nested Structure 1 Type | Gaussian |
| Nested Structure 1 Sill | 0.3276646 |
| Nested Structure 1 Range | 62.312728 |
| Nested Structure 1 Effective Range | 107.92881 |
| Nested Structure 2 Type | Gaussian |
| Nested Structure 2 Sill | 1.261545 |
| Nested Structure 2 Range | 21.459563 |
| Nested Structure 2 Effective Range | 37.169053 |
| Nugget Effect | 0.0830758 |
The semivariogram of the Gaussian-Gaussian model with the parameters shown in Output 55.1.5 is depicted in Output 55.1.6.
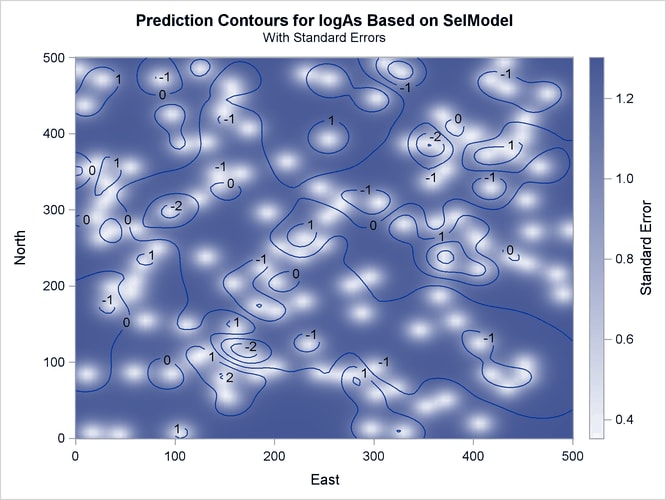
Output 55.1.7 is a map of the kriging prediction of the arsenic concentration values logAs in the specified domain. The prediction error surface shows a naturally increasing error as you move farther away from the
observation locations. Interestingly, kriging predicts a small area of increased arsenic concentration values located in the
central-eastern part of the domain. The WHO threshold of 10 ![]() g/lt for the maximum allowed arsenic concentration in water translates into about 2.3 in the log scale, and the particular
area exhibits values in excess of 3. Due to the suggested violation of the WHO standard, this particular area is very likely
to be the focus of further environmental risk analysis.
g/lt for the maximum allowed arsenic concentration in water translates into about 2.3 in the log scale, and the particular
area exhibits values in excess of 3. Due to the suggested violation of the WHO standard, this particular area is very likely
to be the focus of further environmental risk analysis.
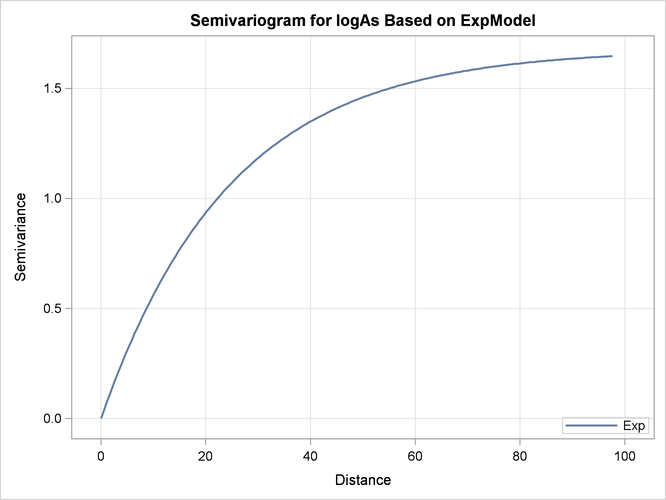
Next, PROC KRIGE2D performs prediction with the exponential model. The model parameters are also read from the SemivAsStore item store and are shown in Output 55.1.8.
Output 55.1.9 illustrates the semivariogram of the nested exponential model where its parameter values are those shown in Output 55.1.8.
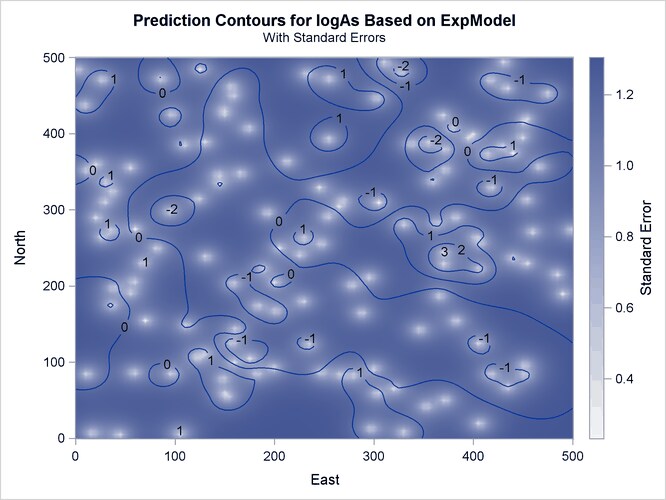
The prediction plot for the exponential model is shown in Output 55.1.10. Prediction values and spatial patterns are similar overall to those of the Gaussian-Gaussian case. Clearly, although both models predict the same basic characteristics for the arsenic logarithm concentration distribution, the exponential model suggests a more limited spatial variability in closely neighboring locations. The lack of a nugget effect in the exponential model justifies this behavior. Also, the exponential model predictions seem less inclined to deviate farther away from the near-zero mean than the Gaussian-Gaussian model predictions.The prediction error reaches about the same upper values for both models, though its low values are slightly smaller in the exponential model.
In the following two-step computation, you proceed to compute the percentage of the study area where the arsenic concentration
exceeds the WHO regulatory standard according to your predictions. First, a DATA step marks the arsenic predicted values in
excess of the WHO concentration threshold of 10 ![]() g/lt and saves the outcome into an indicator variable
g/lt and saves the outcome into an indicator variable OverLimit. The DATA step input is the prediction Pred output data set, where the logarithm arsenic prediction is stored in the estimate variable. The DATA step also transforms the arsenic logarithm values back into arsenic concentration values to compare them
to the threshold value. You use the following statements:
data AsOverLimit; set Pred; OverLimit = (exp(estimate) > 10) * 100; run;
The second step uses the MEANS procedure to express the selected nodes population, where the WHO arsenic concentration limit
violation occurs, as a percentage of the entire domain area. You study the results of each correlation model separately by
specifying the BY statement in the PROC MEANS. The BY variable is the Label variable in the AsOverLimit and Pred data sets. You need to sort the AsOverLimit data prior to using PROC MEANS. You run the following statements:
proc sort data=AsOverLimit; by Label; run; proc means data=AsOverLimit mean; var OverLimit; by label; label Overlimit="Percent above WHO threshold"; run; ods graphics off;
The Gaussian-Gaussian model prediction produces the result in Output 55.1.11. The analysis suggests a minimal occurrence of excessive arsenic concentration in drinking water in about 0.43% of the study region.
The exponential model predicts that the WHO arsenic concentration threshold is exceeded in about 0.27% of the domain, as shown in Output 55.1.12. Although this is still a minimal occurrence of the threshold violation across the region, the exponential model estimates the impact to be at about two thirds of the Gaussian-Gaussian model percentage.
The results in Output 55.1.11 and Output 55.1.12 suggest that it might not be possible to provide a unique answer about the area percentage that is affected by increased arsenic concentration. You chose to examine two different correlation models whose performance is relatively similar, and they provide impact estimates that differ by about 37%.
You might conclude that the answer to the initial question about the percentage value lies in the neighborhood of the results given by the two correlation models. Further analysis with more models is necessary to validate this assumption. It is important to note that apart from the continuity model choice, additional factors contribute to this investigation. Such factors could be the use of local instead of global kriging, or even going back to the empirical semivariogram computation stage and repeating the analysis for different possible spatial continuity empirical estimates. A sensible approach to tackle this analysis would be to investigate the range of the impact suggested by all candidate correlation models and to proceed by defining the best and worst case scenarios for the size of the affected area.
Eventually, when it comes to using your findings, it is important to account for the subjective nature of stochastic analysis and multiple possible answers to your questions. In that sense, some scientific questions might be more sensible than others to interpret your results correctly. For instance, you might want to investigate only whether the adversely affected domain percentage is below 1%, rather than attempting to provide a specific value for it. Then, you might consider the preceding findings sufficient, despite any fluctuations in the estimated percentage. In a different scenario, the areas with high pollutant concentration could be populated. Hence, any local health standard violation is probably unacceptable, and it can be crucial that you provide solid and more detailed assessment in that case.
The section Risk Analysis with Simulation in Chapter 91: The SIM2D Procedure, investigates a different aspect of this study and offers additional perspective about spatial analysis.