The HPMIXED Procedure
The RANDOM statement defines the random effects in the mixed model. It can be used to specify traditional variance component models (as in the VARCOMP procedure) and to specify random coefficients. The random effects can be classification or continuous. Multiple RANDOM statements are possible. Random effects specified in a RANDOM statement could be correlated with each other for certain types of covariance structures (see the TYPE= option). It is, however, assumed that random effects specified using different RANDOM statements are not correlated.
Using notation from the section Model Assumptions, the purpose of the RANDOM statement is to define the ![]() matrix of the mixed model, the random effects in the
matrix of the mixed model, the random effects in the ![]() vector, and the structure of
vector, and the structure of ![]() . The
. The ![]() matrix is constructed exactly like the
matrix is constructed exactly like the ![]() matrix for the fixed effects, and the
matrix for the fixed effects, and the ![]() matrix is constructed to correspond to the effects constituting
matrix is constructed to correspond to the effects constituting ![]() . The structure of
. The structure of ![]() is defined by using the TYPE=
option.
is defined by using the TYPE=
option.
You can specify INTERCEPT (or INT) as a random effect. PROC HPMIXED does not include the intercept in the RANDOM statement by default, as it does in the MODEL statement.
You can specify the following options in the RANDOM statement after a slash (/).
- ALPHA=number
-
requests that a t-type confidence interval with confidence level
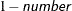 be constructed for the predictors of random effects in this statement. The value of number must be between 0 and 1 exclusively; the default is 0.05. Specifying the ALPHA= option implies the CL
option.
be constructed for the predictors of random effects in this statement. The value of number must be between 0 and 1 exclusively; the default is 0.05. Specifying the ALPHA= option implies the CL
option.
- CL
-
requests that t-type confidence limits be constructed for each of the predictors of random effects in this statement. The confidence level is 0.95 by default; this can be changed with the ALPHA= option. The CL option implies the SOLUTION option.
- GROUP=effect
-
defines an effect specifying heterogeneity in the covariance structure of
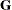 . All observations having the same level of the group effect have the same covariance parameters. Each new level of the group
effect produces a new set of covariance parameters with the same structure as the original group. You should exercise caution
in defining the group effect, because strange covariance patterns can result from its misuse. Also, the group effect can greatly
increase the number of estimated covariance parameters, which can adversely affect the optimization process.
. All observations having the same level of the group effect have the same covariance parameters. Each new level of the group
effect produces a new set of covariance parameters with the same structure as the original group. You should exercise caution
in defining the group effect, because strange covariance patterns can result from its misuse. Also, the group effect can greatly
increase the number of estimated covariance parameters, which can adversely affect the optimization process.
Continuous variables are permitted as arguments to the GROUP= option. PROC HPMIXED does not sort by the values of the continuous variable; rather, it considers the data to be from a new group whenever the value of the continuous variable changes from the previous observation. Using a continuous variable decreases execution time for models with a large number of groups and also prevents the production of a large "Class Levels Information" table.
- NOFULLZ
-
eliminates the columns in
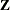 corresponding to missing levels of random effects involving CLASS variables. By default, these columns are included in
corresponding to missing levels of random effects involving CLASS variables. By default, these columns are included in 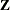 . It is sufficient to specify the NOFULLZ option in any RANDOM statement.
. It is sufficient to specify the NOFULLZ option in any RANDOM statement.
- SOLUTION
-
requests that the solution for the random-effects parameters be produced. Using notation from the section Model Assumptions, these estimates are the empirical best linear unbiased predictors (BLUPs)
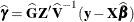 . They can be useful for comparing the random effects from different experimental units and can also be treated as residuals
in performing diagnostics for your mixed model.
. They can be useful for comparing the random effects from different experimental units and can also be treated as residuals
in performing diagnostics for your mixed model.
The numbers displayed in the SE Pred column of the "Solution for Random Effects" table are not the standard errors of the
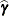 displayed in the Estimate column; rather, they are the standard errors of predictions
displayed in the Estimate column; rather, they are the standard errors of predictions 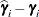 , where
, where 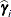 is the ith BLUP and
is the ith BLUP and 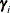 is the ith random-effect parameter.
is the ith random-effect parameter.
- SUBJECT=effect
-
identifies the subjects in your mixed model. Complete independence is assumed across subjects; thus, for the RANDOM statement, the SUBJECT= option produces a block-diagonal structure in
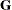 with identical blocks. The
with identical blocks. The 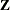 matrix is modified to accommodate this block-diagonality. In fact, specifying a subject effect is equivalent to nesting all
other effects in the RANDOM statement within the subject effect.
matrix is modified to accommodate this block-diagonality. In fact, specifying a subject effect is equivalent to nesting all
other effects in the RANDOM statement within the subject effect.
Continuous variables are permitted as arguments to the SUBJECT= option. PROC HPMIXED does not sort by the values of the continuous variable; rather, it considers the data to be from a new subject whenever the value of the continuous variable changes from the previous observation. Using a continuous variable decreases execution time for models with a large number of subjects and also prevents the production of a large "Class Levels Information" table.
- TYPE=covariance-structure
-
specifies the structure of the covariance matrix
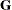 for random effects. The default structure is VC
.
for random effects. The default structure is VC
.
If you want different covariance structures in different parts of
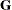 , you must use multiple RANDOM statements with different TYPE= options.
, you must use multiple RANDOM statements with different TYPE= options.
Valid values for covariance-structure are listed in Table 49.8. Examples are shown in Table 49.9.
Table 49.8: Covariance Structures
Structure
Description
Parameters
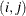 element
element
AR(1)
Autoregressive(1)
2
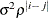
CHOL
Cholesky root
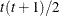
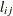
CS
Compound symmetry (CS)
2
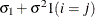
CSH
Heterogeneous CS
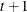
![$\sigma _ i\sigma _ j[\rho 1(i \neq j)+ 1(i=j)]$](images/statug_hpmixed0101.png)
UC
Uniform correlation (UC)
2
![$\sigma ^2[\rho 1(i \neq j) + 1(i=j)]$](images/statug_hpmixed0102.png)
UCH
Heterogeneous UC
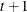
![$\sigma _ i\sigma _ j[\rho 1(i \neq j) + 1(i=j)]$](images/statug_hpmixed0103.png)
UN
Unstructured
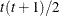
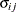
VC
Variance components
q
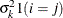
and i,j correspond to kth effect
In Table 49.8, t is the overall dimension of the covariance matrix, and
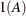 equals 1 when A is true and 0 otherwise. For example, 1(i = j) equals 1 when i = j and equals 0 otherwise. TYPE=UCH is the same as TYPE=CSH.
equals 1 when A is true and 0 otherwise. For example, 1(i = j) equals 1 when i = j and equals 0 otherwise. TYPE=UCH is the same as TYPE=CSH.
Table 49.9 lists some examples of the structures in Table 49.8.
Table 49.9: Covariance Structure Examples
Description
Structure
Example
First-order
autoregressiveAR(1)
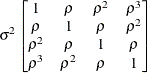
Cholesky
rootCHOL
![$ \left[\begin{array}{llll} l_{11} & 0 & 0 & 0 \\ l_{21} & l_{22} & 0 & 0 \\ l_{31} & l_{32} & l_{33} & 0 \\ l_{41} & l_{42} & l_{43} & l_{44} \end{array}\right] \left[\begin{array}{llll} l_{11} & l_{21} & l_{31} & l_{41} \\ 0 & l_{22} & l_{32} & l_{42} \\ 0 & 0 & l_{33} & l_{43} \\ 0 & 0 & 0 & l_{44} \end{array} \right] $](images/statug_hpmixed0108.png)
Compound
symmetryCS
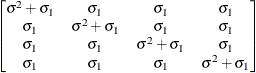
Uniform
correlationUC
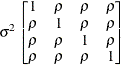
Heterogeneous
UCUCH
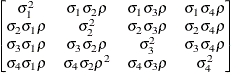
Unstructured
UN
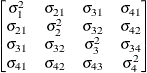
Variance
componentsVC (default)
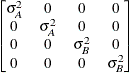
The variances and covariances in the formulas that follow in the TYPE= descriptions are expressed in terms of generic random variables
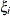 and
and 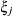 . They represent random effects for which the
. They represent random effects for which the 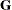 matrices are constructed.
matrices are constructed.
The following list provides some further information about these covariance-structures:
- AR(1)
-
specifies a first-order autoregressive structure,
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \sigma ^2 \rho ^{|i - j|} \]](images/statug_hpmixed0116.png)
The values i and j are derived for the ith and jth observations, respectively. For example, in the following statements the values correspond to the class levels for the
timeeffect of the ith and jth observation within a particular subject:proc hpmixed; class time patient; model y = x x*x; random time / sub=patient type=ar(1); run;
PROC HPMIXED imposes the constraint
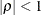 for stationarity.
for stationarity.
- CHOL
-
specifies an unstructured variance-covariance matrix parameterized through its Cholesky root. All diagonal values are constrained to be positive. This parameterization guarantees a positive definite covariance matrix. For example, a
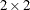 unstructured covariance matrix can be written as
unstructured covariance matrix can be written as
![\[ \mr{Var}[\bxi ] = \left[ \begin{array}{cc} \sigma ^2_1 & \sigma _{21} \\ \sigma _{21} & \sigma ^2_2 \end{array} \right] \]](images/statug_hpmixed0119.png)
Without imposing constraints on the three parameters, there is no guarantee that the estimated variance matrix is positive definite. Even if
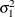 and
and 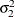 are nonzero, a large value for
are nonzero, a large value for 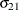 can lead to a negative eigenvalue of
can lead to a negative eigenvalue of ![$\mr{Var}[\bxi ]$](images/statug_hpmixed0123.png) . The Cholesky root of a positive definite matrix
. The Cholesky root of a positive definite matrix  is a lower triangular matrix
is a lower triangular matrix  such that
such that 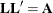 . The Cholesky root of the above
. The Cholesky root of the above 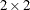 matrix can be written as
matrix can be written as
![\[ \mb{L} = \left[ \begin{array}{cc} l_{11} & 0 \\ l_{21} & l_{22} \end{array} \right] \]](images/statug_hpmixed0126.png)
The elements of the unstructured variance matrix are then simply
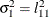 ,
, 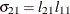 , and
, and 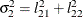 . Similar operations yield the generalization to covariance matrices of higher orders.
. Similar operations yield the generalization to covariance matrices of higher orders.
For example, the following statements model the covariance matrix of each subject as an unstructured matrix:
proc hpmixed; class sub; model y = x; random time / sub=patient type=chol; run;
The HPMIXED procedure constrains the diagonal elements of the Cholesky root to be positive. This guarantees that the structure is positive definite.
- CS
-
specifies the compound-symmetry structure, which has constant variance and constant covariance
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \left\{ \begin{array}{lc} \sigma ^2 + \sigma _1 & i=j \\ \sigma _1 & i \not= j \end{array} \right. \]](images/statug_hpmixed0130.png)
Under compound-symmetry, the
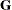 matrix is of form
matrix is of form 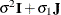 . The variance parameter
. The variance parameter 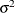 is constrained to be positive, and the covariance parameter
is constrained to be positive, and the covariance parameter 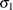 is constrained to be greater than
is constrained to be greater than 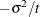 where t is the dimension of the structure. This guarantees the structure is positive definite. The compound-symmetry structure arises
naturally with nested random effects, such as when a subsampling error is nested within an experimental error.
where t is the dimension of the structure. This guarantees the structure is positive definite. The compound-symmetry structure arises
naturally with nested random effects, such as when a subsampling error is nested within an experimental error.
- CSH
-
specifies the heterogeneous compound-symmetry structure. This structure has a different variance parameter for each diagonal element, and it uses the square roots of these parameters in the off-diagonal entries. In Table 49.8,
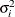 is the ith variance parameter that satisfies
is the ith variance parameter that satisfies 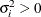 , and
, and 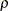 is the correlation parameter that satisfies
is the correlation parameter that satisfies 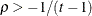 , where t is the dimension of the structure. This guarantees that the structure is positive definite.
, where t is the dimension of the structure. This guarantees that the structure is positive definite.
- UC
-
specifies the uniform correlation structure, which has constant variance and constant correlation
![\[ \mr{Cov}\left[\xi _ i,\xi _ j\right] = \left\{ \begin{array}{lc} \sigma ^2 & i=j \\ \sigma ^2\rho & i \not= j \end{array} \right. \]](images/statug_hpmixed0139.png)
Under uniform correlation, the
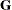 matrix is of form
matrix is of form ![$\sigma ^2[(1-\rho )\bI + \rho \bJ ]$](images/statug_hpmixed0140.png) . The variance
. The variance 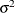 is constrained to be positive, and the correlation
is constrained to be positive, and the correlation 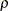 is constrained to be greater than
is constrained to be greater than 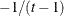 , where t is the dimension of the structure. This guarantees the structure is positive definite. This structure is equivalent to the
compound-symmetry structure with a better numerical property in terms of optimization.
, where t is the dimension of the structure. This guarantees the structure is positive definite. This structure is equivalent to the
compound-symmetry structure with a better numerical property in terms of optimization.
The uniform correlation structure arises frequently in agriculture and animal sciences.
- UCH
-
specifies the heterogeneous uniform correlation structure. This structure has a different variance parameter for each diagonal element, and it uses the square roots of these parameters in the off-diagonal entries. In Table 49.8,
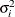 is the ith variance parameter that satisfies
is the ith variance parameter that satisfies 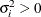 , and
, and 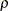 is the correlation parameter that satisfies
is the correlation parameter that satisfies 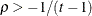 , where t is the dimension of the structure. This guarantees that the structure is positive definite.
, where t is the dimension of the structure. This guarantees that the structure is positive definite.
- UN
-
specifies a completely general (unstructured) covariance matrix parameterized directly in terms of variances and covariances. The variances are constrained to be positive, and the covariances are unconstrained. In addition, this structure is internally constrained to be positive definite.
- VC
-
specifies standard variance components and is the default structure for the RANDOM and REPEATED statements. In the RANDOM statement, a distinct variance component is assigned to each effect. In the REPEATED statement, this structure is usually used only with the GROUP= option to specify a heterogeneous variance model.
