The GLMPOWER Procedure
If you specify covariates in a univariate model (whether continuous or categorical), then two adjustments are made in order
to compute approximate power in the presence of the covariates. Let ![]() denote the number of covariates (counting dummy variables for categorical covariates individually) as specified in the NCOVARIATES=
option in the POWER
statement. In other words,
denote the number of covariates (counting dummy variables for categorical covariates individually) as specified in the NCOVARIATES=
option in the POWER
statement. In other words, ![]() is the total degrees of freedom used by the covariates. The adjustments are as follows:
is the total degrees of freedom used by the covariates. The adjustments are as follows:
-
The error degrees of freedom decrease by
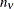 .
.
-
The error standard deviation
 shrinks by a factor of
shrinks by a factor of 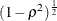 (if the CORRXY=
option is used to specify the correlation
(if the CORRXY=
option is used to specify the correlation 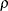 between covariates and response) or
between covariates and response) or 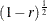 (if the PROPVARREDUCTION=
option is used to specify the proportional reduction in total
(if the PROPVARREDUCTION=
option is used to specify the proportional reduction in total 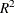 incurred by the covariates). Let
incurred by the covariates). Let 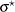 represent the updated value of
represent the updated value of  .
.
As a result of these changes, the power is computed as
where ![]() is calculated using
is calculated using ![]() rather than
rather than ![]() :
:
