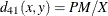The DISTANCE Procedure
The following notation is used in this section:
- v
-
the number of variables or the dimensionality
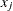
-
data for observation x and the jth variable, where
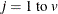
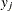
-
data for observation y and the jth variable, where
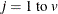
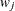
-
weight for the jth variable from the WEIGHTS= option in the VAR statement.
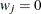 when either
when either 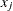 or
or 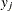 is missing.
is missing.
- W
-
the sum of total weights. No matter if the observation is missing or not, its weight is added to this metric.

-
mean for observation x
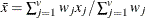
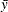
-
mean for observation y
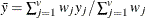
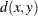
-
the distance or dissimilarity between observations x and y
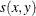
-
the similarity between observations x and y
The factor ![]() is used to adjust some of the proximity measures for missing values.
is used to adjust some of the proximity measures for missing values.
- EUCLID
- SQEUCLID
- SIZE
- SHAPE
-
Note: squared shape distance plus squared size distance equals squared Euclidean distance.
- COV
-
covariance similarity coefficient
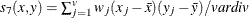 , where
, where
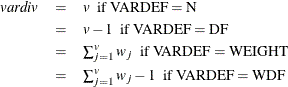
- CORR
- DCORR
-
correlation transformed to Euclidean distance as sqrt(1–CORR)
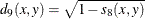
- SQCORR
- DSQCORR
-
squared correlation transformed to squared Euclidean distance as (1–SQCORR)
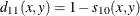
- L(p)
-
Minkowski (
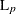 ) distance, where p is a positive numeric value
) distance, where p is a positive numeric value ![$ d_{12}(x,y) = [ (\sum _{j=1}^ v{w_ j{|x_ j-y_ j|}^ p}) W / (\sum _{j=1}^{v}w_ j) ]^{1/p} $](images/statug_distance0064.png)
- CITYBLOCK
- CHEBYCHEV
- POWER(p,r)
-
generalized Euclidean distance, where p is a nonnegative numeric value and r is a positive numeric value. The distance between two observations is the rth root of sum of the absolute differences to the pth power between the values for the observations:
![$ d_{15}(x,y) = [ (\sum _{j=1}^ v{w_ j{|x_ j-y_ j| }^ p}) W / (\sum _{j=1}^{v}w_ j) ]^{1/r} $](images/statug_distance0067.png)
- SIMRATIO
- DISRATIO
- NONMETRIC
- CANBERRA
-
Canberra metric coefficient. See Sneath and Sokal (1973, pp. 125–126)
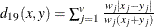
- COSINE
- DOT
- OVERLAP
- DOVERLAP
- CHISQ
-
chi-square If the data represent the frequency counts, chi-square dissimilarity between two sets of frequencies can be computed. A 2-by-v contingency table is illustrated to explain how the chi-square dissimilarity is computed as follows:
Variable
Row
Observation
Var 1
Var 2
…
Var v
Sum
X
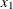
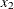
…
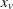
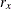
Y
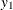
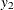
…
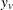
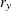
Column Sum
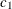
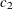
…
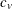
T
where
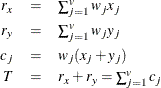
The chi-square measure is computed as follows:
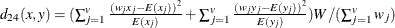
where for j= 1, 2, …, v
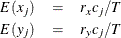
- CHI
- PHISQ
-
phi-square This is the CHISQ dissimilarity normalized by the sum of weights
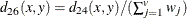
- PHI
The following notation is used for computing ![]() to
to ![]() . Notice that only the nonmissing pairs are discussed below; all the pairs with at least one missing value will be excluded
from any of the computations in the following section because
. Notice that only the nonmissing pairs are discussed below; all the pairs with at least one missing value will be excluded
from any of the computations in the following section because ![]()
- M
-
nonmissing matches
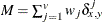 , where
, where
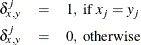
- X
-
nonmissing mismatches
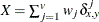 , where
, where
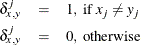
- N
-
total nonmissing pairs
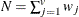
- HAMMING
- MATCH
- DMATCH
-
simple matching coefficient transformed to Euclidean distance
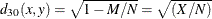
- DSQMATCH
-
simple matching coefficient transformed to squared Euclidean distance
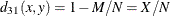
- HAMANN
- RT
- SS1
- SS3
-
Sokal and Sneath 3. The coefficient between an observation and itself is always indeterminate (missing) since there is no mismatch.
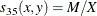
The following notation is used for computing ![]() to
to ![]() . Notice that only the nonmissing pairs are discussed in the following section; all the pairs with at least one missing value
are excluded from any of the computations in the following section because
. Notice that only the nonmissing pairs are discussed in the following section; all the pairs with at least one missing value
are excluded from any of the computations in the following section because ![]()
Also, the observed nonmissing data of an asymmetric binary variable can have only two possible outcomes: presence or absence. Therefore, the notation, PX (present mismatches), always has a value of zero for an asymmetric binary variable.
The following methods distinguish between the presence and absence of attributes.
- X
-
mismatches with at least one present
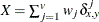 , where
, where

- PM
-
present matches
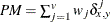 , where
, where
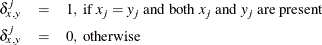
- PX
-
present mismatches
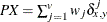 , where
, where
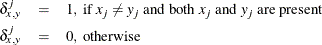
- PP
-
both present = PM + PX
- P
-
at least one present = PM + X
- PAX
-
present-absent mismatches
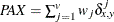 , where
, where
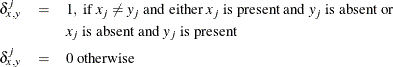
- N
-
total nonmissing pairs
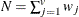
- JACCARD
-
Jaccard similarity coefficient
The JACCARD method is equivalent to the SIMRATIO method if there are only ratio variables; if there are both ratio and asymmetric nominal variables, the coefficient is computed as sum of the coefficient from the ratio variables (SIMRATIO) and the coefficient from the asymmetric nominal variables.
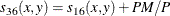
- DJACCARD
-
Jaccard dissimilarity coefficient
The DJACCARD method is equivalent to the DISRATIO method if there are only ratio variables; if there are both ratio and asymmetric nominal variables, the coefficient is computed as sum of the coefficient from the ratio variables (DISRATIO) and the coefficient from the asymmetric nominal variables.
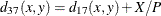
- DICE
-
Dice coefficient or Czekanowski/Sorensen similarity coefficient
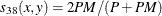
- RR
-
Russell and Rao. This is the binary equivalent of the dot product coefficient.
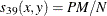
- BLWNM | BRAYCURTIS
-
Binary Lance and Williams, also known as Bray and Curtis coefficient
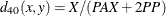
- K1
-
Kulcynski 1. The coefficient between an observation and itself is always indeterminate (missing) since there is no mismatch.