The SEQDESIGN Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics
Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics -
Examples
 Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual
Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual - References
For each design, the SEQDESIGN procedure displays the “Design Information,” “Method Information,” and “Boundary Information” tables by default.
The “Boundary Information” table displays the following information at each stage:
-
proportion of information
-
actual information level, if the maximum information is either specified or derived
-
alternative references with the specified statistic scale. If a p-value scale is specified, the standardized Z scale is used.
-
boundary values with the specified statistic scale to reject or accept the null hypothesis
Note that implicitly, the boundary information table also contains variables for the boundary scale, stopping criterion, and
type of alternative hypothesis. That is, if an ODS statement is used to save the table, the data set also contains the variables
_Scale_ for the boundary scale, _Stop_ for the stopping criterion, and _ALT_ for the type of alternative hypothesis.
The “Design Information” table displays the design specifications and derived statistics. The derived Max Information (Percent Fixed-Sample) is the maximum information for the sequential design in percentage of the corresponding fixed-sample information.
The Null Ref ASN (Percent Fixed-Sample) is the average sample number (expected sample size for nonsurvival data or expected number of events for survival data) required under the null hypothesis for the group sequential design in percentage of the corresponding fixed-sample design. Similarly, the Alt Ref ASN (Percent Fixed-Sample) is the average sample number required under the alternative reference for the group sequential design in percentage of the corresponding fixed-sample design.
If both the maximum information (MAXINFO= option) and the alternative reference ![]() (ALTREF= option) are specified, then either the ALPHA= option is used to derive the Type II error probability
(ALTREF= option) are specified, then either the ALPHA= option is used to derive the Type II error probability ![]() (BOUNDARYKEY=ALPHA) or the BETA= option is used to derive the Type I error probability
(BOUNDARYKEY=ALPHA) or the BETA= option is used to derive the Type I error probability ![]() (BOUNDARYKEY=BETA).
(BOUNDARYKEY=BETA).
The “Error Spending Information” table displays the following information at each stage:
-
proportion of information
-
actual information level, if the maximum information is either specified or derived
-
cumulative error spending for each boundary
The “Method Information” table displays detailed method information for the design. For each boundary, it displays the following:
-
the group sequential method used
-
the
 or
or 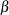 errors
errors
-
the specified parameter
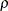 , if an error spending function is used
, if an error spending function is used
-
the specified parameters
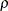 and
and  with the derived critical value C, if a unified family method is used
with the derived critical value C, if a unified family method is used
-
the alternative reference
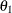 , if either the ALTREF= or the MAXINFO= option is specified
, if either the ALTREF= or the MAXINFO= option is specified
-
the derived drift parameter,
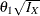 , where
, where 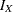 is the maximum information and
is the maximum information and 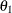 is the alternative reference
is the alternative reference
Note that the alternative references are displayed with the MLE scale in the “Method Information” table. In contrast, the alternative references in the “Boundary Information” table are displayed with the specified statistic scale (if the p-value scale is not specified) or the standardized Z scale (if the p-value scale is specified).
The “Powers and Expected Sample Sizes” table displays the following information under each of the specified hypothetical references ![]() , where
, where ![]() is the alternative reference and
is the alternative reference and ![]() are values specified in the CREF= option.
are values specified in the CREF= option.
-
coefficient
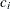 for the hypothetical references. The value
for the hypothetical references. The value 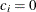 corresponds to the null hypothesis and
corresponds to the null hypothesis and 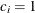 corresponds to the alternative hypothesis
corresponds to the alternative hypothesis
-
power
-
expected sample size, as percentage of fixed-sample size
For a one-sided design, the power and expected sample sizes under the hypothetical references ![]() are displayed.
are displayed.
For a two-sided symmetric design, the power and expected sample sizes under each of the hypothetical references ![]() are displayed, where
are displayed, where ![]() is the upper alternative reference.
is the upper alternative reference.
For a two-sided asymmetric design,
the power and expected sample sizes under each of the hypothetical references ![]() and
and ![]() are displayed, where
are displayed, where ![]() and
and ![]() are the lower and upper alternative references, respectively.
are the lower and upper alternative references, respectively.
For a two-sided design, the power is the probability of correctly rejecting the null hypothesis for the correct alternative.
Thus, under the null hypothesis, the displayed power corresponds to a one-sided Type I error probability level—that is, the
lower ![]() level or the upper
level or the upper ![]() level.
level.
The expected sample size as a percentage of the corresponding fixed-sample design is
where ![]() is the stopping probability at stage k,
is the stopping probability at stage k, ![]() is the expected information level, and
is the expected information level, and ![]() is the information level for the fixed-sample design.
is the information level for the fixed-sample design.
When you use the SAMPLESIZE statement with the SEQDESIGN procedure, the “Sample Size Summary” table displays parameters for the sample size computation. It also displays the expected sample sizes or numbers of events for the model under both the null and alternative hypotheses.
The expected sample size is the average sample size
where ![]() is the stopping probability at stage k,
is the stopping probability at stage k, ![]() is the expected information level,
is the expected information level, ![]() is the information level for the fixed-sample design, and
is the information level for the fixed-sample design, and ![]() is the sample size for the fixed-sample design.
is the sample size for the fixed-sample design.
The expected number of events is the average number of events
where ![]() is the fixed-sample number of events for the model.
is the fixed-sample number of events for the model.
The “Sample Sizes (N)” table displays the required sample sizes and information levels at each stage, in both fractional and integer numbers. The derived fractional sample sizes are under the heading “Fractional N.” These sample sizes are rounded up to integers under the heading “Ceiling N.” The matched integer sample sizes are also displayed for two-sample tests.
The “Required Number of Events (D)” table displays the required number of events required and information level at each stage.
The “Number of Events (D) and Sample Sizes (N)” table displays the number of events and sample size required at each stage with the study time. The derived times under the heading “Fractional Time” are not integers. These times are rounded up to integers under the heading “Ceiling Time.”
The “Expected Cumulative Stopping Probabilities” table displays the following information under each of the specified hypothetical references ![]() , where
, where ![]() are values specified in the CREF= option, and
are values specified in the CREF= option, and ![]() is the alternative reference:
is the alternative reference:
-
coefficient
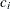 for the hypothetical references. The value
for the hypothetical references. The value 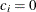 corresponds to the null hypothesis, and
corresponds to the null hypothesis, and 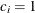 corresponds to the alternative hypothesis
corresponds to the alternative hypothesis
-
expected stopping stage
-
source of the stopping probability: reject
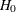 (with STOP=REJECT or STOP=BOTH), accept
(with STOP=REJECT or STOP=BOTH), accept 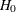 (with STOP=ACCEPT or STOP=BOTH), or either reject or accept
(with STOP=ACCEPT or STOP=BOTH), or either reject or accept 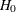 (with STOP=BOTH)
(with STOP=BOTH)
-
expected cumulative stopping probabilities at each stage
For a one-sided design, the expected cumulative stopping probabilities under the hypothetical references ![]() are displayed.
are displayed.
For a two-sided design, the expected cumulative stopping probabilities under each of the hypothetical references ![]() and
and ![]() are displayed, where
are displayed, where ![]() and
and ![]() are the lower and upper alternative references, respectively.
are the lower and upper alternative references, respectively.
Note that for a symmetric two-sided design, only the expected cumulative stopping probabilities under the hypothetical references
![]() are derived.
are derived.
The expected stopping stage is given by ![]() , where the integer
, where the integer ![]() and the fraction d (
and the fraction d (![]() ) are derived from the expected information level equation
) are derived from the expected information level equation
where ![]() is the stopping probability at stage k.
is the stopping probability at stage k.
For equally spaced information levels, the expected stopping stage is reduced to the weighted average