The SEQDESIGN Procedure
-
Overview

- Getting Started
-
Syntax

-
Details
 Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics
Fixed-Sample Clinical TrialsOne-Sided Fixed-Sample Tests in Clinical TrialsTwo-Sided Fixed-Sample Tests in Clinical TrialsGroup Sequential MethodsStatistical Assumptions for Group Sequential DesignsBoundary ScalesBoundary VariablesType I and Type II ErrorsUnified Family MethodsHaybittle-Peto MethodWhitehead MethodsError Spending MethodsAcceptance (beta) BoundaryBoundary Adjustments for Overlapping Lower and Upper beta BoundariesSpecified and Derived ParametersApplicable Boundary KeysSample Size ComputationApplicable One-Sample Tests and Sample Size ComputationApplicable Two-Sample Tests and Sample Size ComputationApplicable Regression Parameter Tests and Sample Size ComputationAspects of Group Sequential DesignsSummary of Methods in Group Sequential DesignsTable OutputODS Table NamesGraphics OutputODS Graphics -
Examples
 Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual
Creating Fixed-Sample DesignsCreating a One-Sided O’Brien-Fleming DesignCreating Two-Sided Pocock and O’Brien-Fleming DesignsGenerating Graphics Display for Sequential DesignsCreating Designs Using Haybittle-Peto MethodsCreating Designs with Various Stopping CriteriaCreating Whitehead’s Triangular DesignsCreating a One-Sided Error Spending DesignCreating Designs with Various Number of StagesCreating Two-Sided Error Spending Designs with and without Overlapping Lower and Upper beta BoundariesCreating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject H0Creating a Two-Sided Asymmetric Error Spending Design with Early Stopping to Reject or Accept H0Creating a Design with a Nonbinding Beta BoundaryComputing Sample Size for Survival Data That Have Uniform AccrualComputing Sample Size for Survival Data with Truncated Exponential Accrual - References
The SEQDESIGN procedure assumes that with a total number of stages K, the sequence of the standardized test statistics ![]() has the canonical joint distribution with information levels
has the canonical joint distribution with information levels ![]() for the parameter
for the parameter ![]() (Jennison and Turnbull, 2000, p. 49):
(Jennison and Turnbull, 2000, p. 49):
-
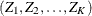 is multivariate normal
is multivariate normal
-
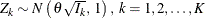
-
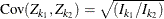 ,
, 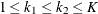
In terms of the maximum likelihood estimator, ![]() ,
, ![]() , the canonical joint distribution can be expressed as follows:
, the canonical joint distribution can be expressed as follows:
-
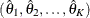 is multivariate normal
is multivariate normal
-
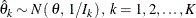
-
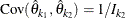 ,
, 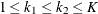
Furthermore, in terms of the score statistics ![]() ,
, ![]() , the canonical joint distribution can be expressed as follows:
, the canonical joint distribution can be expressed as follows:
-
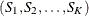 is multivariate normal
is multivariate normal
-
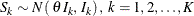
-
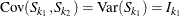 ,
, 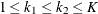
That is, the increments ![]() ,
, ![]() , …, and
, …, and ![]() are independently distributed.
are independently distributed.
If the test statistic is computed from the data that are not from a normal distribution, such as a binomial distribution, then it is assumed that the test statistic is computed from a large sample such that the statistic has an approximately normal distribution.
If the increments ![]() ,
, ![]() , …, and
, …, and ![]() are not independently distributed, then it is inappropriate to use group sequential methods in the SEQDESIGN procedure. One
such example is the Gehan statistic, which is a weighted log-rank statistic for censored data. See Jennison and Turnbull (2000, pp. 232–233, 276–277) and Proschan, Lan, and Wittes (2006, pp. 150–151) for a description of statistics with nonindependent increments.
are not independently distributed, then it is inappropriate to use group sequential methods in the SEQDESIGN procedure. One
such example is the Gehan statistic, which is a weighted log-rank statistic for censored data. See Jennison and Turnbull (2000, pp. 232–233, 276–277) and Proschan, Lan, and Wittes (2006, pp. 150–151) for a description of statistics with nonindependent increments.
If a trial stops at an early interim stage with only a small number of responses observed, it can lead to a distrust of the statistical findings, which rely on the assumption that the sample is large (Whitehead, 1997, p. 167). A group sequential design can be specified such that at the first interim analysis, there are a sufficient number of responses to ensure that the analysis to be conducted is both reliable and persuasive (Whitehead, 1997, p. 167).
Alternatively, a method such as the O’Brien-Fleming method can be used to derive conservative stopping boundary values at very early stages to make the early stop less likely. That is, the trial is stopped in early stages only with overwhelming evidence.
A simple example of the group sequential tests is the test for a normal mean, ![]() . Suppose
. Suppose ![]() are n observations of a response variable
are n observations of a response variable Y in a data set from a normal distribution with an unknown mean ![]() and a known variance
and a known variance ![]() . Then the maximum likelihood estimate of
. Then the maximum likelihood estimate of ![]() is the sample mean
is the sample mean
The sample mean has a normal distribution with mean ![]() and variance
and variance ![]() :
:
An equivalent hypothesis for ![]() is
is ![]() , where
, where ![]() . The MLE statistic for
. The MLE statistic for ![]() ,
,
where the information ![]() .
.
For a group sequential test with K stages, there are ![]() observations available at these stages. At stage k, the sample mean is computed as
observations available at these stages. At stage k, the sample mean is computed as
where ![]() is the value of the jth observation available at the kth stage and
is the value of the jth observation available at the kth stage and ![]() is the cumulative sample size at stage k, which includes the
is the cumulative sample size at stage k, which includes the ![]() observations collected at previous stages and the
observations collected at previous stages and the ![]() observations collected at the current stage.
observations collected at the current stage.
The maximum likelihood estimate
where the information
is the inverse of the variance.
Thus, the standardized statistic
The covariance of ![]() and
and ![]() ,
, ![]() can be expressed as
can be expressed as
where ![]() and
and ![]() .
.
Since ![]() is independent of
is independent of ![]() ,
, ![]() and
and
Thus the statistics ![]() has the canonical joint distribution with information levels
has the canonical joint distribution with information levels ![]() for the parameter
for the parameter ![]() . See the section Applicable One-Sample Tests and Sample Size Computation, the section Applicable Two-Sample Tests and Sample Size Computation, and the section Applicable Regression Parameter Tests and Sample Size Computation for more examples of applicable tests in group sequential trials.
. See the section Applicable One-Sample Tests and Sample Size Computation, the section Applicable Two-Sample Tests and Sample Size Computation, and the section Applicable Regression Parameter Tests and Sample Size Computation for more examples of applicable tests in group sequential trials.