The PROBIT Procedure
- Overview
-
Getting Started

-
Syntax
 PROC PROBIT StatementBY StatementCDFPLOT StatementCLASS StatementEFFECTPLOT StatementESTIMATE StatementINSET StatementIPPPLOT StatementLPREDPLOT StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementPREDPPLOT StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement
PROC PROBIT StatementBY StatementCDFPLOT StatementCLASS StatementEFFECTPLOT StatementESTIMATE StatementINSET StatementIPPPLOT StatementLPREDPLOT StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementPREDPPLOT StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement -
Details
 Missing ValuesResponse Level OrderingComputational MethodDistributionsINEST= SAS-data-setModel SpecificationLack-of-Fit TestsRescaling the Covariance MatrixTolerance DistributionInverse Confidence LimitsOUTEST= SAS-data-setXDATA= SAS-data-setTraditional High-Resolution GraphicsDisplayed OutputODS Table NamesODS Graphics
Missing ValuesResponse Level OrderingComputational MethodDistributionsINEST= SAS-data-setModel SpecificationLack-of-Fit TestsRescaling the Covariance MatrixTolerance DistributionInverse Confidence LimitsOUTEST= SAS-data-setXDATA= SAS-data-setTraditional High-Resolution GraphicsDisplayed OutputODS Table NamesODS Graphics -
Examples

- References
In this example, two preparations, a standard preparation and a test preparation, are each given at several dose levels to groups of insects. The symptoms are recorded for each insect within each group, and two multilevel probit models are fit. Because the natural sort order of the three levels is not the same as the response order, the ORDER=DATA option is specified in the PROC PROBIT statement to get the desired order. The following statements fit two models:
data multi; input Prep $ Dose Symptoms $ N; LDose=log10(Dose); if Prep='test' then PrepDose=LDose; else PrepDose=0; datalines; stand 10 None 33 stand 10 Mild 7 stand 10 Severe 10 stand 20 None 17 stand 20 Mild 13 stand 20 Severe 17 stand 30 None 14 stand 30 Mild 3 stand 30 Severe 28 stand 40 None 9 stand 40 Mild 8 stand 40 Severe 32 test 10 None 44 test 10 Mild 6 test 10 Severe 0 test 20 None 32 test 20 Mild 10 test 20 Severe 12 test 30 None 23 test 30 Mild 7 test 30 Severe 21 test 40 None 16 test 40 Mild 6 test 40 Severe 19 ;
proc probit order=data data=multi; class Prep Symptoms; nonpara: model Symptoms=Prep LDose PrepDose / lackfit; weight N; run;
proc probit order=data data=multi; class Prep Symptoms; parallel: model Symptoms=Prep LDose / lackfit; weight N; run;
Results of these two models are shown in Output 79.2.1 and Output 79.2.2. The first model allows for nonparallelism between the dose response curves for the two preparations by inclusion of an interaction
between Prep and LDose. The interaction term is labeled PrepDose in the “Analysis of Parameter Estimates” table. The results of this first model indicate that the parameter for the interaction term is not significant, having a
Wald chi-square of 0.73. Also, since the first model is a generalization of the second, a likelihood ratio test statistic
for this same parameter can be obtained by multiplying the difference in log likelihoods between the two models by 2. The
value obtained, ![]() , is 0.73. This is in close agreement with the Wald chi-square from the first model. The lack-of-fit test statistics for the
two models do not indicate a problem with either fit.
, is 0.73. This is in close agreement with the Wald chi-square from the first model. The lack-of-fit test statistics for the
two models do not indicate a problem with either fit.
Output 79.2.1: Multilevel Response: Nonparallel Analysis
| Model Information | |
|---|---|
| Data Set | WORK.MULTI |
| Dependent Variable | Symptoms |
| Weight Variable | N |
| Number of Observations | 23 |
| Name of Distribution | Normal |
| Log Likelihood | -345.9401767 |
| Class Level Information | ||
|---|---|---|
| Name | Levels | Values |
| Prep | 2 | stand test |
| Symptoms | 3 | None Mild Severe |
| Analysis of Maximum Likelihood Parameter Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | 95% Confidence Limits | Chi-Square | Pr > ChiSq | ||
| Intercept | 1 | 3.8080 | 0.6252 | 2.5827 | 5.0333 | 37.10 | <.0001 | |
| Intercept2 | 1 | 0.4684 | 0.0559 | 0.3589 | 0.5780 | 70.19 | <.0001 | |
| Prep | stand | 1 | -1.2573 | 0.8190 | -2.8624 | 0.3479 | 2.36 | 0.1247 |
| Prep | test | 0 | 0.0000 | . | . | . | . | . |
| LDose | 1 | -2.1512 | 0.3909 | -2.9173 | -1.3851 | 30.29 | <.0001 | |
| PrepDose | 1 | -0.5072 | 0.5945 | -1.6724 | 0.6580 | 0.73 | 0.3935 | |
Output 79.2.2: Multilevel Response: Parallel Analysis
| Model Information | |
|---|---|
| Data Set | WORK.MULTI |
| Dependent Variable | Symptoms |
| Weight Variable | N |
| Number of Observations | 23 |
| Name of Distribution | Normal |
| Log Likelihood | -346.306141 |
| Class Level Information | ||
|---|---|---|
| Name | Levels | Values |
| Prep | 2 | stand test |
| Symptoms | 3 | None Mild Severe |
| Analysis of Maximum Likelihood Parameter Estimates | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Estimate | Standard Error | 95% Confidence Limits | Chi-Square | Pr > ChiSq | ||
| Intercept | 1 | 3.4148 | 0.4126 | 2.6061 | 4.2235 | 68.50 | <.0001 | |
| Intercept2 | 1 | 0.4678 | 0.0558 | 0.3584 | 0.5772 | 70.19 | <.0001 | |
| Prep | stand | 1 | -0.5675 | 0.1259 | -0.8142 | -0.3208 | 20.33 | <.0001 |
| Prep | test | 0 | 0.0000 | . | . | . | . | . |
| LDose | 1 | -2.3721 | 0.2949 | -2.9502 | -1.7940 | 64.68 | <.0001 | |
The negative coefficient associated with LDose indicates that the probability of having no symptoms (Symptoms=’None’) or no or mild symptoms (Symptoms=’None’ or Symptoms=’Mild’) decreases as LDose increases; that is, the probability of a severe symptom increases with LDose. This association is apparent for both treatment groups.
The negative coefficient associated with the standard treatment group (Prep = stand) indicates that the standard treatment is associated with more severe symptoms across all Ldose values.
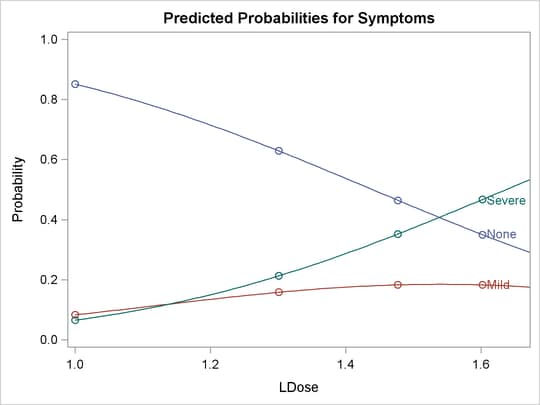
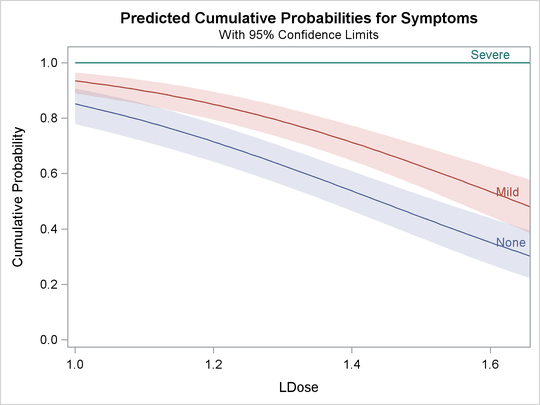
The following statements use the PLOTS= option to create the plot shown in Output 79.2.3 and Output 79.2.4. Output 79.2.3 is the plot of the probabilities of the response taking on individual levels as a function of LDose. Since there are two covariates, LDose and Prep, the value of the classification variable Prep is fixed at the highest level, test. Instead of individual response level probabilities, the CDFPLOT option creates the plot of the cumulative response probabilities
with confidence limits shown in Output 79.2.4.
proc probit data=multi order=data
plots=(predpplot(level=("None" "Mild" "Severe"))
cdfplot(level=("None" "Mild" "Severe")));
class Prep Symptoms;
parallel: model Symptoms=Prep LDose / lackfit;
weight N;
run;
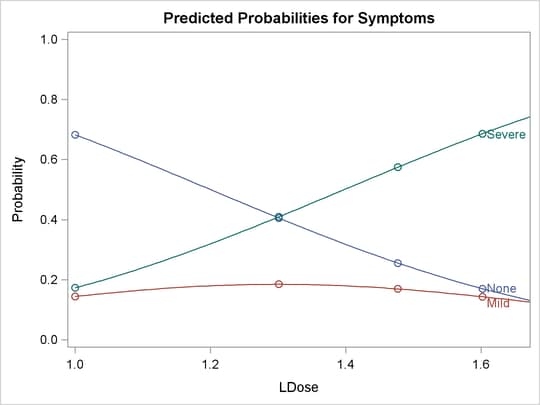
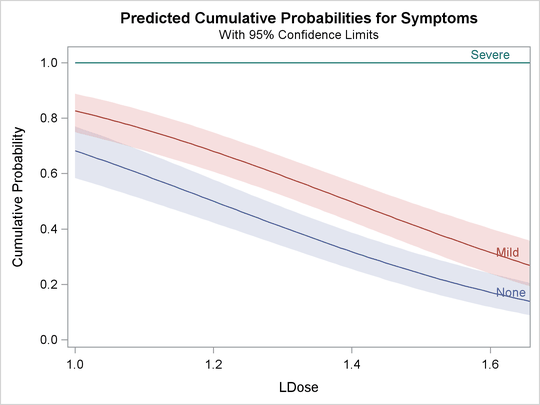
The following statements use the XDATA= data set to create plots of predicted probabilities and cumulative probabilities with
Prep set to the stand level. The resulting plots are shown in Output 79.2.5 and Output 79.2.6.
data xrow;
input Prep $ Dose Symptoms $ N;
LDose=log10(Dose);
datalines;
stand 40 Severe 32
run;
proc probit data=multi order=data xdata=xrow
plots=(predpplot(level=("None" "Mild" "Severe"))
cdfplot(level=("None" "Mild" "Severe")));
class Prep Symptoms;
parallel: model Symptoms=Prep LDose / lackfit;
weight N;
run;