The PHREG Procedure
- Overview
-
Getting Started

-
Syntax
 PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement
PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement -
Details
 Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelProportional Rates/Means Models for Recurrent EventsThe Frailty ModelProportional Subdistribution Hazards Model for Competing-Risks DataHazard RatiosNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsSchemper-Henderson Predictive MeasureResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics
Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelProportional Rates/Means Models for Recurrent EventsThe Frailty ModelProportional Subdistribution Hazards Model for Competing-Risks DataHazard RatiosNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsSchemper-Henderson Predictive MeasureResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential ModelAnalysis of Competing-Risks Data
Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential ModelAnalysis of Competing-Risks Data - References
When experimental units are naturally or artificially clustered, failure times of experimental units within a cluster are correlated. Two approaches can be taken to adjust for the intracluster correlation. In the marginal Cox model approach, Lee, Wei, and Amato (1992) estimate the regression parameters in the Cox model by the maximum partial likelihood estimates under an independent working assumption and use a robust sandwich covariance matrix estimate to account for the intracluster dependence. Lin (1994) illustrates this methodology by using a subset of data from the Diabetic Retinopathy Study (DRS). An alternative approach to account for the within-cluster correlation is to use a shared frailty model where cluster effects are incorporated into the model as independent and identically distributed random variables.
The following DATA step creates the data set Blind that represents 197 diabetic patients who have a high risk of experiencing blindness in both eyes as defined by DRS criteria.
One eye of each patient is treated with laser photocoagulation. The hypothesis of interest is whether the laser treatment
delays the occurrence of blindness. Since juvenile and adult diabetes have very different courses, it is also desirable to
examine how the age of onset of diabetes might affect the time of blindness. Since there are no biological differences between
the left eye and the right eye, it is natural to assume a common baseline hazard function for the failure times of the left
and right eyes.
Each patient is a cluster that contributes two observations to the input data set, one for each eye. The following variables
are in the input data set Blind:
-
ID, patient’s identification -
Time, time to blindness -
Status, blindness indicator (0:censored and 1:blind) -
Treat, treatment received (Laser or Others) -
Type, type of diabetes (Juvenile: onset at age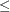 20 or Adult: onset at age > 20)
20 or Adult: onset at age > 20)
proc format; value type 0='Juvenile' 1='Adult'; value Rx 1='Laser' 0='Others'; run; data Blind; input ID Time Status dty trt @@; Type= put(dty, type.); Treat= put(trt, Rx.); datalines; 5 46.23 0 1 1 5 46.23 0 1 0 14 42.50 0 0 1 14 31.30 1 0 0 16 42.27 0 0 1 16 42.27 0 0 0 25 20.60 0 0 1 25 20.60 0 0 0 29 38.77 0 0 1 29 0.30 1 0 0 46 65.23 0 0 1 46 54.27 1 0 0 ... more lines ... 1705 8.00 0 0 1 1705 8.00 0 0 0 1717 51.60 0 1 1 1717 42.33 1 1 0 1727 49.97 0 1 1 1727 2.90 1 1 0 1746 45.90 0 0 1 1746 1.43 1 0 0 1749 41.93 0 1 1 1749 41.93 0 1 0 ;
As a preliminary analysis, PROC FREQ is used to summarize the number of eyes that developed blindness.
proc freq data=Blind; table Treat*Status; run;
By the end of the study, 54 eyes treated with laser photocoagulation and 101 eyes treated by other means have developed blindness (Output 71.11.1).
Output 71.11.1: Distribution of Blindness
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The following statements use PROC PHREG to carry out the analysis of Lee, Wei, and Amato (1992). The explanatory variables in this Cox model are Treat, Type, and the Treat ![]()
Type interaction. The COVS(AGGREGATE) option is specified to compute the robust sandwich covariance matrix estimate. The ID statement
identifies the variable that represents the clusters. The HAZARDRATIO statement requests hazard ratios for the treatments
be displayed.
proc phreg data=Blind covs(aggregate); class Treat Type; model Time*Status(0)=Treat|Type; id ID; hazardratio 'Marginal Model Analysis' Treat; run;
Results of the marginal model analysis are displayed in Output 71.11.2. The robust standard error estimates are smaller than the model-based counterparts, since the ratio of the robust standard error estimate relative to the model-based estimate is less than 1 for each parameter. Laser photocoagulation appears to be effective (p = 0.0217) in delaying the occurrence of blindness, although there is also a significant interaction effect between treatment and type of diabetes (p = 0.0053).
Output 71.11.2: Inference Based the Marginal Model
| Analysis of Maximum Likelihood Estimates | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Parameter Estimate |
Standard Error |
StdErr Ratio |
Chi-Square | Pr > ChiSq | Hazard Ratio |
Label | ||
| Treat | Laser | 1 | -0.42467 | 0.18497 | 0.850 | 5.2713 | 0.0217 | . | Treat Laser | |
| Type | Adult | 1 | 0.34084 | 0.19558 | 0.982 | 3.0371 | 0.0814 | . | Type Adult | |
| Treat*Type | Laser | Adult | 1 | -0.84566 | 0.30353 | 0.865 | 7.7622 | 0.0053 | . | Treat Laser * Type Adult |
Hazard ratio estimates of the laser treatment relative to nonlaser treatment are displayed in Output 71.11.3. For both types of diabetes, the 95% confidence interval for the hazard ratio lies below 1. This indicates that laser-photocoagulation treatment is more effective in delaying blindness regardless of the type of diabetes. However, the effect is more prominent for adult-onset diabetes than for juvenile-onset diabetes since the hazard ratio estimates for the former are less than those of the latter.
Output 71.11.3: Hazard Ratio Estimates for Marginal Model
| Marginal Model Analysis: Hazard Ratios for Treat | |||
|---|---|---|---|
| Description | Point Estimate | 95% Wald Robust Confidence Limits |
|
| Treat Laser vs Others At Type=Adult | 0.281 | 0.175 | 0.451 |
| Treat Laser vs Others At Type=Juvenile | 0.654 | 0.455 | 0.940 |
Next, you analyze the same data by using a shared frailty model. The following statements use PROC PHREG to fit a shared frailty
model to the Blind data set. The RANDOM statement identifies the variable ID as the variable that represents the clusters. You must declare the cluster variable as a classification variable in the CLASS
statement.
proc phreg data=Blind; class ID Treat Type; model Time*Status(0)=Treat|Type; random ID; hazardratio 'Frailty Model Analysis' Treat; run;
Selected results of this analysis are displayed in Output 71.11.4 to Output 71.11.6.
The “Random Class Level Information” table in Output 71.11.4 displays the 197 ID values of the patients. You can suppress the display of this table by using the NOCLPRINT option in the RANDOM statement.
Output 71.11.4: Unique Cluster Identification Values
| Class Level Information for Random Effects | ||
|---|---|---|
| Class | Levels | Values |
| ID | 197 | 5 14 16 25 29 46 49 56 61 71 100 112 120 127 133 150 167 176 185 190 202 214 220 243 255 264 266 284 295 300 302 315 324 328 335 342 349 357 368 385 396 405 409 419 429 433 445 454 468 480 485 491 503 515 522 538 547 550 554 557 561 568 572 576 581 606 610 615 618 624 631 636 645 653 662 664 683 687 701 706 717 722 731 740 749 757 760 766 769 772 778 780 793 800 804 810 815 832 834 838 857 866 887 903 910 920 925 931 936 945 949 952 962 964 971 978 983 987 1002 1017 1029 1034 1037 1042 1069 1074 1098 1102 1112 1117 1126 1135 1145 1148 1167 1184 1191 1205 1213 1228 1247 1250 1253 1267 1281 1287 1293 1296 1309 1312 1317 1321 1333 1347 1361 1366 1373 1397 1410 1413 1425 1447 1461 1469 1480 1487 1491 1499 1503 1513 1524 1533 1537 1552 1554 1562 1572 1581 1585 1596 1600 1603 1619 1627 1636 1640 1643 1649 1666 1672 1683 1688 1705 1717 1727 1746 1749 |
The “Covariance Parameter Estimates” table in Output 71.11.5 displays the estimate and asymptotic estimated standard error of the common variance parameter of the normal random effects.
Output 71.11.5: Variance Estimate of the Normal Random Effects
| Covariance Parameter Estimates | ||
|---|---|---|
| Cov Parm | REML Estimate | Standard Error |
| ID | 0.8308 | 0.2145 |
Output 71.11.6 displays the Wald tests for both the fixed effects and the random effects. The random effects are statistically significant (p = 0.0042). Results of testing the fixed effects are very similar to those based on the robust variance estimates. Laser photocoagulation appears to be effective (p = 0.0252) in delaying the occurrence of blindness, although there is also a significant treatment by diabetes type interaction effect (p = 0.0071).
Output 71.11.6: Inference Based on the Frailty Model
| Type 3 Tests | |||||
|---|---|---|---|---|---|
| Effect | Wald Chi-Square |
DF | Pr > ChiSq | Adjusted DF |
Adjusted Pr > ChiSq |
| Treat | 4.8964 | 1 | 0.0269 | 0.9587 | 0.0252 |
| Type | 2.6386 | 1 | 0.1043 | 0.6795 | 0.0629 |
| Treat*Type | 7.1336 | 1 | 0.0076 | 0.9644 | 0.0071 |
| ID | 110.3916 | . | . | 74.2776 | 0.0042 |
| Analysis of Maximum Likelihood Estimates | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | DF | Parameter Estimate |
Standard Error |
Chi-Square | Pr > ChiSq | Hazard Ratio |
Label | ||
| Treat | Laser | 1 | -0.49849 | 0.22528 | 4.8964 | 0.0269 | . | Treat Laser | |
| Type | Adult | 1 | 0.39781 | 0.24490 | 2.6386 | 0.1043 | . | Type Adult | |
| Treat*Type | Laser | Adult | 1 | -0.96530 | 0.36142 | 7.1336 | 0.0076 | . | Treat Laser * Type Adult |
Estimates of hazard ratios of the laser treatment relative to nonlaser treatment are displayed in Output 71.11.7. These estimates closely resemble those computed in analysis based on the marginal Cox model in Output 71.11.3, which leads to the same conclusion that laser photocoagulation is effective in delaying blindness for both types of diabetes, and more effective for the adult-onset diabetes than for juvenile-onset diabetes.
Output 71.11.7: Hazard Ratio Estimates for Frailty Model
| Frailty Model Analysis: Hazard Ratios for Treat | |||
|---|---|---|---|
| Description | Point Estimate | 95% Wald Confidence Limits | |
| Treat Laser vs Others At Type=Adult | 0.231 | 0.133 | 0.403 |
| Treat Laser vs Others At Type=Juvenile | 0.607 | 0.391 | 0.945 |