The PHREG Procedure
- Overview
-
Getting Started

-
Syntax
 PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement
PROC PHREG StatementASSESS StatementBASELINE StatementBAYES StatementBY StatementCLASS StatementCONTRAST StatementEFFECT StatementESTIMATE StatementFREQ StatementHAZARDRATIO StatementID StatementLSMEANS StatementLSMESTIMATE StatementMODEL StatementOUTPUT StatementProgramming StatementsRANDOM StatementSTRATA StatementSLICE StatementSTORE StatementTEST StatementWEIGHT Statement -
Details
 Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelProportional Rates/Means Models for Recurrent EventsThe Frailty ModelProportional Subdistribution Hazards Model for Competing-Risks DataHazard RatiosNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsSchemper-Henderson Predictive MeasureResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics
Failure Time DistributionTime and CLASS Variables UsagePartial Likelihood Function for the Cox ModelCounting Process Style of InputLeft-Truncation of Failure TimesThe Multiplicative Hazards ModelProportional Rates/Means Models for Recurrent EventsThe Frailty ModelProportional Subdistribution Hazards Model for Competing-Risks DataHazard RatiosNewton-Raphson MethodFirth’s Modification for Maximum Likelihood EstimationRobust Sandwich Variance EstimateTesting the Global Null HypothesisType 3 TestsConfidence Limits for a Hazard RatioUsing the TEST Statement to Test Linear HypothesesAnalysis of Multivariate Failure Time DataModel Fit StatisticsSchemper-Henderson Predictive MeasureResidualsDiagnostics Based on Weighted ResidualsInfluence of Observations on Overall Fit of the ModelSurvivor Function EstimatorsEffect Selection MethodsAssessment of the Proportional Hazards ModelThe Penalized Partial Likelihood Approach for Fitting Frailty ModelsSpecifics for Bayesian AnalysisComputational ResourcesInput and Output Data SetsDisplayed OutputODS Table NamesODS Graphics -
Examples
 Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential ModelAnalysis of Competing-Risks Data
Stepwise RegressionBest Subset SelectionModeling with Categorical PredictorsFirth’s Correction for Monotone LikelihoodConditional Logistic Regression for m:n MatchingModel Using Time-Dependent Explanatory VariablesTime-Dependent Repeated Measurements of a CovariateSurvival CurvesAnalysis of ResidualsAnalysis of Recurrent Events DataAnalysis of Clustered DataModel Assessment Using Cumulative Sums of Martingale ResidualsBayesian Analysis of the Cox ModelBayesian Analysis of Piecewise Exponential ModelAnalysis of Competing-Risks Data - References
Three estimators of the survivor function are available: the Breslow (1972) estimator, which is based on the empirical cumulative hazard function, the Fleming and Harrington (1984) estimator, which is a tie-breaking modification of the Breslow estimator, and the product-limit estimator (Kalbfleisch and Prentice, 1980, pp. 84–86).
Let ![]() be the distinct uncensored times of the survival data.
be the distinct uncensored times of the survival data.
To select this estimator, specify the METHOD=BRESLOW option in the BASELINE statement or OUTPUT statement. For the jth subject, let ![]() represent the failure time, the event indicator, and the vector of covariate values, respectively. For
represent the failure time, the event indicator, and the vector of covariate values, respectively. For ![]() , let
, let
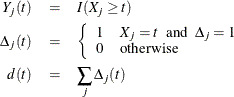
Note that ![]() is the number of subjects that have an event at t. Let
is the number of subjects that have an event at t. Let
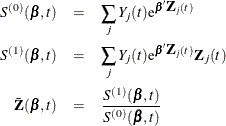
For a given realization of the explanatory variables ![]() , the cumulative hazard function estimator at
, the cumulative hazard function estimator at ![]() is
is
with variance estimated by
where
For the marginal model, the variance estimator computation follows Spiekerman and Lin (1998).
The Breslow estimate of the survivor function for ![]() is
is
By the delta method, the standard error of ![]() is approximated by
is approximated by
To select this estimator, specify the METHOD=FH option in the BASELINE statement or OUTPUT statement. With ![]() and
and ![]() as defined in the section Breslow Estimator and for
as defined in the section Breslow Estimator and for ![]() , let
, let
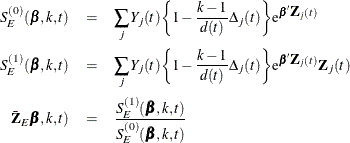
For a given realization of the explanatory variables, the Fleming-Harrington adjustment of the cumulative hazard function is
with variance estimated by
where
The Fleming-Harrington estimate of the survivor function for ![]() is
is
By the delta method, the standard error of ![]() is approximated by
is approximated by
To select this estimator, specify the METHOD=PL option in the BASELINE statement or OUTPUT statement. Let ![]() denote the set of individuals that fail at
denote the set of individuals that fail at ![]() . Let
. Let ![]() denote the set of individuals that are censored in the half-open interval
denote the set of individuals that are censored in the half-open interval ![]() , where
, where ![]() and
and ![]() . Let
. Let ![]() denote the censoring times in
denote the censoring times in ![]() , where l ranges over
, where l ranges over ![]() .
.
The likelihood function for all individuals is given by
where ![]() is empty. The likelihood
is empty. The likelihood ![]() is maximized by taking
is maximized by taking ![]() for
for ![]() and allowing the probability mass to fall only on the observed event times
and allowing the probability mass to fall only on the observed event times ![]() ,
, ![]() ,
, ![]() . By considering a discrete model with hazard contribution
. By considering a discrete model with hazard contribution ![]() at
at ![]() , you take
, you take ![]() , where
, where ![]() . Substitution into the likelihood function produces
. Substitution into the likelihood function produces
If you replace ![]() with
with ![]() estimated from the partial likelihood function and then maximize with respect to
estimated from the partial likelihood function and then maximize with respect to ![]() , the maximum likelihood estimate
, the maximum likelihood estimate ![]() of
of ![]() becomes a solution of
becomes a solution of
![\[ \sum _{ j \in \mc {D}_ i } \frac{ \mr {exp}(\mb {Z}_{j}\hat{\bbeta }) }{ 1-\hat{\alpha }_{i}^{ \ \mr {exp}(\mb {Z}_{j}\hat{\bbeta }) } } =\sum _{l \in \mc {R}_ i } \mr {exp}(\mb {Z}’_{l}\hat{\bbeta }) \]](images/statug_phreg0669.png)
When only a single failure occurs at ![]() ,
, ![]() can be found explicitly. Otherwise, an iterative solution is obtained by the Newton method.
can be found explicitly. Otherwise, an iterative solution is obtained by the Newton method.
The baseline survival function is estimated by
For a given realization of the explanatory variables ![]() , the product-limit estimate of the survival function at
, the product-limit estimate of the survival function at ![]() is
is
Approximating the variance of ![]() by the variance estimate of the Breslow estimator of the cumulative hazard function, the variance of the product-limit estimator
at
by the variance estimate of the Breslow estimator of the cumulative hazard function, the variance of the product-limit estimator
at ![]() is given by
is given by
Consider the Breslow estimator of the survival function. For ![]() , let
, let ![]() represent the covariate set of the jth patient. The direct adjusted survival curve averages the estimated survival curves for each patient:
represent the covariate set of the jth patient. The direct adjusted survival curve averages the estimated survival curves for each patient:
The variance of ![]() can be estimated by
can be estimated by
where
![\begin{eqnarray*} V^{(1)}(t)& =& \biggl ( \sum _{j=1}^ n \mr {e}^{\hat{\bbeta }\bxi _ j} \hat{S}(t,\bxi _ j) \biggr )^2 \sum _{t_ i\leq t} \frac{d(t_ i)}{[S^{(0)}(\hat{\bbeta },t_ i)]^2} \\ V^{(2)}(t)& =& \biggl (\sum _{j=1}^ n \hat{S}(t,\bxi _ j)H(t,\bxi _ j)\biggr )’ \biggl [\mc {I}(\hat{\bbeta }) \biggr ]^{-1} \biggl (\sum _{j=1}^ n \hat{S}(t,\bxi _ j) H(t,\bxi _ j) \biggr ) \end{eqnarray*}](images/statug_phreg0681.png)
For a stratified Cox model, let k index the strata. For the jth patient, let ![]() and
and ![]() be the estimated survival function and the
be the estimated survival function and the ![]() vector for the kth stratum. The direct adjusted survival curve for the kth stratum is
vector for the kth stratum. The direct adjusted survival curve for the kth stratum is
The variance of ![]() can be estimated by
can be estimated by
where
![\begin{eqnarray*} U^{(1)}_ k(t) & =& \left( \sum _{j=1}^ n \mr {e}^{\bbeta \bxi _{j}} \hat{S}_ k(t,\bxi _{j}) \right)^2 \sum _{t_ i\leq t} \frac{d(t_ i)}{[S^{(0)}(\hat{\bbeta },t_ i)]^2} \mbox{~ ~ ~ } k=1,2 \\ U^{(2)}_{12}(t)& =& \left\{ \sum _{j=1}^ n \left[\hat{S}_1(t,\bxi _{j})H_1(t,\bxi _{j})-\hat{S}_2(t,\bxi _{j})H_2(t,\bxi _{j}) \right] \right\} ^{\prime } \mc {I} ^{-1}(\hat{\bbeta }) \\ & & \left\{ \sum _{j=1}^ n \left[\hat{S}_1(t,\bxi _{j})H_2(t,\bxi _{j})-\hat{S}_1(t,\bxi _{j})H(_2t,\bxi _{j}) \right] \right\} \end{eqnarray*}](images/statug_phreg0688.png)
When the computation of confidence limits for the survivor function ![]() is based on the asymptotic normality of the survival estimator
is based on the asymptotic normality of the survival estimator ![]() —which can be the Breslow estimator
—which can be the Breslow estimator ![]() , the Fleming-Harrington estimator
, the Fleming-Harrington estimator ![]() , or the product-limit estimator
, or the product-limit estimator ![]() —the approximate confidence interval might include impossible values outside the range [0,1] at extreme values of t. This problem can be avoided by applying the asymptotic normality to a transformation of
—the approximate confidence interval might include impossible values outside the range [0,1] at extreme values of t. This problem can be avoided by applying the asymptotic normality to a transformation of ![]() for which the range is unrestricted. In addition, certain transformed confidence intervals for
for which the range is unrestricted. In addition, certain transformed confidence intervals for ![]() perform better than the usual linear confidence intervals (Borgan and Liestøl, 1990). The CLTYPE= option in the BASELINE statement enables you to choose one of the following transformations: the log-log function,
the log function, and the linear function.
perform better than the usual linear confidence intervals (Borgan and Liestøl, 1990). The CLTYPE= option in the BASELINE statement enables you to choose one of the following transformations: the log-log function,
the log function, and the linear function.
Let g be the transformation that is being applied to the survivor function ![]() . By the delta method, the standard error of
. By the delta method, the standard error of ![]() is estimated by
is estimated by
where ![]() is the first derivative of the function g. The 100(1–
is the first derivative of the function g. The 100(1–![]() )% confidence interval for
)% confidence interval for ![]() is given by
is given by
where ![]() is the inverse function of g. The choices for the transformation g are as follows:
is the inverse function of g. The choices for the transformation g are as follows:
-
CLTYPE=NORMAL specifies linear transformation, which is the same as having no transformation in which g is the identity. The 100(1–
 )% confidence interval for
)% confidence interval for 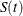 is given by
is given by
![\[ \hat{S}(t) - z_{\frac{\alpha }{2}}\hat{\sigma }\left[\hat{S}(t)\right] \le S(t) \le \hat{S}(t) + z_{\frac{\alpha }{2}}\hat{\sigma }\left[\hat{S}(t)\right] \]](images/statug_phreg0703.png)
-
CLTYPE=LOG specifies log transformation. The estimated variance of
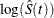 is
is 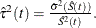 The 100(1–
The 100(1– )% confidence interval for
)% confidence interval for 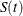 is given by
is given by
![\[ \hat{S}(t)\exp \left(-z_{\frac{\alpha }{2}}\hat{\tau }(t)\right) \le S(t) \le \hat{S}(t)\exp \left(z_{\frac{\alpha }{2}}\hat{\tau }(t)\right) \]](images/statug_phreg0706.png)
-
CLTYPE=LOGLOG specifies log-log transformation. The estimated variance of
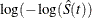 is
is ![$ \hat{\tau }^2(t) = \frac{\hat{\sigma }^2[\hat{S}(t)]}{ [\hat{S}(t)\log (\hat{S}(t))]^2 }. $](images/statug_phreg0708.png) The 100(1–
The 100(1– )% confidence interval for
)% confidence interval for 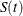 is given by
is given by
![\[ \left[\hat{S}(t)\right]^{\exp \left( z_{\frac{\alpha }{2}} \hat{\tau }(t)\right)} \le S(t) \le \left[\hat{S}(t)\right]^{\exp \left(-z_{\frac{\alpha }{2}} \hat{\tau }(t)\right)} \]](images/statug_phreg0709.png)
![\begin{eqnarray*} V^{(1)}_{12}(t) & =& \left\{ \sum _{j=1}^ n \left[\mr {e}^{\bbeta \bxi _{1j}} \hat{S}(t,\bxi _{1j}) - \mr {e}^{\bbeta \bxi _{2j}} \hat{S}(t,\bxi _{2j}) \right] \right\} ^2 \sum _{t_ i\leq t} \frac{d(t_ i)}{[S^{(0)}(\hat{\bbeta },t_ i)]^2} \\ V^{(2)}_{12}(t)& =& \left\{ \sum _{j=1}^ n \left[\hat{S}(t,\bxi _{1j})H(t,\bxi _{1j})-\hat{S}(t,\bxi _{2j})H(t,\bxi _{2j}) \right] \right\} ^{\prime } \mc {I} ^{-1}(\hat{\bbeta })\\ & & \left\{ \sum _{j=1}^ n \left[\hat{S}(t,\bxi _{1j})H(t,\bxi _{1j})-\hat{S}(t,\bxi _{2j})H(t,\bxi _{2j}) \right] \right\} \end{eqnarray*}](images/statug_phreg0693.png)