The MI Procedure
- Overview
- Getting Started
-
Syntax

-
Details
 Descriptive StatisticsEM Algorithm for Data with Missing ValuesStatistical Assumptions for Multiple ImputationMissing Data PatternsImputation MethodsMonotone Methods for Data Sets with Monotone Missing PatternsMonotone and FCS Regression MethodsMonotone and FCS Predictive Mean Matching MethodsMonotone and FCS Discriminant Function MethodsMonotone and FCS Logistic Regression MethodsMonotone Propensity Score MethodFCS Methods for Data Sets with Arbitrary Missing PatternsChecking Convergence in FCS MethodsMCMC Method for Arbitrary Missing Multivariate Normal DataProducing Monotone Missingness with the MCMC MethodMCMC Method SpecificationsChecking Convergence in MCMCInput Data SetsOutput Data SetsCombining Inferences from Multiply Imputed Data SetsMultiple Imputation EfficiencyImputer’s Model Versus Analyst’s ModelParameter Simulation versus Multiple ImputationSensitivity Analysis for the MAR AssumptionMultiple Imputation with Pattern-Mixture ModelsSpecifying Sets of Observations for Imputation in Pattern-Mixture ModelsAdjusting Imputed Values in Pattern-Mixture ModelsSummary of Issues in Multiple ImputationODS Table NamesODS Graphics
Descriptive StatisticsEM Algorithm for Data with Missing ValuesStatistical Assumptions for Multiple ImputationMissing Data PatternsImputation MethodsMonotone Methods for Data Sets with Monotone Missing PatternsMonotone and FCS Regression MethodsMonotone and FCS Predictive Mean Matching MethodsMonotone and FCS Discriminant Function MethodsMonotone and FCS Logistic Regression MethodsMonotone Propensity Score MethodFCS Methods for Data Sets with Arbitrary Missing PatternsChecking Convergence in FCS MethodsMCMC Method for Arbitrary Missing Multivariate Normal DataProducing Monotone Missingness with the MCMC MethodMCMC Method SpecificationsChecking Convergence in MCMCInput Data SetsOutput Data SetsCombining Inferences from Multiply Imputed Data SetsMultiple Imputation EfficiencyImputer’s Model Versus Analyst’s ModelParameter Simulation versus Multiple ImputationSensitivity Analysis for the MAR AssumptionMultiple Imputation with Pattern-Mixture ModelsSpecifying Sets of Observations for Imputation in Pattern-Mixture ModelsAdjusting Imputed Values in Pattern-Mixture ModelsSummary of Issues in Multiple ImputationODS Table NamesODS Graphics -
Examples
 EM Algorithm for MLEMonotone Propensity Score MethodMonotone Regression MethodMonotone Logistic Regression Method for CLASS VariablesMonotone Discriminant Function Method for CLASS VariablesFCS Method for Continuous VariablesFCS Method for CLASS VariablesFCS Method with Trace PlotMCMC MethodProducing Monotone Missingness with MCMCChecking Convergence in MCMCSaving and Using Parameters for MCMCTransforming to NormalityMultistage ImputationCreating Control-Based Pattern Imputation in Sensitivity AnalysisAdjusting Imputed Continuous Values in Sensitivity AnalysisAdjusting Imputed Classification Levels in Sensitivity AnalysisAdjusting Imputed Values with Parameters in a Data Set
EM Algorithm for MLEMonotone Propensity Score MethodMonotone Regression MethodMonotone Logistic Regression Method for CLASS VariablesMonotone Discriminant Function Method for CLASS VariablesFCS Method for Continuous VariablesFCS Method for CLASS VariablesFCS Method with Trace PlotMCMC MethodProducing Monotone Missingness with MCMCChecking Convergence in MCMCSaving and Using Parameters for MCMCTransforming to NormalityMultistage ImputationCreating Control-Based Pattern Imputation in Sensitivity AnalysisAdjusting Imputed Continuous Values in Sensitivity AnalysisAdjusting Imputed Classification Levels in Sensitivity AnalysisAdjusting Imputed Values with Parameters in a Data Set - References
The discriminant function method is the default imputation method in the MONOTONE and FCS statements for classification variables.
For a nominal classification variable ![]() with responses 1, …, g and a set of effects from its preceding variables, if the covariates
with responses 1, …, g and a set of effects from its preceding variables, if the covariates ![]() ,
, ![]() , …,
, …, ![]() associated with these effects within each group are approximately multivariate normal and the within-group covariance matrices
are approximately equal, the discriminant function method (Brand, 1999, pp. 95–96) can be used to impute missing values for the variable
associated with these effects within each group are approximately multivariate normal and the within-group covariance matrices
are approximately equal, the discriminant function method (Brand, 1999, pp. 95–96) can be used to impute missing values for the variable ![]() .
.
Denote the group-specific means for covariates ![]() ,
, ![]() , …,
, …, ![]() by
by
then the pooled covariance matrix is computed as
where ![]() is the within-group covariance matrix,
is the within-group covariance matrix, ![]() is the group-specific sample size, and
is the group-specific sample size, and ![]() is the total sample size.
is the total sample size.
In each imputation, new parameters of the group-specific means (![]() ), pooled covariance matrix (
), pooled covariance matrix (![]() ), and prior probabilities of group membership (
), and prior probabilities of group membership (![]() ) can be drawn from their corresponding posterior distributions (Schafer, 1997, p. 356).
) can be drawn from their corresponding posterior distributions (Schafer, 1997, p. 356).
For each imputation, the MI procedure uses either the fixed observed pooled covariance matrix (PCOV=FIXED) or a drawn pooled covariance matrix (PCOV=POSTERIOR) from its posterior distribution with a noninformative prior. That is,
where ![]() is an inverted Wishart distribution.
is an inverted Wishart distribution.
The group-specific means are then drawn from their posterior distributions with a noninformative prior
See the section Bayesian Estimation of the Mean Vector and Covariance Matrix for a complete description of the inverted Wishart distribution and posterior distributions that use a noninformative prior.
The prior probabilities are computed through the drawing of new group sample sizes. When the total sample size n is considered fixed, the group sample sizes ![]() have a multinomial distribution. New multinomial parameters (group sample sizes) can be drawn from their posterior distribution
by using a Dirichlet prior with parameters
have a multinomial distribution. New multinomial parameters (group sample sizes) can be drawn from their posterior distribution
by using a Dirichlet prior with parameters ![]() .
.
After the new sample sizes are drawn from the posterior distribution of ![]() , the prior probabilities
, the prior probabilities ![]() are computed proportionally to the drawn sample sizes.
are computed proportionally to the drawn sample sizes.
See Schafer (1997, pp. 247–255) for a complete description of the Dirichlet prior.
The discriminant function method uses the following steps in each imputation to impute values for a nominal classification
variable ![]() with g responses:
with g responses:
-
Draw a pooled covariance matrix
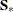 from its posterior distribution if the PCOV=POSTERIOR option is used.
from its posterior distribution if the PCOV=POSTERIOR option is used.
-
For each group, draw group means
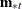 from the observed group mean
from the observed group mean 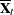 and either the observed pooled covariance matrix (PCOV=FIXED) or the drawn pooled covariance matrix
and either the observed pooled covariance matrix (PCOV=FIXED) or the drawn pooled covariance matrix 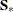 (PCOV=POSTERIOR).
(PCOV=POSTERIOR).
-
For each group, compute or draw
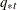 , prior probabilities of group membership, based on the PRIOR= option:
, prior probabilities of group membership, based on the PRIOR= option:
-
PRIOR=EQUAL,
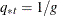 , prior probabilities of group membership are all equal.
, prior probabilities of group membership are all equal.
-
PRIOR=PROPORTIONAL,
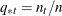 , prior probabilities are proportional to their group sample sizes.
, prior probabilities are proportional to their group sample sizes.
-
PRIOR=JEFFREYS=
 , a noninformative Dirichlet prior with
, a noninformative Dirichlet prior with 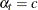 is used.
is used.
-
PRIOR=RIDGE=
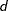 , a ridge prior is used with
, a ridge prior is used with 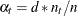 for
for 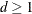 and
and 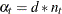 for
for 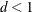 .
.
-
-
With the group means
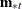 , the pooled covariance matrix
, the pooled covariance matrix 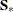 , and the prior probabilities of group membership
, and the prior probabilities of group membership 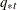 , the discriminant function method derives linear discriminant function and computes the posterior probabilities of an observation
belonging to each group
, the discriminant function method derives linear discriminant function and computes the posterior probabilities of an observation
belonging to each group
![\[ p_{t}(\mb {x}) = \frac{ \mr {exp}(-0.5 D_{t}^{2}(\mb {x}) )}{ \sum _{u=1}^{g} \mr {exp}(-0.5 D_{u}^{2}(\mb {x}) )} \]](images/statug_mi0143.png)
where
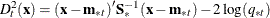 is the generalized squared distance from
is the generalized squared distance from  to group t.
to group t.
-
Draw a random uniform variate u, between 0 and 1, for each observation with missing group value. With the posterior probabilities,
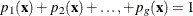 , the discriminant function method imputes
, the discriminant function method imputes 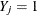 if the value of u is less than
if the value of u is less than  ,
, 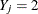 if the value is greater than or equal to
if the value is greater than or equal to 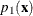 but less than
but less than 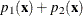 , and so on.
, and so on.