The MCMC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics
Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics - References
You can use the Poisson distribution to model the distribution of cell counts in a multiway contingency table. Aitkin et al. (1989) have used this method to model insurance claims data. Suppose the following hypothetical insurance claims data are classified by two factors: age group (with two levels) and car type (with three levels). The following statements create the data set:
title 'Poisson Regression'; data insure; input n c car $ age; ln = log(n); datalines; 500 42 small 0 1200 37 medium 0 100 1 large 0 400 101 small 1 500 73 medium 1 300 14 large 1 ; proc transreg data=insure design; model class(car / zero=last); id n c age ln; output out=input_insure(drop=_: Int:); run;
The variable n represents the number of insurance policy holders and the variable c represents the number of insurance claims. The variable car is the type of car involved (classified into three groups), and it is coded into two levels. The variable age is the age group of a policy holder (classified into two groups).
Assume that the number of claims c has a Poisson probability distribution and that its mean, ![]() , is related to the factors
, is related to the factors car and age for observation i by
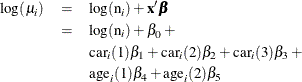
The indicator variables ![]() is associated with the jth level of the variable
is associated with the jth level of the variable car for observation i in the following way:
A similar coding applies to age. The ![]() ’s are parameters. The logarithm of the variable
’s are parameters. The logarithm of the variable n is used as an offset—that is, a regression variable with a constant coefficient of 1 for each observation. Having the offset
constant in the model is equivalent to fitting an expanded data set with 3000 observations, each with response variable y observed on an individual level. The log link relates the mean and the factors car and age.
The following statements run PROC MCMC:
proc mcmc data=input_insure outpost=insureout nmc=5000 propcov=quanew
maxtune=0 seed=7;
ods select PostSumInt;
array data[4] 1 &_trgind age;
array beta[4] alpha beta_car1 beta_car2 beta_age;
parms alpha beta:;
prior alpha beta: ~ normal(0, prec = 1e-6);
call mult(data, beta, mu);
model c ~ poisson(exp(mu+ln));
run;
The analysis uses a relatively flat prior on all the regression coefficients, with mean at 0 and precision at ![]() . The option MAXTUNE=0 skips the tuning phase because the optimization routine (PROPCOV=QUANEW) provides good initial values and proposal covariance matrix.
. The option MAXTUNE=0 skips the tuning phase because the optimization routine (PROPCOV=QUANEW) provides good initial values and proposal covariance matrix.
There are four parameters in the model: alpha is the intercept; beta_car1 and beta_car2 are coefficients for the CLASS variable car, which has three levels; and beta_age is the coefficient for age. The symbol mu connects the regression model and the Poisson mean by using the log link. The MODEL statement specifies a Poisson likelihood for the response variable c.
Posterior summary and interval statistics are shown in Output 59.5.1.
Output 59.5.1: MCMC Results
| Poisson Regression |
| Posterior Summaries and Intervals | |||||
|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
95% HPD Interval | |
| alpha | 5000 | -2.6403 | 0.1344 | -2.9133 | -2.3831 |
| beta_car1 | 5000 | -1.8335 | 0.2917 | -2.4692 | -1.3336 |
| beta_car2 | 5000 | -0.6931 | 0.1255 | -0.9485 | -0.4589 |
| beta_age | 5000 | 1.3151 | 0.1386 | 1.0387 | 1.5812 |
To fit the same model by using PROC GENMOD, you can do the following. Note that the default normal prior on the coefficients
![]() is
is ![]() , the same as used in the PROC MCMC. The following statements run PROC GENMOD and create Output 59.5.2:
, the same as used in the PROC MCMC. The following statements run PROC GENMOD and create Output 59.5.2:
proc genmod data=insure; ods select PostSummaries PostIntervals; class car age(descending); model c = car age / dist=poisson link=log offset=ln; bayes seed=17 nmc=5000 coeffprior=normal; run;
To compare, posterior summary and interval statistics from PROC GENMOD are reported in Output 59.5.2, and they are very similar to PROC MCMC results in Output 59.5.1.
Output 59.5.2: PROC GENMOD Results
| Poisson Regression |
| Posterior Summaries | ||||||
|---|---|---|---|---|---|---|
| Parameter | N | Mean | Standard Deviation |
Percentiles | ||
| 25% | 50% | 75% | ||||
| Intercept | 5000 | -2.6424 | 0.1336 | -2.7334 | -2.6391 | -2.5547 |
| carlarge | 5000 | -1.8040 | 0.2764 | -1.9859 | -1.7929 | -1.6101 |
| carmedium | 5000 | -0.6908 | 0.1311 | -0.7797 | -0.6898 | -0.6044 |
| age1 | 5000 | 1.3207 | 0.1384 | 1.2264 | 1.3209 | 1.4140 |
| Posterior Intervals | |||||
|---|---|---|---|---|---|
| Parameter | Alpha | Equal-Tail Interval | HPD Interval | ||
| Intercept | 0.050 | -2.9154 | -2.3893 | -2.8997 | -2.3850 |
| carlarge | 0.050 | -2.3668 | -1.2891 | -2.2992 | -1.2378 |
| carmedium | 0.050 | -0.9437 | -0.4231 | -0.9434 | -0.4230 |
| age1 | 0.050 | 1.0455 | 1.5871 | 1.0266 | 1.5629 |
Note that the descending option in the CLASS statement reverses the sort order of the CLASS variable age so that the results agree with PROC MCMC. If this option is not used, the estimate for age has a reversed sign as compared to Output 59.5.2.