The MCMC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics
Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics - References
The MCMC procedure provides you with a number of CALL routines for performing simple matrix operations on declared arrays. With the exception of FILLMATRIX, IDENTITY, and ZEROMATRIX, the CALL routines listed in Table 59.43 do not support matrices or arrays that contain missing values.
Table 59.43: Matrix Functions in PROC MCMC
|
CALL Routine |
Description |
|---|---|
|
Performs an element-wise addition of two matrices or of a matrix and a scalar. |
|
|
Calculates the Cholesky decomposition for a particular symmetric matrix. |
|
|
Calculates the determinant of a specified matrix, which must be square. |
|
|
Performs an element-wise multiplication of two matrices. |
|
|
Replaces all of the element values of the input matrix with the specified value. You can use this routine with multidimensional numeric arrays. |
|
|
Converts the input matrix to an identity matrix. Diagonal element values of the matrix are set to 1, and the rest of the values are set to 0. |
|
|
Calculates a matrix that is the inverse of the input matrix. The input matrix must be a square, nonsingular matrix. |
|
|
Calculates the matrix product of two input matrices. |
|
|
Performs an element-wide subtraction of two matrices or of a matrix and a scalar. |
|
|
Returns the transpose of a matrix. |
|
|
Replaces all of the element values of the numeric input matrix with 0. |
The ADDMATRIX CALL routine performs an element-wise addition of two matrices or of a matrix and a scalar.
The syntax of the ADDMATRIX CALL routine is
CALL ADDMATRIX (X, Y, Z) ;
where
-
X specifies a scalar or an input matrix with dimensions
 (that is, X[
(that is, X[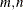 ])
])
-
Y specifies a scalar or an input matrix with dimensions
 (that is, Y[
(that is, Y[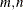 ])
])
-
Z specifies an output matrix with dimensions
 (that is, Z[
(that is, Z[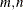 ])
])
such that
The CHOL CALL routine calculates the Cholesky decomposition for a particular symmetric matrix.
The syntax of the CHOL CALL routine is
CALL CHOL (X, Y <, validate>) ;
where
-
X specifies a symmetric positive-definite input matrix with dimensions
 (that is, X[m, m])
(that is, X[m, m])
-
Y is a variable that contains the Cholesky decomposition and specifies an output matrix with dimensions
 (that is, Y[
(that is, Y[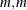 ])
])
-
validate specifies an optional argument that can increase the processing speed by avoiding error checking:
-
If validate = 0 or is not specified, then the matrix X is checked for symmetry.
-
If validate = 1, then the matrix X is assumed to be symmetric.
-
such that
where Y is a lower triangular matrix with strictly positive diagonal entries and Y![]() denotes the conjugate transpose of Y.
denotes the conjugate transpose of Y.
Both input and output matrices must be square and have the same dimensions. If X is symmetric positive-definite, Y is a lower triangle matrix. If X is not symmetric positive-definite, Y is filled with missing values.
The determinant, the product of the eigenvalues, is a single numeric value. If the determinant of a matrix is zero, then that matrix is singular (that is, it does not have an inverse). The routine performs an LU decomposition and collects the product of the diagonals.
The syntax of the DET CALL routine is
CALL DET (X, a) ;
where
-
X specifies an input matrix with dimensions
 (that is, X[
(that is, X[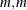 ])
])
-
a specifies the returned determinate value
such that
The ELEMMULT CALL routine performs an element-wise multiplication of two matrices.
The syntax of the ELEMMULT CALL routine is
CALL ELEMMULT (X, Y, Z) ;
where
-
X specifies an input matrix with dimensions
 (that is, X[
(that is, X[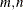 ])
])
-
Y specifies an input matrix with dimensions
 (that is, Y[
(that is, Y[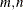 ])
])
-
Z specifies an output matrix with dimensions
 (that is, Z[
(that is, Z[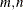 ])
])
The FILLMATRIX CALL routine replaces all of the element values of the input matrix with the specified value. You can use the FILLMATRIX CALL routine with multidimensional numeric arrays.
The syntax of the FILLMATRIX CALL routine is
CALL FILLMATRIX (X, Y) ;
where
-
X specifies an input numeric matrix
-
Y specifies the numeric value that is used to fill the matrix
The IDENTITY CALL routine converts the input matrix to an identity matrix. Diagonal element values of the matrix are set to 1, and the rest of the values are set to 0.
The syntax of the IDENTITY CALL routine is
CALL IDENTITY (X) ;
where
-
X specifies an input matrix with dimensions
 (that is, X[
(that is, X[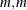 ])
])
The INV CALL routine calculates a matrix that is the inverse of the input matrix. The input matrix must be a square, nonsingular matrix.
The syntax of the INV CALL routine is
CALL INV (X, Y) ;
where
-
X specifies an input matrix with dimensions
 (that is, X[
(that is, X[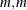 ])
])
-
Y specifies an output matrix with dimensions
 (that is, Y[
(that is, Y[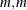 ])
])
The MULT CALL routine calculates the matrix product of two input matrices.
The syntax of the MULT CALL routine is
CALL MULT (X, Y, Z) ;
where
-
X specifies an input matrix with dimensions
 (that is, X[
(that is, X[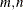 ])
])
-
Y specifies an input matrix with dimensions
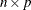 (that is, Y[
(that is, Y[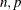 ])
])
-
Z specifies an output matrix with dimensions
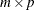 (that is, Z[
(that is, Z[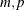 ])
])
The number of columns for the first input matrix must be the same as the number of rows for the second matrix. The calculated matrix is the last argument.
The SUBTRACTMATRIX CALL routine performs an element-wide subtraction of two matrices or of a matrix and a scalar.
The syntax of the SUBTRACTMATRIX CALL routine is
CALL SUBTRACTMATRIX (X, Y, Z) ;
where
-
X specifies a scalar or an input matrix with dimensions
 (that is, X[
(that is, X[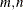 ])
])
-
Y specifies a scalar or an input matrix with dimensions
 (that is, Y[
(that is, Y[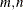 ])
])
-
Z specifies an output matrix with dimensions
 (that is, Z[
(that is, Z[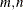 ])
])
such that
The TRANSPOSE CALL routine returns the transpose of a matrix.
The syntax of the TRANSPOSE CALL routine is
CALL TRANSPOSE (X, Y) ;
where
-
X specifies an input matrix with dimensions
 (that is, X[
(that is, X[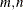 ])
])
-
Y specifies an output matrix with dimensions
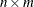 (that is, Y[
(that is, Y[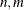 ])
])
The ZEROMATRIX CALL routine replaces all of the element values of the numeric input matrix with 0. You can use the ZEROMATRIX CALL routine with multidimensional numeric arrays.
The syntax of the ZEROMATRIX CALL routine is
CALL ZEROMATRIX (X) ;
where
-
X specifies a numeric input matrix.