Example 97.5 Metric Conjoint Analysis of Tire Data
This example, which is more detailed than the previous one, uses PROC TRANSREG to perform a metric conjoint analysis of tire preference data. Conjoint analysis can be used to decompose preference ratings of products or services
into components based on qualitative product attributes. For each level of each attribute of interest, a numerical “part-worth utility” value is computed. The sum of the part-worth utilities for each product is an estimate of the utility for that product. The
goal is to compute part-worth utilities such that the product utilities are as similar as possible to the original ratings. Metric conjoint analysis,
as shown in this example, fits an ordinary linear model directly to data assumed to be measured on an interval scale. Nonmetric
conjoint analysis, as shown in Example 97.4, finds an optimal monotonic transformation of original data before fitting an ordinary linear model to the transformed data.
This example has three parts. In the first part, an experimental design is created. In the second part, a DATA step creates
descriptions of the stimuli for the experiment. The third part of the example performs the conjoint analyses.
The stimuli for the experiment are 18 hypothetical tires. The stimuli represent different brands (Goodstone, Pirogi, Machismo), prices ($69.99, $74.99, $79.99), expected tread life (50,000, 60,000, 70,000 miles), and road hazard insurance plans (Yes,
No).
For a conjoint study such as this, you need to create an experimental design with 3 three-level factors, 1 two-level factor,
and 18 combinations or runs. The easiest way to get this design is with the %MktEx autocall macro. The %MktEx macro requires you to specify the number
of levels of each of the four factors, followed by N=18, the number of runs. Specifying a random number seed, while not strictly
necessary, helps ensure that the design is reproducible. The %MktLab macro assigns the actual factor names instead of the
default names x1, x2, and so on, and it assigns formats to the factor levels. The %MktEval macro helps you evaluate the design. It shows how correlated
or independent the factors are, how often each factor level appears in the design, how often each pair occurs for every factor
pair, and how often each product profile or run occurs in the design. See Kuhfeld (2010) for more information about experimental design and conjoint analysis; look for the latest “Conjoint Analysis” report. The following statements create, evaluate, and display the design:
title 'Tire Study, Experimental Design';
proc format;
value BrandF
1 = 'Goodstone'
2 = 'Pirogi '
3 = 'Machismo ';
value PriceF
1 = '$69.99'
2 = '$74.99'
3 = '$79.99';
value LifeF
1 = '50,000'
2 = '60,000'
3 = '70,000';
value HazardF
1 = 'Yes'
2 = 'No ';
run;
%mktex(3 3 3 2, n=18, seed=448)
%mktlab(vars=Brand Price Life Hazard, out=sasuser.TireDesign,
statements=format Brand BrandF9. Price PriceF9.
Life LifeF6. Hazard HazardF3.)
%mkteval;
proc print data=sasuser.TireDesign;
run;
The %MktEx macro (Kuhfeld, 2010) output displayed in Output 97.5.1 shows you that the design is 100% efficient, which means it is orthogonal and balanced. The %MktEval macro output displayed
in Output 97.5.2 shows you that all of the factors are uncorrelated or orthogonal, the design is balanced (each level occurs once), and every
pair of factor levels occurs equally often (again showing that the design is orthogonal). The n-way frequencies show that each product profile occurs once (there are no duplicates). The design is shown in Output 97.5.3. The design is automatically randomized (the profiles were sorted into a random order and the original levels are randomly
reassigned). Orthogonality, balance, randomization, and other design concepts are discussed in detail in Kuhfeld (2010), in the “Experimental Design, Efficiency, Coding, and Choice Designs” report.
Output 97.5.1: Tire Study, Design Efficiency
Current Best
Design Row,Col D-Efficiency D-Efficiency Notes
----------------------------------------------------------
1 Start 100.0000 100.0000 Tab
1 End 100.0000
|
The OPTEX Procedure
Class Level Information
Class Levels Values
x1 3 1 2 3
x2 3 1 2 3
x3 3 1 2 3
x4 2 1 2
|
| 100.0000 |
100.0000 |
100.0000 |
0.6667 |
Output 97.5.2: Tire Study, Design Evaluation
| 1 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
1 |
| 6 6 6 |
| 6 6 6 |
| 6 6 6 |
| 9 9 |
| 2 2 2 2 2 2 2 2 2 |
| 2 2 2 2 2 2 2 2 2 |
| 3 3 3 3 3 3 |
| 2 2 2 2 2 2 2 2 2 |
| 3 3 3 3 3 3 |
| 3 3 3 3 3 3 |
| 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 |
Output 97.5.3: Tire Study, Design
| Pirogi |
$79.99 |
50,000 |
No |
| Machismo |
$79.99 |
60,000 |
No |
| Machismo |
$74.99 |
70,000 |
Yes |
| Machismo |
$74.99 |
50,000 |
No |
| Goodstone |
$74.99 |
60,000 |
Yes |
| Pirogi |
$69.99 |
60,000 |
Yes |
| Goodstone |
$69.99 |
50,000 |
Yes |
| Machismo |
$69.99 |
50,000 |
Yes |
| Pirogi |
$74.99 |
60,000 |
Yes |
| Pirogi |
$74.99 |
50,000 |
No |
| Goodstone |
$79.99 |
60,000 |
No |
| Goodstone |
$69.99 |
70,000 |
No |
| Pirogi |
$79.99 |
70,000 |
Yes |
| Goodstone |
$74.99 |
70,000 |
No |
| Machismo |
$69.99 |
60,000 |
No |
| Machismo |
$79.99 |
70,000 |
Yes |
| Pirogi |
$69.99 |
70,000 |
No |
| Goodstone |
$79.99 |
50,000 |
Yes |
The %MktEx macro requires SAS/STAT, SAS/QC, and SAS/IML software. Alternatively, you can make a design for this experiment
using the %MktDes macro, which requires only SAS/STAT and SAS/QC software. The %MktDes macro contains a small subset of the
functionality of the %MktEx macro. It can be used as follows:
%mktdes(factors=Brand=3 Price=3 Life=3 Hazard=2, n=18)
The results of this step are not shown or used.
Next, the questionnaires are printed and given to the subjects, who are asked to rate the tires.
The following statements produce Output 97.5.4:
data _null_;
title;
set sasuser.TireDesign;
file print;
if mod(_n_,4) eq 1 then do;
put _page_;
put +55 'Subject ________';
end;
length hazardstring $ 7.;
if put(hazard, hazardf3.) = 'Yes'
then hazardstring = 'with';
else hazardstring = 'without';
s = 3 + (_n_ >= 10);
put // _n_ +(-1) ') For your next tire purchase, '
'how likely are you to buy this product?'
// +s Brand 'brand tires at ' Price +(-1) ','
/ +s 'with a ' Life 'tread life guarantee, '
/ +s 'and ' hazardstring 'road hazard insurance.'
// +s 'Definitely Would Definitely Would'
/ +s 'Not Purchase Purchase'
// +s '1 2 3 4 5 6 7 8 9 ';
run;
This output in Output 97.5.4 is abbreviated in the interest of conserving space; the statements actually produce stimuli for all combinations.
Output 97.5.4: Conjoint Analysis, Stimuli Descriptions
Subject ________
1) For your next tire purchase, how likely are you to buy this product?
Pirogi brand tires at $79.99,
with a 50,000 tread life guarantee,
and without road hazard insurance.
Definitely Would Definitely Would
Not Purchase Purchase
1 2 3 4 5 6 7 8 9
2) For your next tire purchase, how likely are you to buy this product?
Machismo brand tires at $79.99,
with a 60,000 tread life guarantee,
and without road hazard insurance.
Definitely Would Definitely Would
Not Purchase Purchase
1 2 3 4 5 6 7 8 9
3) For your next tire purchase, how likely are you to buy this product?
Machismo brand tires at $74.99,
with a 70,000 tread life guarantee,
and with road hazard insurance.
Definitely Would Definitely Would
Not Purchase Purchase
1 2 3 4 5 6 7 8 9
4) For your next tire purchase, how likely are you to buy this product?
Machismo brand tires at $74.99,
with a 50,000 tread life guarantee,
and without road hazard insurance.
Definitely Would Definitely Would
Not Purchase Purchase
1 2 3 4 5 6 7 8 9
|
The third part of the example performs the conjoint analyses. The DATA step reads the data. Only the ratings are entered,
one row per subject. Real conjoint studies have many more subjects than five. The TRANSPOSE procedure transposes this (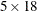 ) data set into an (
) data set into an (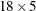 ) data set that can be merged with the factor level data set
) data set that can be merged with the factor level data set sasuser.TireDesign. The next DATA step does the merge. The PRINT procedure displays the input data set.
PROC TRANSREG fits the five individual conjoint models, one for each subject. The UTILITIES a-option displays the conjoint analysis results. The SHORT a-option suppresses the iteration histories, OUTTEST=UTILS creates an output data set with all of the conjoint results, and the SEPARATORS= option requests that the labels constructed for each category contain two blanks between the variable name and the level
value. The ODS SELECT statement is used to limit the displayed output. The MODEL statement specifies IDENTITY for the ratings, which specifies a metric conjoint analysis—the ratings are not transformed. The variables Brand, Price, Life, and Hazard are designated as CLASS variables, and the part-worth utilities are constrained to sum to zero within each factor.
The following statements produce Output 97.5.5:
title 'Tire Study, Data Entry, Preprocessing';
data Results;
input (c1-c18) (1.);
datalines;
233279766526376493
124467885349168274
262189456534275794
184396375364187754
133379775526267493
;
* Create an Object by Subject Data Matrix;
proc transpose data=Results out=Results(drop=_name_) prefix=Subj;
run;
* Merge the Factor Levels with the Data Matrix;
data Both;
merge sasuser.TireDesign Results;
run;
proc print;
title2 'Data Set for Conjoint Analysis';
run;
title 'Tire Study, Individual Conjoint Analyses';
* Fit Each Subject Individually;
proc transreg data=Both utilities short outtest=utils separators=' ';
ods select TestsNote FitStatistics Utilities;
model identity(Subj1-Subj5) =
class(Brand Price Life Hazard / zero=sum);
run;
The output contains two tables per subject, one with overall fit statistics and one with the conjoint analysis results.
Output 97.5.5: Conjoint Analysis
| Pirogi |
$79.99 |
50,000 |
No |
2 |
1 |
2 |
1 |
1 |
| Machismo |
$79.99 |
60,000 |
No |
3 |
2 |
6 |
8 |
3 |
| Machismo |
$74.99 |
70,000 |
Yes |
3 |
4 |
2 |
4 |
3 |
| Machismo |
$74.99 |
50,000 |
No |
2 |
4 |
1 |
3 |
3 |
| Goodstone |
$74.99 |
60,000 |
Yes |
7 |
6 |
8 |
9 |
7 |
| Pirogi |
$69.99 |
60,000 |
Yes |
9 |
7 |
9 |
6 |
9 |
| Goodstone |
$69.99 |
50,000 |
Yes |
7 |
8 |
4 |
3 |
7 |
| Machismo |
$69.99 |
50,000 |
Yes |
6 |
8 |
5 |
7 |
7 |
| Pirogi |
$74.99 |
60,000 |
Yes |
6 |
5 |
6 |
5 |
5 |
| Pirogi |
$74.99 |
50,000 |
No |
5 |
3 |
5 |
3 |
5 |
| Goodstone |
$79.99 |
60,000 |
No |
2 |
4 |
3 |
6 |
2 |
| Goodstone |
$69.99 |
70,000 |
No |
6 |
9 |
4 |
4 |
6 |
| Pirogi |
$79.99 |
70,000 |
Yes |
3 |
1 |
2 |
1 |
2 |
| Goodstone |
$74.99 |
70,000 |
No |
7 |
6 |
7 |
8 |
6 |
| Machismo |
$69.99 |
60,000 |
No |
6 |
8 |
5 |
7 |
7 |
| Machismo |
$79.99 |
70,000 |
Yes |
4 |
2 |
7 |
7 |
4 |
| Pirogi |
$69.99 |
70,000 |
No |
9 |
7 |
9 |
5 |
9 |
| Goodstone |
$79.99 |
50,000 |
Yes |
3 |
4 |
4 |
4 |
3 |
The TRANSREG Procedure
The TRANSREG Procedure Hypothesis Tests for Identity(Subj1)
| 1.34164 |
0.8043 |
| 5.00000 |
0.6674 |
| 26.83282 |
|
| 5.0000 |
0.31623 |
|
Intercept |
| 0.3333 |
0.44721 |
20.833 |
Class.BrandGoodstone |
| 0.6667 |
0.44721 |
|
Class.BrandPirogi |
| -1.0000 |
0.44721 |
|
Class.BrandMachismo |
| 2.1667 |
0.44721 |
54.167 |
Class.Price_69_99 |
| 0.0000 |
0.44721 |
|
Class.Price_74_99 |
| -2.1667 |
0.44721 |
|
Class.Price_79_99 |
| -0.8333 |
0.44721 |
16.667 |
Class.Life50_000 |
| 0.5000 |
0.44721 |
|
Class.Life60_000 |
| 0.3333 |
0.44721 |
|
Class.Life70_000 |
| 0.3333 |
0.31623 |
8.333 |
Class.HazardYes |
| -0.3333 |
0.31623 |
|
Class.HazardNo |
The TRANSREG Procedure
The TRANSREG Procedure Hypothesis Tests for Identity(Subj2)
| 0.56765 |
0.9710 |
| 4.94444 |
0.9506 |
| 11.48049 |
|
| 4.9444 |
0.13380 |
|
Intercept |
| 1.2222 |
0.18922 |
25.658 |
Class.BrandGoodstone |
| -0.9444 |
0.18922 |
|
Class.BrandPirogi |
| -0.2778 |
0.18922 |
|
Class.BrandMachismo |
| 2.8889 |
0.18922 |
65.132 |
Class.Price_69_99 |
| -0.2778 |
0.18922 |
|
Class.Price_74_99 |
| -2.6111 |
0.18922 |
|
Class.Price_79_99 |
| -0.2778 |
0.18922 |
7.895 |
Class.Life50_000 |
| 0.3889 |
0.18922 |
|
Class.Life60_000 |
| -0.1111 |
0.18922 |
|
Class.Life70_000 |
| 0.0556 |
0.13380 |
1.316 |
Class.HazardYes |
| -0.0556 |
0.13380 |
|
Class.HazardNo |
The TRANSREG Procedure
The TRANSREG Procedure Hypothesis Tests for Identity(Subj3)
| 2.48104 |
0.3902 |
| 4.94444 |
-0.0367 |
| 50.17832 |
|
| 4.9444 |
0.58479 |
|
Intercept |
| 0.0556 |
0.82701 |
18.261 |
Class.BrandGoodstone |
| 0.5556 |
0.82701 |
|
Class.BrandPirogi |
| -0.6111 |
0.82701 |
|
Class.BrandMachismo |
| 1.0556 |
0.82701 |
31.304 |
Class.Price_69_99 |
| -0.1111 |
0.82701 |
|
Class.Price_74_99 |
| -0.9444 |
0.82701 |
|
Class.Price_79_99 |
| -1.4444 |
0.82701 |
41.739 |
Class.Life50_000 |
| 1.2222 |
0.82701 |
|
Class.Life60_000 |
| 0.2222 |
0.82701 |
|
Class.Life70_000 |
| 0.2778 |
0.58479 |
8.696 |
Class.HazardYes |
| -0.2778 |
0.58479 |
|
Class.HazardNo |
The TRANSREG Procedure
The TRANSREG Procedure Hypothesis Tests for Identity(Subj4)
| 1.90321 |
0.6185 |
| 5.05556 |
0.3514 |
| 37.64598 |
|
| 5.0556 |
0.44859 |
|
Intercept |
| 0.6111 |
0.63440 |
36.885 |
Class.BrandGoodstone |
| -1.5556 |
0.63440 |
|
Class.BrandPirogi |
| 0.9444 |
0.63440 |
|
Class.BrandMachismo |
| 0.2778 |
0.63440 |
12.295 |
Class.Price_69_99 |
| 0.2778 |
0.63440 |
|
Class.Price_74_99 |
| -0.5556 |
0.63440 |
|
Class.Price_79_99 |
| -1.5556 |
0.63440 |
49.180 |
Class.Life50_000 |
| 1.7778 |
0.63440 |
|
Class.Life60_000 |
| -0.2222 |
0.63440 |
|
Class.Life70_000 |
| 0.0556 |
0.44859 |
1.639 |
Class.HazardYes |
| -0.0556 |
0.44859 |
|
Class.HazardNo |
The TRANSREG Procedure
The TRANSREG Procedure Hypothesis Tests for Identity(Subj5)
| 1.36219 |
0.8162 |
| 4.94444 |
0.6875 |
| 27.54987 |
|
| 4.9444 |
0.32107 |
|
Intercept |
| 0.2222 |
0.45406 |
9.023 |
Class.BrandGoodstone |
| 0.2222 |
0.45406 |
|
Class.BrandPirogi |
| -0.4444 |
0.45406 |
|
Class.BrandMachismo |
| 2.5556 |
0.45406 |
67.669 |
Class.Price_69_99 |
| -0.1111 |
0.45406 |
|
Class.Price_74_99 |
| -2.4444 |
0.45406 |
|
Class.Price_79_99 |
| -0.6111 |
0.45406 |
15.789 |
Class.Life50_000 |
| 0.5556 |
0.45406 |
|
Class.Life60_000 |
| 0.0556 |
0.45406 |
|
Class.Life70_000 |
| 0.2778 |
0.32107 |
7.519 |
Class.HazardYes |
| -0.2778 |
0.32107 |
|
Class.HazardNo |
The next steps summarize the results. Three tables are displayed, showing the following: all of the importance values, the
average importance, and the part-worth utilities. The first DATA step selects the importance information from the UTILS data set. The final assignment statement stores just the variable name from the label, relying on the fact that the separator
is two blanks. PROC TRANSPOSE creates the data set of importances, one row per subject, and PROC PRINT displays the results.
The MEANS procedure displays the average importance of each attribute across the subjects. The next DATA step selects the
part-worth utilities information from the UTILS data set. PROC TRANSPOSE creates the data set of utilities, one row per subject, and PROC PRINT displays the results. The
following statements produce Output 97.5.6:
title 'Tire Study Results';
* Gather the Importance Values;
data Importance;
set utils(keep=_depvar_ Importance Label);
if n(Importance);
label = substr(label, 1, index(label, ' '));
run;
proc transpose out=Importance2(drop=_:);
by _depvar_;
id Label;
run;
proc print;
title2 'Importance Values';
run;
proc means;
title2 'Average Importance';
run;
* Gather the Part-Worth Utilities;
data Utilities;
set utils(keep=_depvar_ Coefficient Label);
if n(Coefficient);
run;
proc transpose out=Utilities2(drop=_:);
by _depvar_;
id Label;
idlabel Label;
run;
proc print label;
title2 'Utilities';
run;
Output 97.5.6: Summary of Conjoint Analysis Results
| 20.8333 |
54.1667 |
16.6667 |
8.33333 |
| 25.6579 |
65.1316 |
7.8947 |
1.31579 |
| 18.2609 |
31.3043 |
41.7391 |
8.69565 |
| 36.8852 |
12.2951 |
49.1803 |
1.63934 |
| 9.0226 |
67.6692 |
15.7895 |
7.51880 |
The MEANS Procedure
|
|
|
| 22.1319800 |
| 46.1133697 |
| 26.2540671 |
| 5.5005832 |
|
| 10.2301014 |
| 23.7391251 |
| 18.0547195 |
| 3.6989117 |
|
| 9.0225564 |
| 12.2950820 |
| 7.8947368 |
| 1.3157895 |
|
| 36.8852459 |
| 67.6691729 |
| 49.1803279 |
| 8.6956522 |
|
| 5.00000 |
0.33333 |
0.66667 |
-1.00000 |
2.16667 |
0.00000 |
-2.16667 |
-0.83333 |
0.50000 |
0.33333 |
0.33333 |
-0.33333 |
| 4.94444 |
1.22222 |
-0.94444 |
-0.27778 |
2.88889 |
-0.27778 |
-2.61111 |
-0.27778 |
0.38889 |
-0.11111 |
0.05556 |
-0.05556 |
| 4.94444 |
0.05556 |
0.55556 |
-0.61111 |
1.05556 |
-0.11111 |
-0.94444 |
-1.44444 |
1.22222 |
0.22222 |
0.27778 |
-0.27778 |
| 5.05556 |
0.61111 |
-1.55556 |
0.94444 |
0.27778 |
0.27778 |
-0.55556 |
-1.55556 |
1.77778 |
-0.22222 |
0.05556 |
-0.05556 |
| 4.94444 |
0.22222 |
0.22222 |
-0.44444 |
2.55556 |
-0.11111 |
-2.44444 |
-0.61111 |
0.55556 |
0.05556 |
0.27778 |
-0.27778 |
Based on the importance values, price is the most important attribute for some of the respondents, but expected tread life
is most important for others. On the average, price is most important, followed by expected tread life and brand. Road hazard
insurance is less important. Each of the brands is preferred by some of the respondents. All respondents preferred a lower
price over a higher price, a longer tread life, and road hazard insurance.


 Model Statement UsageBox-Cox TransformationsUsing Splines and KnotsScoring Spline VariablesLinear and Nonlinear Regression FunctionsSimultaneously Fitting Two Regression FunctionsPenalized B-SplinesSmoothing SplinesSmoothing Splines Changes and EnhancementsIteration History Changes and EnhancementsANOVA CodingsMissing ValuesMissing Values, UNTIE, and Hypothesis TestsControlling the Number of IterationsUsing the REITERATE Algorithm OptionAvoiding Constant TransformationsConstant VariablesCharacter OPSCORE VariablesConvergence and DegeneraciesImplicit and Explicit InterceptsPassive ObservationsPoint ModelsRedundancy AnalysisOptimal ScalingOPSCORE, MONOTONE, UNTIE, and LINEAR TransformationsSPLINE and MSPLINE TransformationsSpecifying the Number of KnotsSPLINE, BSPLINE, and PSPLINE ComparisonsHypothesis TestsOutput Data SetOUTTEST= Output Data SetComputational ResourcesUnbalanced ANOVA without CLASS VariablesHypothesis Tests for Simple Univariate ModelsHypothesis Tests with Monotonicity ConstraintsHypothesis Tests with Dependent Variable TransformationsHypothesis Tests with One-Way ANOVAUsing the DESIGN Output OptionDiscrete Choice Experiments: DESIGN, NORESTORE, NOZEROCenteringDisplayed OutputODS Table NamesODS Graphics
Model Statement UsageBox-Cox TransformationsUsing Splines and KnotsScoring Spline VariablesLinear and Nonlinear Regression FunctionsSimultaneously Fitting Two Regression FunctionsPenalized B-SplinesSmoothing SplinesSmoothing Splines Changes and EnhancementsIteration History Changes and EnhancementsANOVA CodingsMissing ValuesMissing Values, UNTIE, and Hypothesis TestsControlling the Number of IterationsUsing the REITERATE Algorithm OptionAvoiding Constant TransformationsConstant VariablesCharacter OPSCORE VariablesConvergence and DegeneraciesImplicit and Explicit InterceptsPassive ObservationsPoint ModelsRedundancy AnalysisOptimal ScalingOPSCORE, MONOTONE, UNTIE, and LINEAR TransformationsSPLINE and MSPLINE TransformationsSpecifying the Number of KnotsSPLINE, BSPLINE, and PSPLINE ComparisonsHypothesis TestsOutput Data SetOUTTEST= Output Data SetComputational ResourcesUnbalanced ANOVA without CLASS VariablesHypothesis Tests for Simple Univariate ModelsHypothesis Tests with Monotonicity ConstraintsHypothesis Tests with Dependent Variable TransformationsHypothesis Tests with One-Way ANOVAUsing the DESIGN Output OptionDiscrete Choice Experiments: DESIGN, NORESTORE, NOZEROCenteringDisplayed OutputODS Table NamesODS Graphics
![]() ) data set into an (
) data set into an (![]() ) data set that can be merged with the factor level data set
) data set that can be merged with the factor level data set