Survivor Function Estimators :: SAS/STAT(R) 12.3 User's Guide

Breslow Estimator

To select this estimator, specify the METHOD=BRESLOW option in the BASELINE statement or OUTPUT statement. For the jth subject, let $\{ (X_ j, \Delta _ j, \bZ _ j(.))\}$ represent the failure time, the event indicator, and the vector of covariate values, respectively. For $t \geq 0$ , let

$\displaystyle Y_ j(t)$	$\displaystyle =$	$\displaystyle I(X_ j \geq t)$
$\displaystyle \Delta _ j(t)$	$\displaystyle =$	$\displaystyle \left\{ \begin{array}{ll} 1 & X_ j=t ~ \& ~ \Delta _ j=1\\ 0 & \textrm{otherwise} \end{array} \right.$
$\displaystyle d(t)$	$\displaystyle =$	$\displaystyle \sum _ j\Delta _ j(t)$

Note that is the number of subjects that have an event at t. Let

$\displaystyle S^{(0)}(\bbeta ,t)$	$\displaystyle =$	$\displaystyle \sum _{j} Y_{j}(t) \mr {e}^{\bbeta \bZ _{j}(t)}$
$\displaystyle S^{(1)}(\bbeta ,t)$	$\displaystyle =$	$\displaystyle \sum _{j} Y_{j}(t) \mr {e}^{\bbeta \bZ _{j}(t)} \bZ _{j}(t)$
$\displaystyle \bar{\bZ }(\bbeta ,t)$	$\displaystyle =$	$\displaystyle \frac{ S^{(1)}(\bbeta ,t)}{ S^{(0)}(\bbeta ,t)}$

For a given realization of the explanatory variables $\bxi$ , the cumulative hazard function estimator at $\bxi$ is

$\hat{\Lambda }_ B(t,\bxi ) = \mr {e}^{\hat{\bbeta }\bxi } \sum _{t_ i\leq t} \frac{d(t_ i)}{S^{(0)}(\hat{\bbeta },t_ i)}$

with variance estimated by

$\hat{\sigma }^2(\hat{\Lambda }_ B(t,\bxi )) = \mr {e}^{2\hat{\bbeta }\bxi } \sum _{t_ i \leq t} \frac{d(t_ i)}{[S^{(0)}(\hat{\bbeta },t_ i)]^2} + H(t,\bxi )’[\mc {I}(\hat{\bbeta })]^{-1} H(t,\bxi )$

where

$H(t,\bxi ) = \mr {e}^{\hat{\bbeta }\bxi }\sum _{t_ i \leq t} \frac{d(t_ i)}{S^{(0)}(\hat{\bbeta },t_ i)} \biggl ( \bar{\bZ }(\hat{\bbeta },t_ i)- \bxi \biggr )$

For the marginal model, the variance estimator computation follows Spiekerman and Lin (1998).

The Breslow estimate of the survivor function for $\bZ =\bxi$ is

$\hat{S}_ B(t,\bxi ) = \exp (-\hat{\Lambda }_ B(t,\bxi ))$

By the delta method, the standard error of $\hat{S}_ B(t,\bxi )$ is approximated by

$\hat{\sigma }(\hat{S}_ B(t,\bxi )) = \hat{S}_ B(t,\bxi ) \hat{\sigma }(\hat{\Lambda }_ B(t,\bxi ))$

Fleming-Harrington Estimator

To select this estimator, specify the METHOD=FH option in the BASELINE statement or OUTPUT statement. With and as defined in the section Breslow Estimator and for $1\leq k \leq d(t)$ , let

$\displaystyle S_ E^{(0)}(\bbeta ,k, t)$	$\displaystyle =$	$\displaystyle \sum _{j} Y_{j}(t) \biggl \{ 1- \frac{k-1}{d(t)} \Delta _{j}(t) \biggr \} \mr {e}^{\bbeta \bZ _{j}(t)}$
$\displaystyle S_ E^{(1)}(\bbeta ,k,t)$	$\displaystyle =$	$\displaystyle \sum _{j} Y_{j}(t) \biggl \{ 1- \frac{k-1}{d(t)} \Delta _{j}(t) \biggr \} \mr {e}^{\bbeta \bZ _{j}(t)} \bZ _{j}(t)$
$\displaystyle \bar{\bZ }_ E\bbeta ,k,t)$	$\displaystyle =$	$\displaystyle \frac{ S_ E^{(1)}(\bbeta ,k,t)}{ S_ E^{(0)}(\bbeta ,k,t) }$

For a given realization of the explanatory variables, the Fleming-Harrington adjustment of the cumulative hazard function is

$\hat{\Lambda }_ F(t,\bxi ) = \mr {e}^{\hat{\bbeta }\bxi } \sum _{t_ i\leq t} \biggr \{ \sum _{k=1}^{d(t_ i)} \frac{1}{S_ E^{(0)}(\hat{\bbeta },k,t_ i)} \biggr \}$

with variance estimated by

$\hat{\sigma }^2(\hat{\Lambda }_ F(t,\bxi )) = \mr {e}^{2\hat{\bbeta }\bxi } \sum _{t_ i \leq t} \biggl \{ \sum _{k=1}^{d(t_ i)} \frac{1}{[S_ E^{(0)}(\hat{\bbeta },k,t_ i)]^2} \biggr \} + H_ E(t,\bxi )’[\mc {I}(\hat{\bbeta })]^{-1} H_ E(t,\bxi )$

where

$H_ E(t,\bxi ) = \mr {e}^{\hat{\bbeta }\bxi } \biggl \{ \biggl [\sum _{t_ i \leq t} \sum _{k=1}^{d(t_ i)} \frac{1}{ S_ E^{(0)}(\hat{\bbeta },k,t_ i)} \bar{\bZ }_ E(\hat{\bbeta },k, t_ i) \biggr ] - \hat{\Lambda }_ F(t,\mb {0})\bxi \biggl \}$

The Fleming-Harrington estimate of the survivor function for $\bZ =\bxi$ is

$\hat{S}_ F(t,\bxi ) = \exp (-\hat{\Lambda }_ F(t,\bxi ))$

By the delta method, the standard error of $\hat{S}_ B(t,\bxi )$ is approximated by

$\hat{\sigma }(\hat{S}_ F(t,\bxi )) = \hat{S}_ F(t,\bxi ) \hat{\sigma }(\hat{\Lambda }_ F(t,\bxi ))$

Product-Limit Estimator

To select this estimator, specify the METHOD=PL option in the BASELINE statement or OUTPUT statement. Let $\mc {D}_ i$ denote the set of individuals that fail at . Let $\mc {C}_ i$ denote the set of individuals that are censored in the half-open interval $[t_{i} , t_{i+1})$ , where $t_{0}=0$ and $t_{k+1}=\infty$ . Let $\gamma _ l$ denote the censoring times in $[t_{i} , t_{i+1})$ , where l ranges over $\mc {C}_ i$ .

The likelihood function for all individuals is given by

$\mc {L}=\prod _{i=0}^{k} \left\{ \prod _{l \in \mc {D}_ i} \left( [S_{0}(t_{i})]^{ \ \mr {exp}(\mb {Z}_{l}\bbeta ) } -[S_{0}(t_{i}+0)]^{ \ \mr {exp}(\mb {Z}_{l}\bbeta ) } \right) \prod _{l \in \mc {C}_ i} [S_{0}(\gamma _{l}+0)]^{\ \mr {exp}(\mb {Z}_{l}\bbeta )} \right\}$

where $\mc {D}_0$ is empty. The likelihood $\mc {L}$ is maximized by taking $S_{0}(t)=S_{0}(t_{i}+0)$ for $t_{i}<t \leq t_{i+1}$ and allowing the probability mass to fall only on the observed event times $t_{1}$ , $\ldots \$ , $t_{k}$ . By considering a discrete model with hazard contribution $1-\alpha _{i}$ at , you take $S_{0}(t_{i})=S_{0}(t_{i-1}+0)=\prod _{j=0}^{i-1} \alpha _ j$ , where $\alpha _{0}=1$ . Substitution into the likelihood function produces

$\mc {L}=\prod _{i=0}^{k} \left\{ \prod _{j \in \mc {D}_ i } \left( 1-\alpha _{i}^{\ \mr {exp}(\mb {Z}_{j}\bbeta ) } \right) \prod _{ l \in \mc {R}_{i}-\mc {D}_{i} } \alpha _{i}^{ \ \mr {exp}(\mb {z}_{l}\bbeta )} \right\}$

If you replace $\bbeta$ with $\hat{\bbeta }$ estimated from the partial likelihood function and then maximize with respect to $\alpha _{1},\ldots , \alpha _{k}$ , the maximum likelihood estimate $\hat{\alpha }_ i$ of $\alpha _ i$ becomes a solution of

$\sum _{ j \in \mc {D}_ i } \frac{ \mr {exp}(\mb {Z}_{j}\hat{\bbeta }) }{ 1-\hat{\alpha }_{i}^{ \ \mr {exp}(\mb {Z}_{j}\hat{\bbeta }) } } =\sum _{l \in \mc {R}_ i } \mr {exp}(\mb {Z}’_{l}\hat{\bbeta })$

When only a single failure occurs at $t_{i}$ , $\hat{\alpha }_{i}$ can be found explicitly. Otherwise, an iterative solution is obtained by the Newton method.

The baseline survival function is estimated by

$\hat{S}_{0}(t)=\hat{S}_{0}(t_{i-1}+0) =\prod _{j=0}^{i-1} \hat{\alpha }_{j}, t_{i-1} < t \leq t_{i}$

For a given realization of the explanatory variables $\bxi$ , the product-limit estimate of the survival function at $\bZ =\bxi$ is

$\hat{S}_ P(t,\bxi ) = [\hat{S}_{0}(t)]^{\mr {exp}(\bbeta \bxi )}$

Approximating the variance of $-\log (S_ P(t,\bxi ))$ by the variance estimate of the Breslow estimator of the cumulative hazard function, the variance of the product-limit estimator at $\bZ =\bxi$ is given by

$\hat{\sigma }(\hat{S}_ P(t,\bxi )) = \hat{S}_ P(t,\bxi ) \hat{\sigma }(\hat{\Lambda }_ B(t,\bxi ))$

Direct Adjusted Survival Curves

Consider the Breslow estimator of the survival function. For $j=1,\ldots ,n$ , let $\bxi _ j$ represent the covariate set of the jth patient. The direct adjusted survival curve averages the estimated survival curves for each patient:

$\bar{S}(t) = \frac{1}{n}\sum _{j=1}^ n \hat{S}(t,\bxi _ j)$

The variance of $\bar{S}(t)$ can be estimated by

$\hat{\sigma }^2(\bar{S}(t)) = \frac{1}{n^2} \biggl (V^{(1)}t)+V^{(2)}(t) \biggr )$

where

$\displaystyle V^{(1)}(t)$	$\displaystyle =$	$\displaystyle \biggl ( \sum _{j=1}^ n \mr {e}^{\hat{\bbeta }\bxi _ j} \hat{S}(t,\bxi _ j) \biggr )^2 \sum _{t_ i\leq t} \frac{d(t_ i)}{[S^{(0)}(\hat{\bbeta },t_ i)]^2}$
$\displaystyle V^{(2)}(t)$	$\displaystyle =$	$\displaystyle \biggl (\sum _{j=1}^ n \hat{S}(t,\bxi _ j)H(t,\bxi _ j)\biggr )’ \biggl [\mc {I}(\hat{\bbeta }) \biggr ]^{-1} \biggl (\sum _{j=1}^ n \hat{S}(t,\bxi _ j) H(t,\bxi _ j) \biggr )$

Comparison of Direct Adjusted Probabilities of Two Strata

For a stratified Cox model, let k index the strata. For the jth patient, let $\hat{S}_ k(t,\bxi _ j)$ and $H_ k(t, \bxi _ j)$ be the estimated survival function and the $\bH$ vector for the kth stratum. The direct adjusted survival curve for the kth stratum is

$\bar{S}_ k(t) = \frac{1}{n}\sum _{j=1}^ n \hat{S}_ k(t,\bxi _{j})$

The variance of $\bar{S}_1(t) - \bar{S}_2(t)$ can be estimated by

$\hat{\sigma }^2(\bar{S}_1(t) - \bar{S}_2(t)) = \frac{1}{n^2} \biggl (U^{(1)}_1(t)+U^{(1)}_2 + U^{(2)}_{12}(t) \biggr )$

where

$\displaystyle U^{(1)}_ k(t)$	$\displaystyle =$	$\displaystyle \left( \sum _{j=1}^ n \mr {e}^{\bbeta \bxi _{j}} \hat{S}_ k(t,\bxi _{j}) \right)^2 \sum _{t_ i\leq t} \frac{d(t_ i)}{[S^{(0)}(\hat{\bbeta },t_ i)]^2} \mbox{~ ~ ~ } k=1,2$
$\displaystyle U^{(2)}_{12}(t)$	$\displaystyle =$	$\displaystyle \left\{ \sum _{j=1}^ n \left[\hat{S}_1(t,\bxi _{j})H_1(t,\bxi _{j})-\hat{S}_2(t,\bxi _{j})H_2(t,\bxi _{j}) \right] \right\} ^{\prime } \mc {I} ^{-1}(\hat{\bbeta })$
$\displaystyle$	$\displaystyle$	$\displaystyle \left\{ \sum _{j=1}^ n \left[\hat{S}_1(t,\bxi _{j})H_2(t,\bxi _{j})-\hat{S}_1(t,\bxi _{j})H(_2t,\bxi _{j}) \right] \right\}$

Comparison of Direct Adjusted Survival Probabilities of Two Treatments

For $j=1,\ldots ,n$ , let $\bxi _{jk}$ represent the covariate set of the jth patient with the kth treatment, . The direct adjusted survival curve for the kth treatment is

$\bar{S}_ k(t) = \frac{1}{n}\sum _{i=j}^ n \hat{S}(t,\bxi _{jk})$

The variance of $\bar{S}_1(t) - \bar{S}_2(t)$ can be estimated by

$\hat{\sigma }^2\left(\bar{S}_1(t)-\bar{S}_2(t)\right) = \frac{1}{n^2} \biggl (V^{(1)}_{12}(t) + V^{(2)}_{12}(t) \biggr )$

where

$\displaystyle V^{(1)}_{12}(t)$	$\displaystyle =$	$\displaystyle \left\{ \sum _{j=1}^ n \left[\mr {e}^{\bbeta \bxi _{1j}} \hat{S}(t,\bxi _{1j}) - \mr {e}^{\bbeta \bxi _{2j}} \hat{S}(t,\bxi _{2j}) \right] \right\} ^2 \sum _{t_ i\leq t} \frac{d(t_ i)}{[S^{(0)}(\hat{\bbeta },t_ i)]^2}$
$\displaystyle V^{(2)}_{12}(t)$	$\displaystyle =$	$\displaystyle \left\{ \sum _{j=1}^ n \left[\hat{S}(t,\bxi _{1j})H(t,\bxi _{1j})-\hat{S}(t,\bxi _{2j})H(t,\bxi _{2j}) \right] \right\} ^{\prime } \mc {I} ^{-1}(\hat{\bbeta })$
$\displaystyle$	$\displaystyle$	$\displaystyle \left\{ \sum _{j=1}^ n \left[\hat{S}(t,\bxi _{1j})H(t,\bxi _{1j})-\hat{S}(t,\bxi _{2j})H(t,\bxi _{2j}) \right] \right\}$

Confidence Intervals for the Survivor Function

When the computation of confidence limits for the survivor function is based on the asymptotic normality of the survival estimator $\hat{S}(t)$ —which can be the Breslow estimator $\hat{S}_ B(t)$ , the Fleming-Harrington estimator $\hat{S}_ F(t)$ , or the product-limit estimator $\hat{S}_ P(t)$ —the approximate confidence interval might include impossible values outside the range [0,1] at extreme values of t. This problem can be avoided by applying the asymptotic normality to a transformation of for which the range is unrestricted. In addition, certain transformed confidence intervals for perform better than the usual linear confidence intervals (Borgan and Liestøl, 1990). The CLTYPE= option in the BASELINE statement enables you to choose one of the following transformations: the log-log function, the log function, and the linear function.

Let g be the transformation that is being applied to the survivor function . By the delta method, the standard error of $g(\hat{S}(t))$ is estimated by

$\tau (t) = \hat{\sigma }\left[g(\hat{S}(t))\right] = g’\left(\hat{S}(t)\right)\hat{\sigma }[\hat{S}(t)]$

where is the first derivative of the function g. The 100(1– $\alpha$ )% confidence interval for is given by

$g^{-1}\left\{ g[\hat{S}(t)] \pm z_{\frac{\alpha }{2}} g’[\hat{S}(t)]\hat{\sigma }[\hat{S}(t)] \right\}$

where $g^{-1}$ is the inverse function of g. The choices for the transformation g are as follows:

CLTYPE=NORMAL specifies linear transformation, which is the same as having no transformation in which g is the identity. The 100(1– $\alpha$ )% confidence interval for 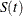is given by

$\hat{S}(t) - z_{\frac{\alpha }{2}}\hat{\sigma }\left[\hat{S}(t)\right] \le S(t) \le \hat{S}(t) + z_{\frac{\alpha }{2}}\hat{\sigma }\left[\hat{S}(t)\right]$
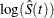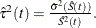CLTYPE=LOG specifies log transformation. The estimated variance of $\log (\hat{S}(t))$ is $\hat{\tau }^2(t) = \frac{\hat{\sigma }^2(\hat{S}(t))}{\hat{S}^2(t)}.$ The 100(1– $\alpha$ )% confidence interval for 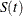is given by

$\hat{S}(t)\exp \left(-z_{\frac{\alpha }{2}}\hat{\tau }(t)\right) \le S(t) \le \hat{S}(t)\exp \left(z_{\frac{\alpha }{2}}\hat{\tau }(t)\right)$
CLTYPE=LOGLOG specifies log-log transformation. The estimated variance of 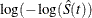$\log (-\log (\hat{S}(t))$ is $\hat{\tau }^2(t) = \frac{\hat{\sigma }^2[\hat{S}(t)]}{ [\hat{S}(t)\log (\hat{S}(t))]^2 }.$ The 100(1– $\alpha$ )% confidence interval for 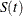is given by

$\left[\hat{S}(t)\right]^{\exp \left( z_{\frac{\alpha }{2}} \hat{\tau }(t)\right)} \le S(t) \le \left[\hat{S}(t)\right]^{\exp \left(-z_{\frac{\alpha }{2}} \hat{\tau }(t)\right)}$

The PHREG Procedure