The GLM Procedure

Afifi, A. A. and Azen, S. P. (1972), Statistical Analysis: A Computer-Oriented Approach, New York: Academic Press.

Anderson, T. W. (1958), An Introduction to Multivariate Statistical Analysis, New York: John Wiley & Sons.

Bartlett, M. S. (1937), “Properties of Sufficiency and Statistical Tests,” Proceedings of the Royal Society of London, Series A, 160, 268–282.

Begun, J. M. and Gabriel, K. R. (1981), “Closure of the Newman-Keuls Multiple Comparisons Procedure,” Journal of the American Statistical Association, 76, 374.

Belsley, D. A., Kuh, E., and Welsch, R. E. (1980), Regression Diagnostics: Identifying Influential Data and Sources of Collinearity, New York: John Wiley & Sons.

Bishop, Y. M. M., Fienberg, S. E., and Holland, P. W. (1975), Discrete Multivariate Analysis: Theory and Practice, Cambridge, MA: MIT Press.

Box, G. E. P. (1953), “Non-normality and Tests on Variances,” Biometrika, 40, 318–335.

Box, G. E. P. (1954), “Some Theorems on Quadratic Forms Applied in the Study of Analysis of Variance Problems, Part 2: Effects of Inequality of Variance and of Correlation between Errors in the Two-Way Classification,” Annals of Mathematical Statistics, 25, 484–498.

Brown, M. B. and Forsythe, A. B. (1974), “Robust Tests for Equality of Variances,” Journal of the American Statistical Association, 69, 364–367.

Carmer, S. G. and Swanson, M. R. (1973), “Evaluation of Ten Pairwise Multiple Comparison Procedures by Monte Carlo Methods,” Journal of the American Statistical Association, 68, 66–74.

Chi, Y.-Y., Gribbin, M. J., Lamers, Y., Gregory, J. F., III, and Muller, K. E. (2012), “Global Hypothesis Testing for High-Dimensional Repeated Measures Outcomes,” Statistics in Medicine, 31, 724–742.

Cochran, W. G. and Cox, G. M. (1957), Experimental Designs, 2nd Edition, New York: John Wiley & Sons.

Cohen, J. (1988), Statistical Power Analysis for the Behavioral Sciences, Hillsdale, NJ: Lawrence Erlbaum Associates.

Cohen, R. (2002), “SAS Meets Big Iron: High Performance Computing in SAS Analytical Procedures,” in Proceedings of the Twenty-Seventh Annual SAS Users Group International Conference, Cary, NC: SAS Institute Inc.

Cole, J. W. L. and Grizzle, J. E. (1966), “Applications of Multivariate Analysis of Variance to Repeated Measures Experiments,” Biometrics, 22, 810–828.

Conover, W. J., Johnson, M. E., and Johnson, M. M. (1981), “A Comparative Study of Tests for Homogeneity of Variances, with Applications to the Outer Continental Shelf Bidding Data,” Technometrics, 23, 351–361.

Cornfield, J. and Tukey, J. W. (1956), “Average Values of Mean Squares in Factorials,” Annals of Mathematical Statistics, 27, 907–949.

Draper, N. R. and Smith, H. (1966), Applied Regression Analysis, New York: John Wiley & Sons.

Duncan, D. B. (1975), “t Tests and Intervals for Comparisons Suggested by the Data,” Biometrics, 31, 339–359.

Dunnett, C. W. (1955), “A Multiple Comparisons Procedure for Comparing Several Treatments with a Control,” Journal of the American Statistical Association, 50, 1096–1121.

Dunnett, C. W. (1980), “Pairwise Multiple Comparisons in the Homogeneous Variance, Unequal Sample Size Case,” Journal of the American Statistical Association, 75, 789–795.

Edwards, D. and Berry, J. J. (1987), “The Efficiency of Simulation-Based Multiple Comparisons,” Biometrics, 43, 913–928.

Einot, I. and Gabriel, K. R. (1975), “A Study of the Powers of Several Methods of Multiple Comparisons,” Journal of the American Statistical Association, 70, 351.

Fidler, F. and Thompson, B. (2001), “Computing Correct Confidence Intervals for ANOVA Fixed- and Random-Effects Effect Sizes,” Educational and Psychological Measurement, 61, 575–604.

Freund, R. J., Littell, R. C., and Spector, P. C. (1986), SAS System for Linear Models, 1986 Edition, Cary, NC: SAS Institute Inc.

Gabriel, K. R. (1978), “A Simple Method of Multiple Comparisons of Means,” Journal of the American Statistical Association, 73, 364.

Games, P. A. (1977), “An Improved t Table for Simultaneous Control on g Contrasts,” Journal of the American Statistical Association, 72, 531–534.

Goodnight, J. H. (1976), “The New General Linear Models Procedure,” in Proceedings of the First Annual SAS Users Group International Conference, Cary, NC: SAS Institute Inc.

Goodnight, J. H. (1978a), The SWEEP Operator: Its Importance in Statistical Computing, Technical Report R-106, SAS Institute Inc., Cary, NC.

Goodnight, J. H. (1978b), Tests of Hypotheses in Fixed-Effects Linear Models, Technical Report R-101, SAS Institute Inc., Cary, NC.

Goodnight, J. H. (1979), “A Tutorial on the Sweep Operator,” American Statistician, 33, 149–158.

Goodnight, J. H. and Harvey, W. R. (1978), Least-Squares Means in the Fixed-Effects General Linear Models, Technical Report R-103, SAS Institute Inc., Cary, NC.

Goodnight, J. H. and Speed, F. M. (1978), Computing Expected Mean Squares, Technical Report R-102, SAS Institute Inc., Cary, NC.

Graybill, F. A. (1961), An Introduction to Linear Statistical Models, volume 1, New York: McGraw-Hill.

Greenhouse, S. W. and Geisser, S. (1959), “On Methods in the Analysis of Profile Data,” Psychometrika, 32, 95–112.

Gribbin, M. J. (2007), Better Power Methods for the Univariate Approach to Repeated Measures, Ph.D. diss., University of North Carolina, Department of Biostatistics.

Guirguis, G. H. and Tobias, R. D. (2004), “On the Computation of the Distribution for the Analysis of Means,” Communications in Statistics—Simulation and Computation, 33, 861–888.

Hand, D. J., Daly, F., Lunn, A. D., McConway, K. J., and Ostrowski, E. (1994), A Handbook of Small Data Sets, London: Chapman & Hall.

Hartley, H. O. and Searle, S. R. (1969), “On Interaction Variance Components in Mixed Models,” Biometrics, 25, 573–576.

Harvey, W. R. (1975), Least-Squares Analysis of Data with Unequal Subclass Numbers, Technical Report ARS H-4, U.S. Department of Agriculture, Agriculture Research Service.

Hayter, A. J. (1984), “A Proof of the Conjecture That the Tukey-Kramer Method Is Conservative,” Annals of Statistics, 12, 61–75.

Hayter, A. J. (1989), “Pairwise Comparisons of Generally Correlated Means,” Journal of the American Statistical Association, 84, 208–213.

Heck, D. L. (1960), “Charts of Some Upper Percentage Points of the Distribution of the Largest Characteristic Root,” Annals of Mathematical Statistics, 31, 625–642.

Hochberg, Y. (1974), “Some Conservative Generalizations of the T-Method in Simultaneous Inference,” Journal of Multivariate Analysis, 4, 224–234.

Hocking, R. R. (1973), “A Discussion of the Two-Way Mixed Model,” American Statistician, 27, 148–152.

Hocking, R. R. (1976), “The Analysis and Selection of Variables in a Linear Regression,” Biometrics, 32, 1–50.

Hocking, R. R. (1985), The Analysis of Linear Models, Monterey, CA: Brooks/Cole.

Hsu, J. C. (1992), “The Factor Analytic Approach to Simultaneous Inference in the General Linear Model,” Journal of Computational and Graphical Statistics, 1, 151–168.

Hsu, J. C. (1996), Multiple Comparisons: Theory and Methods, London: Chapman & Hall.

Hsu, J. C. and Nelson, B. L. (1998), “Multiple Comparisons in the General Linear Model,” Journal of Computational and Graphical Statistics, 7, 23–41.

Huynh, H. and Feldt, L. S. (1970), “Conditions Under Which Mean Square Ratios in Repeated Measurements Designs Have Exact F-Distributions,” Journal of the American Statistical Association, 65, 1582–1589.

Huynh, H. and Feldt, L. S. (1976), “Estimation of the Box Correction for Degrees of Freedom from Sample Data in the Randomized Block and Split Plot Designs,” Journal of Educational Statistics, 1, 69–82.

Johnson, N. L., Kotz, S., and Balakrishnan, N. (1994), Continuous Univariate Distributions, volume 1, 2nd Edition, New York: John Wiley & Sons.

Kennedy, W. J., Jr. and Gentle, J. E. (1980), Statistical Computing, New York: Marcel Dekker.

Kramer, C. Y. (1956), “Extension of Multiple Range Tests to Group Means with Unequal Numbers of Replications,” Biometrics, 12, 307–310.

Krishnaiah, P. R. and Armitage, J. V. (1966), “Tables for Multivariate t Distribution,” Sankhy, Series B, 28, 31–56.

Kutner, M. H. (1974), “Hypothesis Testing in Linear Models (Eisenhart Model),” American Statistician, 28, 98–100.

LaTour, S. A. and Miniard, P. W. (1983), “The Misuse of Repeated Measures Analysis in Marketing Research,” Journal of Marketing Research, 20, 45–57.

Lecoutre, B. (1991), “A Correction for the Epsilon Approximate Test with Repeated Measures Design with Two or More Independent Groups,” Journal of Educational Statistics, 16, 371–372.

Levene, H. (1960), “Robust Tests for the Equality of Variance,” in I. Olkin, ed., Contributions to Probability and Statistics, 278–292, Palo Alto, CA: Stanford University Press.

Marcus, R., Peritz, E., and Gabriel, K. R. (1976), “On Closed Testing Procedures with Special Reference to Ordered Analysis of Variance,” Biometrika, 63, 655–660.

Maxwell, S. E. (2000), “Sample Size and Multiple Regression Analysis,” Psychological Methods, 5, 434–458.

McLean, R. A., Sanders, W. L., and Stroup, W. W. (1991), “A Unified Approach to Mixed Linear Models,” American Statistician, 45, 54–64.

Miller, R. G., Jr. (1981), Simultaneous Statistical Inference, New York: Springer-Verlag.

Milliken, G. A. and Johnson, D. E. (1984), Designed Experiments, Analysis of Messy Data, Belmont, CA: Lifetime Learning Publications.

Morrison, D. F. (1976), Multivariate Statistical Methods, 2nd Edition, New York: McGraw-Hill.

Nelder, J. A. (1994), “The Statistics of Linear Models: Back to Basics,” Statistics and Computing, 4, 221–234.

Nelson, P. R. (1982), “Exact Critical Points for the Analysis of Means,” Communications in Statistics—Theory and Methods, 11, 699–709.

Nelson, P. R. (1991), “Numerical Evaluation of Multivariate Normal Integrals with Correlations 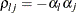,” in A. Öztürk and E. C. van der Meulen, eds., Frontiers of Statistical Scientific Theory and Industrial Applications: Proceedings of the ICOSCO I Conference, 97–114, Columbus, OH: American Sciences Press.

Nelson, P. R. (1993), “Additional Uses for the Analysis of Means and Extended Tables of Critical Values,” Technometrics, 35, 61–71.

O’Brien, R. G. (1979), “A General ANOVA Method for Robust Tests of Additive Models for Variances,” Journal of the American Statistical Association, 74, 877–880.

O’Brien, R. G. (1981), “A Simple Test for Variance Effects in Experimental Designs,” Psychological Bulletin, 89, 570–574.

O’Brien, R. G. and Heft, M. W. (1995), “New Discrimination Indexes and Models for Studying Sensory Functioning in Aging,” Journal of Applied Statistics, 22, 9–27.

Olejnik, S. F. and Algina, J. (1987), “Type I Error Rates and Power Estimates of Selected Parametric and Non-parametric Tests of Scale,” Journal of Educational Statistics, 12, 45–61.

Ott, E. R. (1967), “Analysis of Means: A Graphical Procedure,” Industrial Quality Control, 24, 101–109, reprinted in Journal of Quality Technology, 15 (1983), 10–18.

Perlman, M. D. and Rasmussen, U. A. (1975), “Some Remarks on Estimating a Noncentrality Parameter,” Communications in Statistics—Theory and Methods, 4, 455–468.

Petrinovich, L. F. and Hardyck, C. D. (1969), “Error Rates for Multiple Comparison Methods: Some Evidence Concerning the Frequency of Erroneous Conclusions,” Psychological Bulletin, 71, 43–54.

Pillai, K. C. S. (1960), Statistical Table for Tests of Multivariate Hypotheses, Manila: Statistical Center, University of Philippines.

Pringle, R. M. and Rayner, A. A. (1971), Generalized Inverse Matrices with Applications to Statistics, New York: Hafner Publishing.

Ramsey, P. H. (1978), “Power Differences between Pairwise Multiple Comparisons,” Journal of the American Statistical Association, 73, 479–485.

Rao, C. R. (1965), Linear Statistical Inference and Its Applications, New York: John Wiley & Sons.

Rodriguez, R. N., Tobias, R. D., and Wolfinger, R. D. (1995), “Comments on J. A. Nelder, 'The Statistics of Linear Models: Back to Basics',” Statistics and Computing, 5, 97–101.

Ryan, T. A. (1959), “Multiple Comparisons in Psychological Research,” Psychological Bulletin, 56, 26–47.

Ryan, T. A. (1960), “Significance Tests for Multiple Comparison of Proportions, Variances, and Other Statistics,” Psychological Bulletin, 57, 318–328.

Satterthwaite, F. E. (1946), “An Approximate Distribution of Estimates of Variance Components,” Biometrics Bulletin, 2, 110–114.

Schatzoff, M. (1966), “Exact Distributions of Wilks’s Likelihood Ratio Criterion,” Biometrika, 53, 347–358.

Scheffé, H. (1953), “A Method for Judging All Contrasts in the Analysis of Variance,” Biometrika, 40, 87–104.

Scheffé, H. (1959), The Analysis of Variance, New York: John Wiley & Sons.

Searle, S. R. (1971), Linear Models, New York: John Wiley & Sons.

Searle, S. R. (1987), Linear Models for Unbalanced Data, New York: John Wiley & Sons.

Searle, S. R. (1995), “Comments on J. A. Nelder, 'The Statistics of Linear Models: Back to Basics',” Statistics and Computing, 5, 103–107.

Searle, S. R., Casella, G., and McCulloch, C. E. (1992), Variance Components, New York: John Wiley & Sons.

Searle, S. R., Speed, F. M., and Milliken, G. A. (1980), “Population Marginal Means in the Linear Model: An Alternative to Least Squares Means,” American Statistician, 34, 216–221.

Šidák, Z. (1967), “Rectangular Confidence Regions for the Means of Multivariate Normal Distributions,” Journal of the American Statistical Association, 62, 626–633.

Smithson, M. (2003), Confidence Intervals, Thousand Oaks, CA: Sage Publications.

Smithson, M. (2004), personal communication.

Snedecor, G. W. and Cochran, W. G. (1967), Statistical Methods, 6th Edition, Ames: Iowa State University Press.

Steel, R. G. D. and Torrie, J. H. (1960), Principles and Procedures of Statistics, New York: McGraw-Hill.

Steiger, J. H. and Fouladi, R. T. (1997), “Noncentrality Interval Estimation and the Evaluation of Statistical Models,” in L. Harlow, S. Mulaik, and J. H. Steiger, eds., What If There Were No Significance Tests?, 222–257, Hillsdale, NJ: Lawrence Erlbaum Associates.

Stenstrom, F. H. (1940), The Growth of Snapdragons, Stocks, Cinerarias, and Carnations on Six Iowa Soils, Master’s thesis, Iowa State College.

Tubb, A., Parker, A. J., and Nickless, G. (1980), “The Analysis of Romano-British Pottery by Atomic Absorption Spectrophotometry,” Archaeometry, 22, 153–171.

Tukey, J. W. (1952), “Allowances for Various Types of Error Rates,” Invited address to Blacksburg meeting of Institute of Mathematical Studies.

Tukey, J. W. (1953), “The Problem of Multiple Comparisons,” in H. I. Braun, ed., Multiple Comparisons, 1948–1983, volume 8 of The Collected Works of John W. Tukey (published 1994), 1–300, London: Chapman & Hall, unpublished manuscript.

Urquhart, N. S. (1968), “Computation of Generalized Inverse Matrices Which Satisfy Specific Conditions,” SIAM Review, 10, 216–218.

Waller, R. A. and Duncan, D. B. (1969), “A Bayes Rule for the Symmetric Multiple Comparison Problem,” Journal of the American Statistical Association, 64, 1484–1499.

Waller, R. A. and Duncan, D. B. (1972), “Corrigenda to 'A Bayes Rule for the Symmetric Multiple Comparison Problem',” Journal of the American Statistical Association, 67, 253–255.

Waller, R. A. and Kemp, K. E. (1976), “Computations of Bayesian t-Values for Multiple Comparisons,” Journal of Statistical Computation and Simulation, 75, 169–172.

Welch, B. L. (1951), “On the Comparison of Several Mean Values: An Alternative Approach,” Biometrika, 38, 330–336.

Welsch, R. E. (1977), “Stepwise Multiple Comparison Procedures,” Journal of the American Statistical Association, 72, 359.

Westfall, P. H. and Young, S. S. (1993), Resampling-Based Multiple Testing: Examples and Methods for p-Value Adjustment, New York: John Wiley & Sons.

Winer, B. J. (1971), Statistical Principles in Experimental Design, 2nd Edition, New York: McGraw-Hill.

Wolfinger, R. D. and Chang, M. (1995), “Comparing the SAS GLM and MIXED Procedures for Repeated Measures,” in Proceedings of the Twentieth Annual SAS Users Group Conference, Cary, NC: SAS Institute Inc.

Yin, G. Z. and Jillie, D. W. (1987), “Orthogonal Design for Process Optimization and Its Application in Plasma Etching,” Solid State Technology, 30, 127–132.