The FASTCLUS Procedure
Unless the SHORT or SUMMARY option is specified, PROC FASTCLUS displays the following:
-
Initial Seeds, cluster seeds selected after one pass through the data
-
Change in Cluster Seeds for each iteration, if you specify MAXITER=n > 1
If you specify the LEAST=p option, with (1 < p < 2), and you omit the IRLS option, an additional column is displayed in the Iteration History table. This column contains a character to identify the method used in each iteration. PROC FASTCLUS chooses the most efficient method to cluster the data at each iterative step, given the condition of the data. Thus, the method chosen is data dependent. The possible values are described as follows:
|
Value |
Method |
|
|---|---|---|
|
N |
Newton’s Method |
|
|
I or L |
iteratively weighted least squares (IRLS) |
|
|
1 |
IRLS step, halved once |
|
|
2 |
IRLS step, halved twice |
|
|
3 |
IRLS step, halved three times |
PROC FASTCLUS displays a Cluster Summary, giving the following for each cluster:
-
Cluster number
-
Frequency, the number of observations in the cluster
-
Weight, the sum of the weights of the observations in the cluster, if you specify the WEIGHT statement
-
RMS Std Deviation, the root mean squared across variables of the cluster standard deviations, which is equal to the root mean square distance between observations in the cluster
-
Maximum Distance from Seed to Observation, the maximum distance from the cluster seed to any observation in the cluster
-
Nearest Cluster, the number of the cluster with mean closest to the mean of the current cluster
-
Centroid Distance, the distance between the centroids (means) of the current cluster and the nearest other cluster
A table of statistics for each variable is displayed unless you specify the SUMMARY option. The table contains the following:
-
Total STD, the total standard deviation
-
Within STD, the pooled within-cluster standard deviation
-
R-Square, the R square for predicting the variable from the cluster
-
RSQ/(1 - RSQ), the ratio of between-cluster variance to within-cluster variance
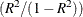
-
OVER-ALL, all of the previous quantities pooled across variables
PROC FASTCLUS also displays the following:
-
Pseudo F Statistic,
![\[ \frac{ \frac{R^2}{c - 1} }{ \frac{1 - R^2}{n - c} } \]](images/statug_fastclus0052.png)
where R square is the observed overall R square, c is the number of clusters, and n is the number of observations. The pseudo F statistic was suggested by Caliński and Harabasz (1974). See Milligan and Cooper (1985) and Cooper and Milligan (1988) regarding the use of the pseudo F statistic in estimating the number of clusters. See Example 31.2 in Chapter 31: The CLUSTER Procedure, for a comparison of pseudo F statistics.
-
Observed Overall R-Square, if you specify the SUMMARY option
-
Approximate Expected Overall R-Square, the approximate expected value of the overall R square under the uniform null hypothesis assuming that the variables are uncorrelated. The value is missing if the number of clusters is greater than one-fifth the number of observations.
-
Cubic Clustering Criterion, computed under the assumption that the variables are uncorrelated. The value is missing if the number of clusters is greater than one-fifth the number of observations.
If you are interested in the approximate expected R square or the cubic clustering criterion but your variables are correlated, you should cluster principal component scores from the PRINCOMP procedure. Both of these statistics are described by Sarle (1983). The performance of the cubic clustering criterion in estimating the number of clusters is examined by Milligan and Cooper (1985) and Cooper and Milligan (1988).
-
Distances Between Cluster Means, if you specify the DISTANCE option
Unless you specify the SHORT or SUMMARY option, PROC FASTCLUS displays the following:
-
Cluster Means for each variable
-
Cluster Standard Deviations for each variable
