The MCMC Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics
How PROC MCMC WorksBlocking of ParametersSampling MethodsTuning the Proposal DistributionDirect SamplingConjugate SamplingInitial Values of the Markov ChainsAssignments of ParametersStandard DistributionsUsage of Multivariate DistributionsSpecifying a New DistributionUsing Density Functions in the Programming StatementsTruncation and CensoringSome Useful SAS FunctionsMatrix Functions in PROC MCMCCreate Design MatrixModeling Joint LikelihoodRegenerating Diagnostics PlotsCaterpillar PlotAutocall Macros for PostprocessingGamma and Inverse-Gamma DistributionsPosterior Predictive DistributionHandling of Missing DataFunctions of Random-Effects ParametersFloating Point Errors and OverflowsHandling Error MessagesComputational ResourcesDisplayed OutputODS Table NamesODS Graphics -
Examples
 Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics
Simulating Samples From a Known DensityBox-Cox TransformationLogistic Regression Model with a Diffuse PriorLogistic Regression Model with Jeffreys’ PriorPoisson RegressionNonlinear Poisson Regression ModelsLogistic Regression Random-Effects ModelNonlinear Poisson Regression Multilevel Random-Effects ModelMultivariate Normal Random-Effects ModelMissing at Random AnalysisNonignorably Missing Data (MNAR) AnalysisChange Point ModelsExponential and Weibull Survival AnalysisTime Independent Cox ModelTime Dependent Cox ModelPiecewise Exponential Frailty ModelNormal Regression with Interval CensoringConstrained AnalysisImplement a New Sampling AlgorithmUsing a Transformation to Improve MixingGelman-Rubin Diagnostics - References
Blocking of Parameters
In a multivariate parameter model, if all k parameters are proposed with one joint distribution ![]() , acceptance or rejection would occur for all of them. This can be rather inefficient, especially when parameters have vastly
different scales. A way to avoid this difficulty is to allocate the k parameters into d blocks and update them separately. The PARMS statement puts model parameters in separate blocks, and each block of parameters is updated sequentially in the procedure.
, acceptance or rejection would occur for all of them. This can be rather inefficient, especially when parameters have vastly
different scales. A way to avoid this difficulty is to allocate the k parameters into d blocks and update them separately. The PARMS statement puts model parameters in separate blocks, and each block of parameters is updated sequentially in the procedure.
Suppose you want to sample from a multivariate distribution with probability density function ![]() where
where ![]() Now suppose that these k parameters are separated into d blocks—for example,
Now suppose that these k parameters are separated into d blocks—for example, ![]() where
where ![]() , where each
, where each ![]() contains a nonempty subset of the
contains a nonempty subset of the ![]() , and where each
, and where each ![]() is contained in one and only one
is contained in one and only one ![]() . In the MCMC context, the z’s are blocks of parameters. In the blocked algorithm, a proposal consists of several parts. Instead of proposing a simultaneous
move for all the
. In the MCMC context, the z’s are blocks of parameters. In the blocked algorithm, a proposal consists of several parts. Instead of proposing a simultaneous
move for all the ![]() ’s, a proposal is made for the
’s, a proposal is made for the ![]() ’s in
’s in ![]() only, then for the
only, then for the ![]() ’s in
’s in ![]() , and so on for d subproposals. Any accepted proposal can involve any number of the blocks moving. The parameters do not necessarily all move
at once as in the all-at-once Metropolis algorithm.
, and so on for d subproposals. Any accepted proposal can involve any number of the blocks moving. The parameters do not necessarily all move
at once as in the all-at-once Metropolis algorithm.
Formally, the blocked Metropolis algorithm is as follows. Let ![]() be the collection of
be the collection of ![]() that are in block
that are in block ![]() , and let
, and let ![]() be a symmetric multivariate distribution that is centered at the current values of
be a symmetric multivariate distribution that is centered at the current values of ![]() .
.
-
Let
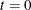 . Choose points for all
. Choose points for all 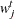 . A point can be an arbitrary point as long as
. A point can be an arbitrary point as long as 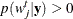 .
.
-
For
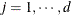 :
:
-
Generate a new sample,
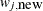 , using the proposal distribution
, using the proposal distribution 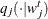 .
.
-
Calculate the following quantity:
![\[ r = \min \left\{ \frac{p(w_{j, \mbox{new}} | w_1^{t}, \cdots , w_{j-1}^{t}, w_{j+1}^{t-1}, \cdots , w_ d^{t}, {\mb {y}})}{p(w^{t}_{j}| w_1^{t}, \cdots , w_{j-1}^{t}, w_{j-1}^{t+1}, \cdots , w_ d^{t}, {\mb {y}})}, 1 \right\} . \]](images/statug_mcmc0191.png)
-
Sample u from the uniform distribution
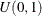 .
.
-
Set
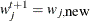 if
if 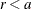 ;
; 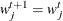 otherwise.
otherwise.
-
-
Set
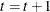 . If
. If 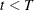 , the number of desired samples, go back to Step 2; otherwise, stop.
, the number of desired samples, go back to Step 2; otherwise, stop.
With PROC MCMC, you can sample all parameters simultaneously by putting them all in a single PARMS statement, you can sample
parameters individually by putting each parameter in its own PARMS statement, or you can sample certain subsets of parameters
together by grouping each subset in its own PARMS statements. For example, if the model you are interested in has five parameters,
alpha, beta, gamma, phi, sigma, the all-at-once strategy is as follows:
parms alpha beta gamma phi sigma;
The one-at-a-time strategy is as follows:
parms alpha; parms beta; parms gamma; parms phi; parms sigma;
A two-block strategy could be as follows:
parms alpha beta gamma; parms phi sigma;
The exceptions to the previously described blocking strategies are parameters that are sampled directly (either from their full conditional or marginal distributions) and parameters that are array-based (with multivariate prior distributions). In these cases, the parameters are taken out of an existing block and are updated individually. You can use the sampling options in the PARMS statement to override the default behavior.
One of the greatest challenges in MCMC sampling is achieving good mixing of the chains—the chains should quickly traverse the support of the stationary distribution. A number of factors determine the behavior of a Metropolis sampler; blocking is one of them, so you want to be extremely careful when you choose a good design. Generally speaking, forming blocks of parameters has its advantages, but it is not true that the larger the block the faster the convergence.
When simultaneously sampling a large number of parameters, the algorithm might find it difficult to achieve good mixing. As
the number of parameters gets large, it is much more likely to have (proposal) samples that fall well into the tails of the
target distribution, producing too small a test ratio. As a result, few proposed values are accepted and convergence is slow.
On the other hand, when the algorithm samples each parameter individually, the computational cost increases linearly. Each
block of Metropolis parameters requires one additional pass through the data set, so a five-block updating strategy could
take five times longer than a single-block updating strategy. In addition, there is a chance that the chain might mix far
too slowly because the conditional distributions (of ![]() given all other
given all other ![]() ’s) might be very “narrow,” as a result of posterior correlation among the parameters. When that happens, it takes a long time for the chain to fully
explore that dimension alone. There are no theoretical results that can help determine an optimal “blocking” for an arbitrary parametric model. A rule followed in practice is to form small groups of correlated parameters that belong
to the same context in the formulation of the model. The best mixing is usually obtained with a blocking strategy somewhere
between the all-at-once and one-at-a-time strategies.
’s) might be very “narrow,” as a result of posterior correlation among the parameters. When that happens, it takes a long time for the chain to fully
explore that dimension alone. There are no theoretical results that can help determine an optimal “blocking” for an arbitrary parametric model. A rule followed in practice is to form small groups of correlated parameters that belong
to the same context in the formulation of the model. The best mixing is usually obtained with a blocking strategy somewhere
between the all-at-once and one-at-a-time strategies.