The HPMIXED Procedure
Assumptions and Notation
The linear mixed models fit by the HPMIXED procedure can be represented as linear statistical models in the following form:
|
|
|
|
|
|
|
|
|
|
|
|
The symbols in these expressions denote the following:
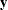
-
the
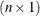 vector of responses
vector of responses
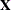
-
the
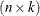 design matrix for the fixed effects
design matrix for the fixed effects
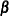
-
the
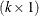 vector of fixed-effects parameters
vector of fixed-effects parameters
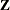
-
the
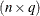 design matrix for the random effects
design matrix for the random effects
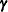
-
the
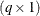 vector of random effects
vector of random effects

-
the
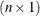 vector of unobservable residual errors
vector of unobservable residual errors
As is customary for statistical models in the linear mixed model family, the random effects are assumed normally distributed.
The same holds for the residual errors and these are furthermore distributed independently of the random effects. As a consequence,
these assumptions imply that the response vector ![]() has a multivariate normal distribution.
has a multivariate normal distribution.
Further assumptions, implicit in the preceding expression, are as follows:
-
The conditional mean of the data—given the random effects—is linear in the fixed effects and the random effects.
-
The marginal mean of the data is linear in the fixed-effects parameters.
