The VARIOGRAM Procedure
Example 98.2 An Anisotropic Case Study with Surface Trend in the Data
This example shows how to examine data for nonrandom surface trends and anisotropy. You use simulated data where the variable is atmospheric ozone (O
) concentrations measured in Dobson units (DU). The coordinates are offsets from a point in the southwest corner of the measurement area, with the east and north distances in units of kilometers (km). You work with the ozoneSet data set that contains 300 measurements in a square area of 100 km 
100 km.
The following statements read the data set:
title 'Semivariogram Analysis in Anisotropic Case With Trend Removal';
data ozoneSet;
input East North Ozone @@;
datalines;
34.9 68.2 286 39.2 12.5 270 44.4 37.7 275 90.5 27.0 282
91.1 40.8 285 98.6 61.6 294 61.8 26.7 281 64.0 11.5 274
22.4 26.5 274 89.3 18.3 279 32.3 28.3 274 31.1 53.1 279
43.0 17.5 272 79.3 42.3 283 99.9 57.9 291 1.8 24.1 273
81.7 73.5 294 22.9 32.0 273 64.9 67.5 292 76.5 56.3 285
78.7 11.7 276 61.8 99.3 307 49.1 86.6 299 40.0 35.8 273
69.3 3.8 278 23.4 9.3 270 66.3 94.3 304 71.3 6.5 275
9.7 54.4 280 85.2 81.7 300 30.3 60.9 284 94.6 94.3 309
10.6 10.3 271 73.0 43.0 280 4.9 50.7 280 19.0 79.4 289
2.4 73.1 287 77.7 25.2 278 8.4 27.1 276 93.5 19.7 279
0.2 34.5 275 50.4 91.3 302 55.7 26.2 279 50.3 2.3 274
16.3 84.4 293 19.0 6.9 272 57.1 92.3 303 61.0 0.4 275
10.7 18.7 271 15.2 43.5 277 67.0 87.4 301 79.0 54.0 285
36.0 53.3 279 58.3 52.1 282 56.6 79.7 294 40.4 32.4 275
48.9 64.1 286 54.0 54.9 281 27.5 48.5 279 36.4 30.3 275
10.5 31.0 273 87.0 39.4 283 47.9 37.5 274 64.7 63.4 288
0.5 90.8 294 22.8 22.4 275 31.1 78.8 291 93.6 49.8 290
2.5 39.3 273 83.6 25.6 282 49.8 24.1 278 73.1 91.8 305
30.5 90.6 297 26.0 61.2 284 58.4 66.2 289 30.5 4.3 273
38.3 85.6 298 89.2 96.6 309 53.4 6.3 275 27.3 12.8 271
43.4 56.5 281 99.5 86.9 305 85.8 22.8 281 83.0 10.9 278
24.8 16.7 271 51.1 18.8 275 59.0 54.3 283 35.5 91.4 298
18.1 56.0 279 78.0 36.4 277 56.8 6.9 275 21.1 44.5 277
73.9 75.9 296 54.2 0.1 274 33.2 75.1 290 38.2 3.3 274
15.2 14.7 272 15.9 84.2 292 60.2 95.2 304 9.8 27.2 276
91.2 56.4 289 94.7 86.9 303 56.7 49.6 281 24.2 9.5 270
43.0 17.0 272 85.9 10.7 278 53.9 41.1 276 30.4 63.4 286
62.8 86.3 299 76.8 24.6 279 31.6 94.0 300 26.9 73.8 287
18.9 68.4 284 99.4 37.2 285 79.1 3.3 277 34.9 74.7 289
6.4 33.8 277 48.4 82.2 294 86.0 58.0 289 92.0 60.4 293
50.2 91.6 300 12.2 38.3 275 72.7 48.9 283 82.7 34.1 279
77.0 51.0 286 86.6 15.8 278 42.0 42.7 277 99.3 8.2 278
17.4 70.6 286 11.2 92.4 295 60.2 28.8 280 92.0 73.3 297
25.3 30.6 273 36.6 8.9 274 34.2 4.4 273 26.6 54.7 278
1.7 27.4 278 49.6 1.1 275 62.8 89.3 301 28.0 49.3 279
51.2 75.1 293 59.3 93.5 304 83.6 90.5 304 79.4 87.0 302
78.0 28.3 281 16.8 19.1 272 9.1 81.2 292 23.7 55.8 277
75.5 21.3 279 64.4 43.3 279 38.9 98.9 303 22.5 87.9 293
96.7 37.9 285 92.3 93.9 308 16.9 25.4 273 15.2 61.5 283
73.8 94.0 306 57.4 97.2 305 73.2 4.9 276 39.2 82.3 294
95.7 99.4 315 66.0 98.4 306 95.3 26.9 283 45.4 75.3 291
64.8 15.4 276 69.8 55.4 284 36.3 74.9 290 9.9 22.2 276
65.8 13.9 276 13.0 82.0 293 95.6 77.2 301 32.5 55.6 279
45.8 35.5 275 62.2 6.6 274 25.2 51.2 279 92.4 8.1 277
40.5 35.3 273 9.9 3.9 271 43.5 44.0 278 68.6 61.3 287
64.2 77.5 296 57.6 81.6 294 69.5 64.7 291 64.3 95.1 304
2.8 62.4 283 33.2 83.3 294 10.7 71.0 285 24.3 88.2 294
94.5 32.2 283 21.0 67.6 286 20.1 71.6 286 85.2 71.3 296
94.8 30.7 283 53.4 92.0 301 81.0 50.0 287 54.6 29.9 277
71.1 90.1 303 15.2 2.9 271 83.6 17.8 278 76.0 21.8 279
55.6 37.4 275 86.7 83.7 303 43.6 83.6 295 44.2 31.7 274
90.0 83.3 300 6.2 0.5 270 42.2 87.7 298 31.7 4.3 273
91.4 41.2 285 78.0 50.6 286 27.1 56.1 278 72.6 63.9 291
29.3 49.9 281 49.0 36.9 275 13.9 53.5 280 93.1 83.2 300
73.0 61.6 289 63.1 27.5 280 38.3 72.5 287 72.7 34.2 277
6.9 32.3 274 17.1 58.6 280 19.6 94.6 297 2.7 36.5 276
34.5 5.5 275 98.6 95.9 313 9.1 71.1 285 88.6 55.8 287
26.8 78.5 289 64.8 66.6 292 59.7 25.7 280 47.3 70.2 288
6.1 94.4 296 50.5 82.7 296 9.1 41.6 276 86.0 71.0 296
75.2 69.8 293 73.3 84.8 300 42.5 15.9 274 56.1 76.1 292
87.9 41.2 285 65.1 9.8 274 79.0 41.2 282 44.6 65.1 287
54.7 68.3 289 57.0 26.8 279 8.7 12.3 270 33.7 61.9 286
25.0 55.8 278 69.3 94.9 306 49.2 64.6 287 78.2 93.7 307
47.9 26.6 277 96.9 51.4 292 39.6 73.4 287 37.9 66.1 285
94.5 71.4 296 51.6 18.3 276 37.6 73.2 287 68.5 10.7 274
46.7 9.6 273 87.4 38.9 282 45.6 43.9 277 70.7 76.9 296
82.8 53.6 287 82.5 55.4 286 37.8 5.1 275 89.8 96.1 309
63.9 4.9 276 2.0 11.7 270 31.3 59.2 282 93.9 65.3 296
47.9 93.0 301 29.9 36.0 274 14.6 28.3 274 17.5 70.1 286
2.6 68.5 282 23.1 12.0 268 36.8 20.4 273 80.9 9.0 276
39.2 0.0 274 26.2 44.3 276 81.9 12.9 277 3.2 21.4 272
76.9 76.7 297 88.6 7.7 277 9.7 8.4 273 26.7 91.5 296
73.8 6.1 276 33.7 39.3 276 64.0 58.4 286 5.7 91.2 295
85.8 93.8 307 85.8 39.1 281 93.9 63.4 295 53.1 46.3 278
51.9 42.9 277 16.8 75.7 288 29.2 66.9 285 37.4 72.5 287
;
The initial step is to explore the data set by inspecting the data spatial distribution. Run PROC VARIOGRAM, specifying the NOVARIOGRAM option in the COMPUTE statement as follows:
ods graphics on;
proc variogram data=ozoneSet; compute novariogram nhc=35; coord xc=East yc=North; var Ozone; run;
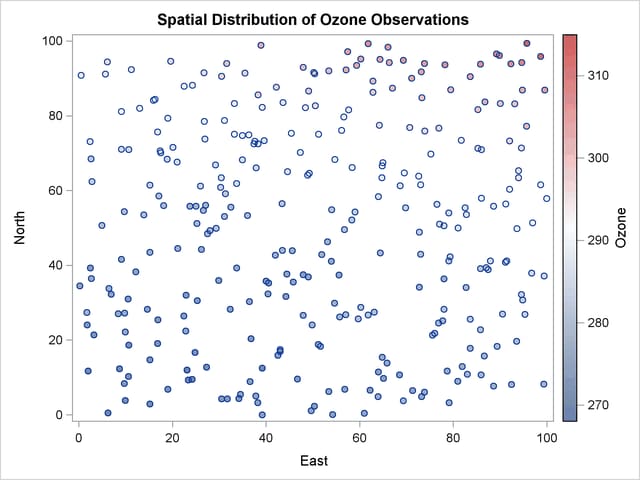
The result is a scatter plot of the observed data shown in Output 98.2.1. The scatter plot suggests an almost uniform spread of the measurements throughout the prediction area. No direct inference can be made about the existence of a surface trend in the data. However, the apparent stratification of ozone values in the northeast–southwest direction might indicate a nonrandom trend.
You need to define the size and count of the data classes by specifying suitable values for the LAGDISTANCE= and MAXLAGS= options, respectively. Compared to the smaller sample of thickness data used in Getting Started: VARIOGRAM Procedure, the larger size of the ozoneSet data results in more densely populated distance classes for the same value of the NHCLASSES= option. After you experiment with a variety of values for the NHCLASSES= option, you can adjust LAGDISTANCE= to have a relatively small number. Then you can account for a large value of MAXLAGS= so that you obtain many sample semivariogram points within your data correlation range. Specifying these values requires some exploration, for which you might need to return to this point from a later stage in your semivariogram analysis. For illustration purposes you now specify NHCLASSES=35.
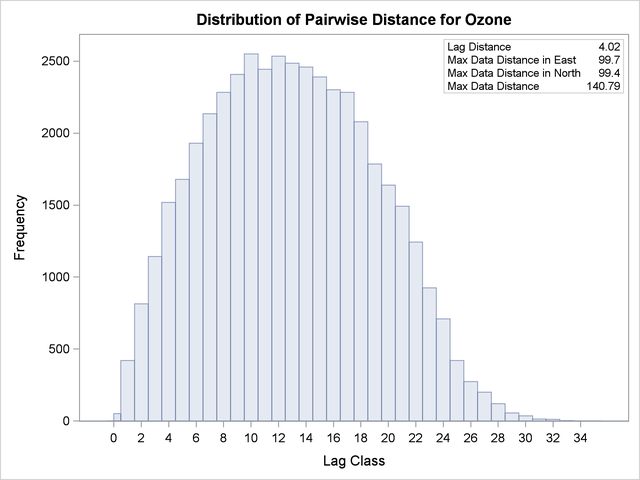
Your choice of NHCLASSES=35 yields the pairwise distance intervals table in Output 98.2.2 and the corresponding histogram in Output 98.2.3.
| Pairwise Distance Intervals | ||||
|---|---|---|---|---|
| Lag Class |
Bounds | Number of Pairs | Percentage of Pairs |
|
| 0 | 0.00 | 2.01 | 52 | 0.12% |
| 1 | 2.01 | 6.03 | 420 | 0.94% |
| 2 | 6.03 | 10.06 | 815 | 1.82% |
| 3 | 10.06 | 14.08 | 1143 | 2.55% |
| 4 | 14.08 | 18.10 | 1518 | 3.38% |
| 5 | 18.10 | 22.12 | 1680 | 3.75% |
| 6 | 22.12 | 26.15 | 1931 | 4.31% |
| 7 | 26.15 | 30.17 | 2135 | 4.76% |
| 8 | 30.17 | 34.19 | 2285 | 5.09% |
| 9 | 34.19 | 38.21 | 2408 | 5.37% |
| 10 | 38.21 | 42.24 | 2551 | 5.69% |
| 11 | 42.24 | 46.26 | 2444 | 5.45% |
| 12 | 46.26 | 50.28 | 2535 | 5.65% |
| 13 | 50.28 | 54.30 | 2487 | 5.55% |
| 14 | 54.30 | 58.33 | 2460 | 5.48% |
| 15 | 58.33 | 62.35 | 2391 | 5.33% |
| 16 | 62.35 | 66.37 | 2302 | 5.13% |
| 17 | 66.37 | 70.39 | 2285 | 5.09% |
| 18 | 70.39 | 74.41 | 2079 | 4.64% |
| 19 | 74.41 | 78.44 | 1786 | 3.98% |
| 20 | 78.44 | 82.46 | 1640 | 3.66% |
| 21 | 82.46 | 86.48 | 1493 | 3.33% |
| 22 | 86.48 | 90.50 | 1243 | 2.77% |
| 23 | 90.50 | 94.53 | 925 | 2.06% |
| 24 | 94.53 | 98.55 | 710 | 1.58% |
| 25 | 98.55 | 102.57 | 421 | 0.94% |
| 26 | 102.57 | 106.59 | 274 | 0.61% |
| 27 | 106.59 | 110.62 | 200 | 0.45% |
| 28 | 110.62 | 114.64 | 120 | 0.27% |
| 29 | 114.64 | 118.66 | 55 | 0.12% |
| 30 | 118.66 | 122.68 | 35 | 0.08% |
| 31 | 122.68 | 126.71 | 14 | 0.03% |
| 32 | 126.71 | 130.73 | 11 | 0.02% |
| 33 | 130.73 | 134.75 | 2 | 0.00% |
| 34 | 134.75 | 138.77 | 0 | 0.00% |
| 35 | 138.77 | 142.80 | 0 | 0.00% |
Notice the overall high pair count in the majority of classes in Output 98.2.2. You can see that even for higher values of NHCLASSES= the classes are still sufficiently populated for your semivariogram analysis according to the rule of thumb stated in the section Choosing the Size of Classes. Based on the displayed information in Output 98.2.3, you specify LAGDISTANCE=4 km. You can further experiment with smaller lag sizes to obtain more points in your sample semivariogram.
You can focus on the MAXLAGS= specification at a later point. The important step now is to investigate the presence of trends in the measurement. The following section makes a suggestion about how to remove surface trends from your data and then continues the semivariogram analysis with the detrended data.
