The VARIOGRAM Procedure
Autocorrelation Statistics Types
One measure of spatial autocorrelation provided by PROC VARIOGRAM is Moran’s  statistic, which was introduced by Moran (1950) and is defined as
statistic, which was introduced by Moran (1950) and is defined as
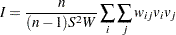 |
where 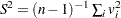 , and
, and 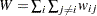 .
.
Another measure of spatial autocorrelation in PROC VARIOGRAM is Geary’s  statistic (Geary; 1954), defined as
statistic (Geary; 1954), defined as
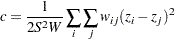 |
These expressions indicate that Moran’s  coefficient makes use of the centered variable, whereas the Geary’s
coefficient makes use of the centered variable, whereas the Geary’s  expression uses the noncentered values in the summation.
expression uses the noncentered values in the summation.
Inference on these two statistic types comes from approximate tests based on the asymptotic distribution of  and
and  , which both tend to a normal distribution as
, which both tend to a normal distribution as  increases. To this end, PROC VARIOGRAM calculates the means and variances of
increases. To this end, PROC VARIOGRAM calculates the means and variances of  and
and  . The outcome depends on the assumption made regarding the distribution
. The outcome depends on the assumption made regarding the distribution 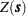 . In particular, you can choose to investigate any of the statistics under the normality (also known as Gaussianity) or the randomization assumption. Cliff and Ord (1981) provided the equations for the means and variances of the
. In particular, you can choose to investigate any of the statistics under the normality (also known as Gaussianity) or the randomization assumption. Cliff and Ord (1981) provided the equations for the means and variances of the  and
and  distributions, as described in the following.
distributions, as described in the following.
The normality assumption asserts that the random field 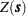 follows a normal distribution of constant mean (
follows a normal distribution of constant mean (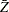 ) and variance, from which the
) and variance, from which the  values are drawn. In this case, the
values are drawn. In this case, the  statistics yield
statistics yield
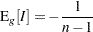 |
and
 |
where 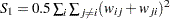 and
and 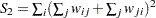 . The corresponding moments for the
. The corresponding moments for the  statistics are
statistics are
 |
and
 |
According to the randomization assumption, the  and
and  observations are considered in relation to all the different values that
observations are considered in relation to all the different values that  and
and  could take, respectively, if the
could take, respectively, if the 
 values were repeatedly randomly permuted around the domain
values were repeatedly randomly permuted around the domain 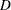 . The moments for the
. The moments for the  statistics are now
statistics are now
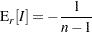 |
and
 |
where 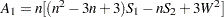 ,
, 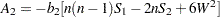 . The factor
. The factor 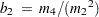 is the coefficient of kurtosis that uses the sample moments
is the coefficient of kurtosis that uses the sample moments 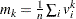 for
for 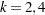 . Finally, the
. Finally, the  statistics under the randomization assumption are given by
statistics under the randomization assumption are given by
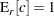 |
and
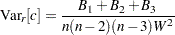 |
with 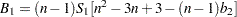 ,
, 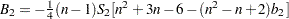 , and
, and 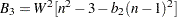 .
.
If you specify LAGDISTANCE= to be larger than the maximum data distance in your domain, the binary weighting scheme used by the VARIOGRAM procedure leads to all weights 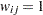 ,
,  . In this extreme case the preceding definitions can show that the variances of the
. In this extreme case the preceding definitions can show that the variances of the  and
and  statistics become zero under either the normality or the randomization assumption.
statistics become zero under either the normality or the randomization assumption.
A similar effect might occur when you have collocated observations (see the section Pair Formation). The Moran’s  and Geary’s
and Geary’s  statistics allow for the inclusion of such pairs in the computations. Hence, contrary to the semivariance analysis, PROC VARIOGRAM does not exclude pairs of collocated data from the autocorrelation statistics.
statistics allow for the inclusion of such pairs in the computations. Hence, contrary to the semivariance analysis, PROC VARIOGRAM does not exclude pairs of collocated data from the autocorrelation statistics.
