The SEQTEST Procedure
- Overview
- Getting Started
-
Syntax
-
Details
Input Data Sets Boundary Variables Information Level Adjustments at Future Stages Boundary Adjustments for Information Levels Boundary Adjustments for Minimum Error Spending Boundary Adjustments for Overlapping Lower and Upper beta Boundaries Stochastic Curtailment Repeated Confidence Intervals Analysis after a Sequential Test Available Sample Space Orderings in a Sequential Test Applicable Tests and Sample Size Computation Table Output ODS Table Names Graphics Output ODS Graphics Acknowledgments
-
Examples
Testing the Difference between Two Proportions Testing an Effect in a Regression Model Testing an Effect with Early Stopping to Accept H0 Testing a Binomial Proportion Comparing Two Proportions with a Log Odds Ratio Test Comparing Two Survival Distributions with a Log-Rank Test Testing an Effect in a Proportional Hazards Regression Model Testing an Effect in a Logistic Regression Model
- References
| Boundary Adjustments for Information Levels |
In a group sequential clinical trial, if the information level for the observed test statistic does not match the corresponding information level in the BOUNDARY= data set, the INFOADJ=PROP option (which is the default) can be used to modify information levels at future stages to accommodate this observed information level. With the adjusted information levels, the ERRSPENDADJ= option provides various methods to compute error spending values at the current and future interim stages. These error spending values are then used to derive boundary values in the SEQTEST procedure. See the section "Error Spending Methods" in the chapter "The SEQDESIGN Procedure" for a detailed description of how to use these error spending values to derive boundary values.
The ERRSPENDADJ=NONE option keeps the error spending the same at each stage. The ERRSPENDADJ=ERRLINE option uses a linear interpolation on the cumulative error spending in the design stored in the BOUNDARY= data set to derive the error spending for each unmatched information level (Kittelson and Emerson 1999, p. 882). That is, the cumulative error spending for an information level 
is computed as
 |
where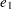 
, 
, ..., 
are the cumulative errors at the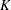 
stages of the design that is stored in the BOUNDARY= data set.
The ERRSPENDADJ=ERRFUNCPOC option uses Pocock-type cumulative error spending function (Lan and DeMets 1983):
 |
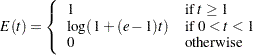With an error level of 
or 
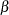, the cumulative error spending for an information level is 
or 
.
The ERRSPENDADJ=ERRFUNCOBF option uses O’Brien-Fleming-type cumulative error spending function (Lan and DeMets 1983):
 |
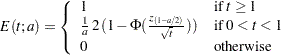where 
is either for the spending function or 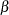for the 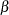spending function, and 
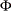is the cumulative distribution function of the standardized 
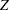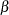statistic. That is, with an error level of or , the cumulative error spending for an information level is 
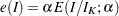or 
.
The ERRSPENDADJ=ERRFUNCGAMMA option uses gamma cumulative error spending function (Hwang, Shih, and DeCani 1990):
 |
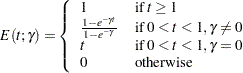where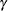 
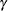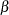is the parameter specified in the GAMMA= option. That is, with an error level of or , the cumulative error spending for an information level is 
or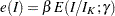 
.
The ERRSPENDADJ=ERRFUNCPOW option uses power cumulative error spending function (Jennison and Turnbull 2000, p. 148):
 |
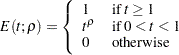where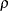 
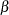is the power parameter specified in the RHO= suboption. With an error level of or , the cumulative error spending for an information level is 
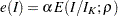or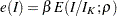 
.
If the BOUNDARYKEY=BOTH option is specified, the maximum information required for the trial might not be the same as the maximum information level stored in the BOUNDARY= data set. In this case, the information levels at future stages are adjusted proportionally, and the same error spending values that were computed based on the maximum information level stored in the BOUNDARY= data set are used to derive boundary values for the trial.
If an error spending function is used to create boundaries for the design in the SEQDESIGN procedure, then in order to better maintain the design features throughout the group sequential trial, the same error spending function to create boundaries for the design in the SEQDESIGN procedure should be used to modify boundaries in the SEQTEST procedure at each subsequent stage.