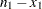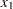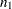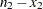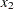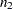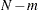The POWER Procedure
- Overview
-
Getting Started
-
Syntax
PROC POWER Statement LOGISTIC Statement MULTREG Statement ONECORR Statement ONESAMPLEFREQ Statement ONESAMPLEMEANS Statement ONEWAYANOVA Statement PAIREDFREQ Statement PAIREDMEANS Statement PLOT Statement TWOSAMPLEFREQ Statement TWOSAMPLEMEANS Statement TWOSAMPLESURVIVAL Statement TWOSAMPLEWILCOXON Statement
-
Details
Overview of Power Concepts Summary of Analyses Specifying Value Lists in Analysis Statements Sample Size Adjustment Options Error and Information Output Displayed Output ODS Table Names Computational Resources Computational Methods and Formulas ODS Graphics ODS Styles Suitable for Use with PROC POWER
-
Examples
One-Way ANOVA The Sawtooth Power Function in Proportion Analyses Simple AB/BA Crossover Designs Noninferiority Test with Lognormal Data Multiple Regression and Correlation Comparing Two Survival Curves Confidence Interval Precision Customizing Plots Binary Logistic Regression with Independent Predictors Wilcoxon-Mann-Whitney Test
- References
Analyses in the TWOSAMPLEFREQ Statement
Overview of th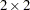e 
Table
Notation:
Outcome |
||||
Failure |
Success |
|||
Group |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
||
 |
 |
|||
 |
 |
|||
 |
 |
|||
 |
 |
|||
 |
 |
|||
 |
 |
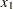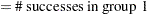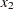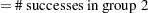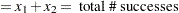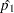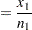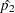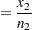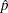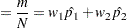The hypotheses are
 |
 |
|||
 |
 |
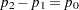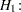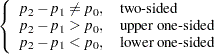where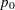 
is constrained to be 
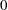for all but the unconditional Pearson chi-square test.
Internal calculations are performed in terms of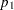 
, 
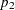, and 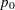. An input set consisting of 
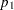, , and 
is transformed as follows:
 |
 |
|||
 |
 |
|||
 |
 |
|||
 |
 |
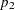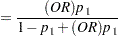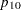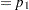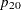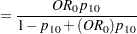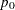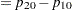An input set consisting of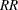 
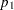, , and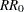 
is transformed as follows:
|
 |
|||
|
|
|||
|
 |
|||
|
|
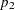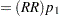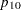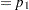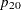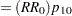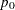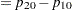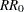Note that the transformation of either or to 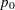is not unique. The chosen parameterization fixes the null value 
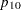at the input value of .
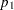Pearson Chi-Square Test for Two Proportions (TEST=PCHI)
The usual Pearson chi-square test is unconditional. The test statistic
 |
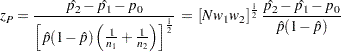is assumed to have a null distribution of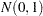 
.
Sample size for the one-sided cases is given by equation (4) in Fleiss, Tytun, and Ury (1980). One-sided power is computed as suggested by Diegert and Diegert (1981) by inverting the sample size formula. Power for the two-sided case is computed by adding the lower-sided and upper-sided powers each with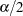 
, and sample size for the two-sided case is obtained by numerically inverting the power formula. A custom null value 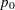for the proportion difference 
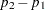is also supported.
 |
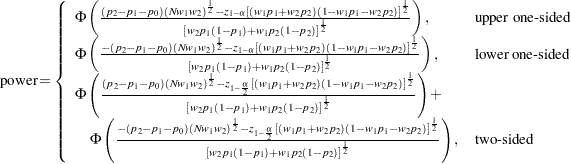For the one-sided cases, a closed-form inversion of the power equation yield an approximate total sample size
 |
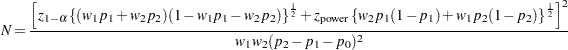For the two-sided case, the solution for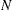 
is obtained by numerically inverting the power equation.
Likelihood Ratio Chi-Square Test for Two Proportions (TEST=LRCHI)
The usual likelihood ratio chi-square test is unconditional. The test statistic
 |
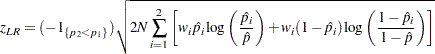is assumed to have a null distribution of 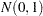and an alternative distribution of 
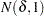, where
 |
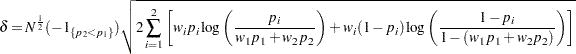The approximate power is
 |
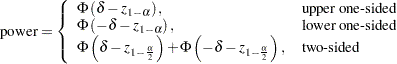For the one-sided cases, a closed-form inversion of the power equation yield an approximate total sample size
 |
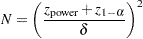For the two-sided case, the solution for 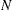is obtained by numerically inverting the power equation.
Fisher’s Exact Conditional Test for Two Proportions (Test=FISHER)
Fisher’s exact test is conditional on the observed total number of successes 
. Power and sample size computations are based on a test with similar power properties, the continuity-adjusted arcsine test. The test statistic
 |
 |
|||
 |
 |
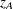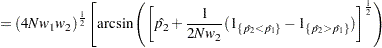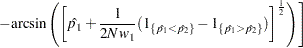is assumed to have a null distribution of 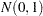and an alternative distribution of 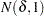, where
 |
 |
|||
|
 |
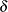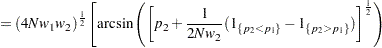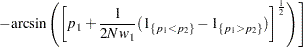The approximate power for the one-sided balanced case is given by Walters (1979) and is easily extended to the unbalanced and two-sided cases:
|
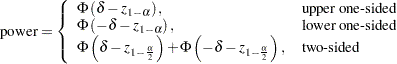