The POWER Procedure

Fisher’s z Test for Pearson Correlation (TEST=PEARSON DIST=FISHERZ)

Fisher’s transformation (Fisher 1921) of the sample correlation is defined as

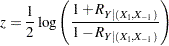Fisher’s test assumes the approximate normal distribution 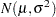for , where

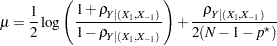and

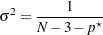where 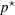is the number of variables partialed out (Anderson 1984, pp. 132–133) and 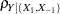is the partial correlation between and 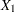adjusting for the set of zero or more variables .

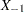The test statistic

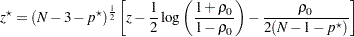is assumed to have a normal distribution 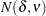, where 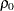is the null partial correlation 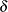and and are derived from Section 16.33 of Stuart and Ord (1994):

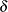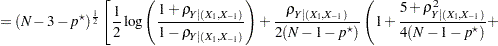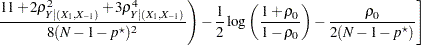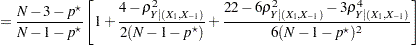The approximate power is computed as

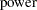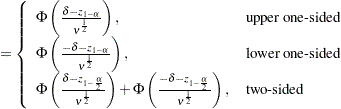Because the test is biased, the achieved significance level might differ from the nominal significance level. The actual alpha is computed in the same way as the power except with the correlation 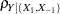replaced by the null correlation .

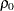t Test for Pearson Correlation (TEST=PEARSON DIST=T)

The two-sided case is identical to multiple regression with an intercept and 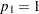, which is discussed in the section Analyses in the MULTREG Statement.

Let 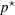denote the number of variables partialed out. For the one-sided cases, the test statistic is

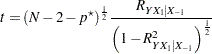which is assumed to have a null distribution of .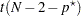

If the and variables are assumed to have a joint multivariate normal distribution, then the exact power is given by the following formula:

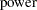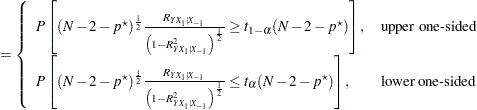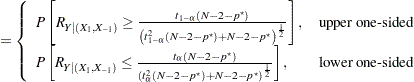The distribution of (given the underlying true correlation 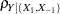) is given in Chapter 32 of Johnson, Kotz, and Balakrishnan (1995).

If the variables are assumed to have fixed values, then the exact power is given by the noncentral distribution 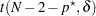, where the noncentrality is

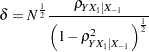The power is
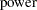
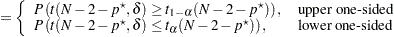