The ORTHOREG Procedure
Example 65.2 Wampler Data
This example applies the ORTHOREG procedure to a collection of data sets noted for being ill-conditioned. The OUTEST= data set is used to collect the results for comparison with values certified to be correct by the National Institute of Standards and Technology (1998).
Note: The results from this example vary from machine to machine, depending on floating-point configuration.
The data are from Wampler (1970). The independent variates for all five data sets are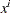 
, 
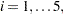for 
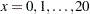. Two of the five dependent variables are exact linear functions of the independent terms:
 |
 |
 |
|||
 |
|
 |
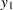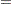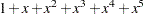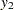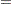The other three dependent variables have the same mean value as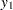 
, but with nonzero errors:
 |
|
 |
|||
 |
|
 |
|||
 |
|
 |
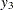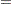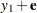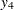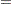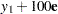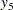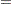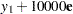where 
is a vector of values with standard deviation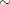 
2044, chosen to be orthogonal to the mean model for .
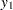The following statements create a SAS data set Wampler that contains the Wampler data, run a SAS macro program that uses PROC ORTHOREG to fit a fifth-order polynomial in 
to each of the Wampler dependent variables, and collect the results in a data set named ParmEst:
data Wampler;
do x=0 to 20;
input e @@;
y1 = 1 + x + x**2 + x**3
+ x**4 + x**5;
y2 = 1 + .1 *x + .01 *x**2 + .001*x**3
+ .0001*x**4 + .00001*x**5;
y3 = y1 + e;
y4 = y1 + 100*e;
y5 = y1 + 10000*e;
output;
end;
datalines;
759 -2048 2048 -2048 2523 -2048 2048 -2048 1838 -2048 2048
-2048 1838 -2048 2048 -2048 2523 -2048 2048 -2048 759
;
%macro WTest;
data ParmEst; if (0); run;
%do i = 1 %to 5;
proc orthoreg data=Wampler outest=ParmEst&i noprint;
model y&i = x x*x x*x*x x*x*x*x x*x*x*x*x;
data ParmEst&i; set ParmEst&i; Dep = "y&i";
data ParmEst; set ParmEst ParmEst&i;
label Col1='x' Col2='x**2' Col3='x**3'
Col4='x**4' Col5='x**5';
run;
%end;
%mend;
%WTest;
Instead of displaying the raw values of the RMSE and parameter estimates, use an additional DATA step as follows to compute the deviations from the values certified to be correct by the National Institute of Standards and Technology (1998):
data ParmEst; set ParmEst;
if (Dep = 'y1') then
_RMSE_ = _RMSE_ - 0.00000000000000;
else if (Dep = 'y2') then
_RMSE_ = _RMSE_ - 0.00000000000000;
else if (Dep = 'y3') then
_RMSE_ = _RMSE_ - 2360.14502379268;
else if (Dep = 'y4') then
_RMSE_ = _RMSE_ - 236014.502379268;
else if (Dep = 'y5') then
_RMSE_ = _RMSE_ - 23601450.2379268;
if (Dep ^= 'y2') then do;
Intercept = Intercept - 1.00000000000000;
Col1 = Col1 - 1.00000000000000;
Col2 = Col2 - 1.00000000000000;
Col3 = Col3 - 1.00000000000000;
Col4 = Col4 - 1.00000000000000;
Col5 = Col5 - 1.00000000000000;
end;
else do;
Intercept = Intercept - 1.00000000000000;
Col1 = Col1 - 0.100000000000000;
Col2 = Col2 - 0.100000000000000e-1;
Col3 = Col3 - 0.100000000000000e-2;
Col4 = Col4 - 0.100000000000000e-3;
Col5 = Col5 - 0.100000000000000e-4;
end;
run;
proc print data=ParmEst label noobs; title 'Wampler data: Deviations from Certified Values'; format _RMSE_ Intercept Col1-Col5 e9.; var Dep _RMSE_ Intercept Col1-Col5; run;
The results, shown in Output 65.2.1, indicate that the values computed by PROC ORTHOREG are quite close to the NIST-certified values.
| Wampler data: Deviations from Certified Values |
| Dep | _RMSE_ | Intercept | x | x**2 | x**3 | x**4 | x**5 |
|---|---|---|---|---|---|---|---|
| y1 | 0.00E+00 | 5.46E-12 | -9.82E-11 | 1.55E-11 | -5.68E-13 | 3.55E-14 | -6.66E-16 |
| y2 | 0.00E+00 | 8.88E-16 | -3.19E-15 | 1.24E-15 | -1.88E-16 | 1.20E-17 | -2.57E-19 |
| y3 | -2.09E-11 | -7.73E-11 | 1.46E-11 | -2.09E-11 | 2.50E-12 | -1.28E-13 | 2.66E-15 |
| y4 | -4.07E-10 | -5.38E-10 | 8.99E-10 | -3.29E-10 | 4.23E-11 | -2.27E-12 | 4.35E-14 |
| y5 | -3.35E-08 | -4.10E-08 | 8.07E-08 | -2.77E-08 | 3.54E-09 | -1.90E-10 | 3.64E-12 |