PROC ORTHOREG: Precise Analysis of Variance :: SAS/STAT(R) 9.3 User's Guide

Example 65.1 Precise Analysis of Variance

The data for the following example are from Powell, Murphy, and Gramlich (1982). In order to calibrate an instrument for measuring atomic weight, 24 replicate measurements of the atomic weight of silver (chemical symbol Ag) are made with the new instrument and with a reference instrument.

Note: The results from this example vary from machine to machine, depending on floating-point configuration.

The following statements read the measurements for the two instruments into the SAS data set AgWeight:

title 'Atomic Weight of Silver by Two Different Instruments';
data AgWeight;
   input Instrument AgWeight @@;
   datalines;
1 107.8681568   1 107.8681465   1 107.8681572   1 107.8681785
1 107.8681446   1 107.8681903   1 107.8681526   1 107.8681494
1 107.8681616   1 107.8681587   1 107.8681519   1 107.8681486
1 107.8681419   1 107.8681569   1 107.8681508   1 107.8681672
1 107.8681385   1 107.8681518   1 107.8681662   1 107.8681424
1 107.8681360   1 107.8681333   1 107.8681610   1 107.8681477
2 107.8681079   2 107.8681344   2 107.8681513   2 107.8681197
2 107.8681604   2 107.8681385   2 107.8681642   2 107.8681365
2 107.8681151   2 107.8681082   2 107.8681517   2 107.8681448
2 107.8681198   2 107.8681482   2 107.8681334   2 107.8681609
2 107.8681101   2 107.8681512   2 107.8681469   2 107.8681360
2 107.8681254   2 107.8681261   2 107.8681450   2 107.8681368
;

Notice that the variation in the atomic weight measurements is several orders of magnitude less than their mean. This is a situation that can be difficult for standard, regression-based analysis-of-variance procedures to handle correctly.

The following statements invoke the ORTHOREG procedure to perform a simple one-way analysis of variance, testing for differences between the two instruments:

proc orthoreg data=AgWeight;
   class Instrument;
   model AgWeight = Instrument;
run;

Output 65.1.1 shows the resulting analysis.

Output 65.1.1 PROC ORTHOREG Results for Atomic Weight Example

Atomic Weight of Silver by Two Different Instruments

The ORTHOREG Procedure

Class Level Information
Factor	Levels	Values
Instrument	2	1	2

Atomic Weight of Silver by Two Different Instruments

The ORTHOREG Procedure

Dependent Variable: AgWeight

Source	DF	Sum of Squares	Mean Square	F Value	Pr > F
Model	1	3.6383419E-9	3.6383419E-9	15.95	0.0002
Error	46	1.0495173E-8	2.281559E-10
Corrected Total	47	1.4133515E-8

Root MSE	0.0000151048
R-Square	0.2574265445

Parameter	DF	Parameter Estimate	Standard Error	t Value	Pr > \|t\|
Intercept	1	107.868136354166	3.0832608E-6	3.499E7	<.0001
(Instrument='1')	1	0.00001741249999	4.3603893E-6	3.99	0.0002
(Instrument='2')	0	0	.	.	.

The mean difference between instruments is about $\text{[math]}$ (the value of the (Instrument=’1’) parameter in the parameter estimates table), whereas the level of background variation in the measurements is about 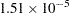$\text{[math]}$ (the value of the root mean square error). At this level of error, the difference is significant, with a $\text{[math]}$ -value of 0.0002.

The National Institute of Standards and Technology (1998) has provided certified ANOVA values for this data set. The following statements use ODS to examine the ANOVA values produced by both the ORTHOREG and GLM procedures more precisely for comparison with the NIST-certified values:

ods listing close;
ods output ANOVA         = OrthoregANOVA
           FitStatistics = OrthoregFitStat;

proc orthoreg data=AgWeight;
   class Instrument;
   model AgWeight = Instrument;
run;

ods output OverallANOVA  = GLMANOVA
           FitStatistics = GLMFitStat;
proc glm data=AgWeight;
   class Instrument;
   model AgWeight = Instrument;
run;
ods listing;

data _null_; set OrthoregANOVA  (in=inANOVA)
                 OrthoregFitStat(in=inFitStat);
   if (inANOVA) then do;
      if (Source = 'Model') then put "Model SS: " ss e20.;
      if (Source = 'Error') then put "Error SS: " ss e20.;
   end;
   if (inFitStat) then do;
      if (Statistic = 'Root MSE') then
                            put "Root MSE: " nValue1 e20.;
      if (Statistic = 'R-Square') then
                         put "R-Square: " nValue1 best20.;
   end;
data _null_; set GLMANOVA  (in=inANOVA)
                 GLMFitStat(in=inFitStat);
   if (inANOVA) then do;
      if (Source = 'Model') then put "Model SS: " ss e20.;
      if (Source = 'Error') then put "Error SS: " ss e20.;
   end;
   if (inFitStat) then      put "Root MSE: " RootMSE e20.;
   if (inFitStat) then   put "R-Square: " RSquare best20.;
run;

In SAS/STAT software prior to SAS 8, PROC GLM gave much less accurate results than PROC ORTHOREG. Table 65.8 and Table 65.9 compare the ANOVA values certified by NIST with those produced by the two procedures.

Table 65.8 Accuracy Comparison for Sums of Squares
Values	Model SS	Error SS
NIST-certified	3.6383418750000E $\text{[math]}$ 09	1.0495172916667E $\text{[math]}$ 08
ORTHOREG	3.6383418747907E $\text{[math]}$ 09	1.0495172916797E $\text{[math]}$ 08
GLM, since SAS 8	3.6383418747907E $\text{[math]}$ 09	1.0495172916797E $\text{[math]}$ 08
GLM, before SAS 8	0	1.0331496763990E $\text{[math]}$ 08

Table 65.9 Accuracy Comparison for Fit Statistics
Values	Root MSE	R Square
NIST-certified	1.5104831444641E $\text{[math]}$ 05	0.25742654453832
ORTHOREG	1.5104831444735E $\text{[math]}$ 05	0.25742654452494
GLM, since SAS 8	1.5104831444735E $\text{[math]}$ 05	0.25742654452494
GLM, before SAS 8	1.4986585859992E $\text{[math]}$ 05	0

Although the PROC ORTHOREG values and the PROC GLM values for the current version are quite close to the certified ones, the PROC GLM values for releases prior to SAS 8 are not. In fact, since the model sum of squares is so small, in prior releases the GLM procedure set it (and consequently R square) to zero.