PROC NESTED: Displayed Output :: SAS/STAT(R) 9.3 User's Guide

Displayed Output

PROC NESTED displays the following items for each dependent variable:

Coefficients of Expected Mean Squares, which are the coefficients of the 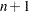$\text{[math]}$ variance components making up the expected mean square. Denoting the element in the 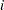$\text{[math]}$ th row and 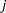$\text{[math]}$ th column of this matrix by 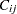$\text{[math]}$ , the expected value of the mean square due to the 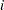$\text{[math]}$ th classification factor is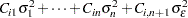

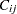$\text{[math]}$

$\text{[math]}$ is always zero for 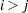$\text{[math]}$ , and if the design is balanced, 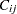$\text{[math]}$ is equal to the common size of all classification groups of the 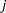$\text{[math]}$ th factor for 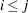$\text{[math]}$ . Finally, the mean square for error is always an unbiased estimate of 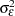$\text{[math]}$ . In other words, $\text{[math]}$ .

For every dependent variable, PROC NESTED displays an analysis of variance table. Each table contains the following:

each Variance Source in the model (the different components of variance) and the total variance
degrees of freedom (DF) for the corresponding sum of squares
Sum of Squares for each classification factor. The sum of squares for a given classification factor is the sum of squares in the dependent variable within the factors that precede it in the model, corrected for the factors that follow it. (See the section Computational Method.)
$\text{[math]}$ Value for a factor, which is the ratio of its mean square to the appropriate error mean square. The next column, labeled PR > F, gives the significance levels that result from testing the hypothesis that each variance component equals zero.
the appropriate Error Term for an $\text{[math]}$ test, which is the mean square due to the next classification factor in the nesting order. (See the section Error Terms in F Tests.)
Mean Square due to a factor, which is the corresponding sum of squares divided by the degrees of freedom
estimates of the Variance Components. These are computed by equating the mean squares to their expected values and solving for the variance terms. (See the section Computational Method.)
Percent of Total, the proportion of variance due to each source. For the 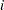$\text{[math]}$ th factor, the value is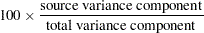

$\text{[math]}$
Mean, the overall average of the dependent variable. This gives an unbiased estimate of the mean of the population. Its variance is estimated by a certain linear combination of the estimated variance components, which is identical to the mean square due to the first factor in the model divided by the total number of observations when the design is balanced.

If there is more than one dependent variable, then the NESTED procedure displays an "analysis of covariation" table for each pair of dependent variables (unless the AOV option is specified in the PROC NESTED statement). See the section Analysis of Covariation for details. For each source of variation, this table includes the following:

Degrees of Freedom
Sum of Products
Mean Products
Covariance Component, the estimate of the covariance component

Items in the analysis of covariation table are computed analogously to their counterparts in the analysis of variance table. The analysis of covariation table also includes the following:

Variance Component Correlation for a given factor. This is an estimate of the correlation between corresponding effects due to this factor. This correlation is the ratio of the covariance component for this factor to the square root of the product of the variance components for the factor for the two different dependent variables. (See the section Analysis of Covariation.)
Mean Square Correlation for a given classification factor. This is the ratio of the Mean Products for this factor to the square root of the product of the Mean Squares for the factor for the two different dependent variables.

The NESTED Procedure