The MIANALYZE Procedure
- Overview
- Getting Started
-
Syntax

-
Details

-
Examples
 Reading Means and Standard Errors from Variables in a DATA= Data Set Reading Means and Covariance Matrices from a DATA= COV Data Set Reading Regression Results from a DATA= EST Data Set Reading Mixed Model Results from PARMS= and COVB= Data Sets Reading Generalized Linear Model Results Reading GLM Results from PARMS= and XPXI= Data Sets Reading Logistic Model Results from PARMS= and COVB= Data Sets Reading Mixed Model Results with Classification Variables Using a TEST statement Combining Correlation Coefficients
Reading Means and Standard Errors from Variables in a DATA= Data Set Reading Means and Covariance Matrices from a DATA= COV Data Set Reading Regression Results from a DATA= EST Data Set Reading Mixed Model Results from PARMS= and COVB= Data Sets Reading Generalized Linear Model Results Reading GLM Results from PARMS= and XPXI= Data Sets Reading Logistic Model Results from PARMS= and COVB= Data Sets Reading Mixed Model Results with Classification Variables Using a TEST statement Combining Correlation Coefficients - References
Example 57.2 Reading Means and Covariance Matrices from a DATA= COV Data Set
This example creates a COV-type data set that contains sample means and covariance matrices computed from imputed data sets. These estimates are then combined to generate valid statistical inferences about the population means.
The following statements use the CORR procedure to generate sample means and a covariance matrix for the variables in each imputed data set:
proc corr data=outmi cov nocorr noprint out=outcov(type=cov); var Oxygen RunTime RunPulse; by _Imputation_; run;
The following statements display (in Output 57.2.1) output sample means and covariance matrices from PROC CORR for the first two imputed data sets:
proc print data=outcov(obs=12);
title 'CORR Means and Covariance Matrices'
' (First Two Imputations)';
run;
| CORR Means and Covariance Matrices (First Two Imputations) |
| Obs | _Imputation_ | _TYPE_ | _NAME_ | Oxygen | RunTime | RunPulse |
|---|---|---|---|---|---|---|
| 1 | 1 | COV | Oxygen | 28.5603 | -7.2652 | -11.812 |
| 2 | 1 | COV | RunTime | -7.2652 | 2.5214 | 2.536 |
| 3 | 1 | COV | RunPulse | -11.8121 | 2.5357 | 79.271 |
| 4 | 1 | MEAN | 47.0120 | 10.4441 | 171.216 | |
| 5 | 1 | STD | 5.3442 | 1.5879 | 8.903 | |
| 6 | 1 | N | 31.0000 | 31.0000 | 31.000 | |
| 7 | 2 | COV | Oxygen | 27.1240 | -6.6761 | -10.217 |
| 8 | 2 | COV | RunTime | -6.6761 | 2.2035 | 2.611 |
| 9 | 2 | COV | RunPulse | -10.2170 | 2.6114 | 95.631 |
| 10 | 2 | MEAN | 47.2407 | 10.5040 | 171.244 | |
| 11 | 2 | STD | 5.2081 | 1.4844 | 9.779 | |
| 12 | 2 | N | 31.0000 | 31.0000 | 31.000 |
Note that the covariance matrices in the data set outcov are estimated covariance matrices of variables, 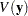 . The estimated covariance matrix of the sample means is
. The estimated covariance matrix of the sample means is 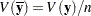 , where
, where  is the sample size, and is not the same as an estimated covariance matrix for variables.
is the sample size, and is not the same as an estimated covariance matrix for variables.
The following statements combine the results for the imputed data sets, and derive both univariate and multivariate inferences about the means. The EDF= option is specified to request that the adjusted degrees of freedom be used in the analysis. For sample means based on 31 observations, the complete-data error degrees of freedom is 30.
proc mianalyze data=outcov edf=30; modeleffects Oxygen RunTime RunPulse; run;
The "Variance Information" and "Parameter Estimates" tables display the same results as in Output 57.1.2 and Output 57.1.3, respectively, in Example 57.1.
With the WCOV, BCOV, and TCOV options, as in the following statements, the procedure displays the between-imputation covariance matrix, within-imputation covariance matrix, and total covariance matrix assuming that the between-imputation covariance matrix is proportional to the within-imputation covariance matrix in Output 57.2.2.
proc mianalyze data=outcov edf=30 wcov bcov tcov mult; modeleffects Oxygen RunTime RunPulse; run;
| Within-Imputation Covariance Matrix | |||
|---|---|---|---|
| Oxygen | RunTime | RunPulse | |
| Oxygen | 0.930852655 | -0.226506411 | -0.461022083 |
| RunTime | -0.226506411 | 0.073141598 | 0.080316017 |
| RunPulse | -0.461022083 | 0.080316017 | 3.114441784 |
| Between-Imputation Covariance Matrix | |||
|---|---|---|---|
| Oxygen | RunTime | RunPulse | |
| Oxygen | 0.0414778123 | 0.0099248946 | 0.0183701754 |
| RunTime | 0.0099248946 | 0.0029478891 | 0.0091684769 |
| RunPulse | 0.0183701754 | 0.0091684769 | 0.1910855259 |
| Total Covariance Matrix | |||
|---|---|---|---|
| Oxygen | RunTime | RunPulse | |
| Oxygen | 1.202882661 | -0.292700068 | -0.595750001 |
| RunTime | -0.292700068 | 0.094516313 | 0.103787365 |
| RunPulse | -0.595750001 | 0.103787365 | 4.024598310 |
With the MULT option, the procedure assumes that the between-imputation covariance matrix is proportional to the within-imputation covariance matrix and displays a multivariate inference for all the parameters taken jointly.
| Multivariate Inference Assuming Proportionality of Between/Within Covariance Matrices |
||||
|---|---|---|---|---|
| Avg Relative Increase in Variance |
Num DF | Den DF | F for H0: Parameter=Theta0 |
Pr > F |
| 0.292237 | 3 | 122.68 | 12519.7 | <.0001 |
The "Multivariate Inference" table in Output 57.2.3 shows a significant 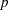 -value for the null hypothesis that the population means are all equal to zero.
-value for the null hypothesis that the population means are all equal to zero.