The GLMSELECT Procedure
-
Overview
- Getting Started
-
Syntax
-
Details
Model-Selection Methods Model Selection Issues Criteria Used in Model Selection Methods CLASS Variable Parameterization and the SPLIT Option Macro Variables Containing Selected Models Using the STORE Statement Building the SSCP Matrix Model Averaging Using Validation and Test Data Cross Validation Displayed Output ODS Table Names ODS Graphics
-
Examples
- References
Least Angle Regression (LAR)
Least angle regression was introduced by Efron et al. (2004). Not only does this algorithm provide a selection method in its own right, but with one additional modification it can be used to efficiently produce LASSO solutions. Just like the forward selection method, the LAR algorithm produces a sequence of regression models where one parameter is added at each step, terminating at the full least squares solution when all parameters have entered the model.
The algorithm starts by centering the covariates and response, and scaling the covariates so that they all have the same corrected sum of squares. Initially all coefficients are zero, as is the predicted response. The predictor that is most correlated with the current residual is determined and a step is taken in the direction of this predictor. The length of this step determines the coefficient of this predictor and is chosen so that some other predictor and the current predicted response have the same correlation with the current residual. At this point, the predicted response moves in the direction that is equiangular between these two predictors. Moving in this direction ensures that these two predictors continue to have a common correlation with the current residual. The predicted response moves in this direction until a third predictor has the same correlation with the current residual as the two predictors already in the model. A new direction is determined that is equiangular between these three predictors and the predicted response moves in this direction until a fourth predictor joins the set having the same correlation with the current residual. This process continues until all predictors are in the model.
As with other selection methods, the issue of when to stop the selection process is crucial. You can specify a criterion to use to choose among the models at each step with the CHOOSE= option. You can also specify a stopping criterion with the STOP= option. See the section Criteria Used in Model Selection Methods for details and Table 44.7 for the formulas for evaluating these criteria. These formulas use the approximation that at step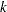 
of the LAR algorithm, the model has 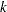degrees of freedom. See Efron et al. (2004) for a detailed discussion of this so-called simple approximation.
A modification of LAR selection suggested in Efron et al. (2004) uses the LAR algorithm to select the set of covariates in the model at any step, but uses ordinary least squares regression with just these covariates to obtain the regression coefficients. You can request this hybrid method by specifying the LSCOEFFS suboption of SELECTION=LAR.