The CATMOD Procedure
-
Overview

-
Getting Started

-
Syntax

-
Details
 Missing Values Input Data Sets Ordering of Populations and Responses Specification of Effects Output Data Sets Logistic Analysis Log-Linear Model Analysis Repeated Measures Analysis Generation of the Design Matrix Cautions Computational Method Computational Formulas Memory and Time Requirements Displayed Output ODS Table Names
Missing Values Input Data Sets Ordering of Populations and Responses Specification of Effects Output Data Sets Logistic Analysis Log-Linear Model Analysis Repeated Measures Analysis Generation of the Design Matrix Cautions Computational Method Computational Formulas Memory and Time Requirements Displayed Output ODS Table Names -
Examples
 Linear Response Function, r=2 Responses Mean Score Response Function, r=3 Responses Logistic Regression, Standard Response Function Log-Linear Model, Three Dependent Variables Log-Linear Model, Structural and Sampling Zeros Repeated Measures, 2 Response Levels, 3 Populations Repeated Measures, 4 Response Levels, 1 Population Repeated Measures, Logistic Analysis of Growth Curve Repeated Measures, Two Repeated Measurement Factors Direct Input of Response Functions and Covariance Matrix Predicted Probabilities
Linear Response Function, r=2 Responses Mean Score Response Function, r=3 Responses Logistic Regression, Standard Response Function Log-Linear Model, Three Dependent Variables Log-Linear Model, Structural and Sampling Zeros Repeated Measures, 2 Response Levels, 3 Populations Repeated Measures, 4 Response Levels, 1 Population Repeated Measures, Logistic Analysis of Growth Curve Repeated Measures, Two Repeated Measurement Factors Direct Input of Response Functions and Covariance Matrix Predicted Probabilities - References
Example 29.11 Predicted Probabilities
Suppose you have collected marketing research data to examine the relationship between a prospect’s likelihood of buying your product and the person’s education and income. Specifically, the variables are as follows:
Variable |
Levels |
Interpretation |
|---|---|---|
Education |
high, low |
Prospect’s education level |
Income |
high, low |
Prospect’s income level |
Purchase |
yes, no |
Did prospect purchase product? |
The following statements first create a data set, loan, that contains the marketing research data. Then the CATMOD procedure fits a model, obtains the parameter estimates, and obtains the predicted probabilities of interest. These statements produce Output 29.11.1 and Output 29.11.2.
data loan; input Education $ Income $ Purchase $ wt; datalines; high high yes 54 high high no 23 high low yes 41 high low no 12 low high yes 35 low high no 42 low low yes 19 low low no 8 ;
ods output PredictedValues=Predicted (keep=Education Income PredFunction); proc catmod data=loan order=data; weight wt; response marginals; model Purchase=Education Income / pred design; run;
proc sort data=Predicted; by descending PredFunction; run; proc print data=Predicted; run;
Notice that the preceding statements use the Output Delivery System (ODS) to output the parameter estimates instead of the OUT= option, though either can be used.
| Complex Sample Survey Analysis |
| Data Summary | |||
|---|---|---|---|
| Response | Purchase | Response Levels | 2 |
| Weight Variable | wt | Populations | 4 |
| Data Set | LOAN | Total Frequency | 234 |
| Frequency Missing | 0 | Observations | 8 |
| Population Profiles | |||
|---|---|---|---|
| Sample | Education | Income | Sample Size |
| 1 | high | high | 77 |
| 2 | high | low | 53 |
| 3 | low | high | 77 |
| 4 | low | low | 27 |
| Response Profiles | |
|---|---|
| Response | Purchase |
| 1 | yes |
| 2 | no |
| Response Functions and Design Matrix | ||||
|---|---|---|---|---|
| Sample | Response Function |
Design Matrix | ||
| 1 | 2 | 3 | ||
| 1 | 0.70130 | 1 | 1 | 1 |
| 2 | 0.77358 | 1 | 1 | -1 |
| 3 | 0.45455 | 1 | -1 | 1 |
| 4 | 0.70370 | 1 | -1 | -1 |
| Analysis of Variance | |||
|---|---|---|---|
| Source | DF | Chi-Square | Pr > ChiSq |
| Intercept | 1 | 418.36 | <.0001 |
| Education | 1 | 8.85 | 0.0029 |
| Income | 1 | 4.70 | 0.0302 |
| Residual | 1 | 1.84 | 0.1745 |
| Analysis of Weighted Least Squares Estimates | |||||
|---|---|---|---|---|---|
| Parameter | Estimate | Standard Error |
Chi- Square |
Pr > ChiSq | |
| Intercept | 0.6481 | 0.0317 | 418.36 | <.0001 | |
| Education | high | 0.0924 | 0.0311 | 8.85 | 0.0029 |
| Income | high | -0.0675 | 0.0312 | 4.70 | 0.0302 |
| Predicted Values for Response Functions | |||||||
|---|---|---|---|---|---|---|---|
| Education | Income | Function Number |
Observed | Predicted | Residual | ||
| Function | Standard Error |
Function | Standard Error |
||||
| high | high | 1 | 0.701299 | 0.052158 | 0.67294 | 0.047794 | 0.028359 |
| high | low | 1 | 0.773585 | 0.057487 | 0.808034 | 0.051586 | -0.03445 |
| low | high | 1 | 0.454545 | 0.056744 | 0.48811 | 0.051077 | -0.03356 |
| low | low | 1 | 0.703704 | 0.087877 | 0.623204 | 0.064867 | 0.080499 |
| Complex Sample Survey Analysis |
| Obs | Education | Income | PredFunction |
|---|---|---|---|
| 1 | high | low | 0.808034 |
| 2 | high | high | 0.67294 |
| 3 | low | low | 0.623204 |
| 4 | low | high | 0.48811 |
You can use the predicted values (values of PredFunction in Output 29.11.2) as scores representing the likelihood that a randomly chosen subject from one of these populations will purchase the product. Notice that the "Response Profiles" table in Output 29.11.1 shows you that the first sorted level of Purchase is 'yes', indicating that the predicted probabilities are for Pr(Purchase='yes'). For example, someone with high education and low income has an estimated probability of purchase of 0.808. Like any response function estimate given by PROC CATMOD, this estimate can be obtained by cross-multiplying the row from the design matrix corresponding to the sample (sample number 2 in this case) with the vector of parameter estimates: 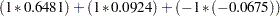 .
.
This ranking of scores can help in decision making (for example, with respect to allocation of advertising dollars, choice of advertising media, choice of print media, and so on).