The CANDISC Procedure
| Displayed Output |
The displayed output from PROC CANDISC includes the class level information table. For each level of the classification variable, the following information is provided: the output data set variable name, frequency sum, weight sum, and the proportion of the total sample.
The optional output from PROC CANDISC includes the following:
Within-class SSCP matrices for each group
Pooled within-class SSCP matrix
Between-class SSCP matrix
Total-sample SSCP matrix
Within-class covariance matrices for each group
Pooled within-class covariance matrix
Between-class covariance matrix, equal to the between-class SSCP matrix divided by
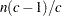 , where n is the number of observations and c is the number of classes
, where n is the number of observations and c is the number of classes Total-sample covariance matrix
Within-class correlation coefficients and
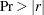 to test the hypothesis that the within-class population correlation coefficients are zero
to test the hypothesis that the within-class population correlation coefficients are zero Pooled within-class correlation coefficients and
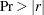 to test the hypothesis that the partial population correlation coefficients are zero
to test the hypothesis that the partial population correlation coefficients are zero Between-class correlation coefficients and
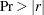 to test the hypothesis that the between-class population correlation coefficients are zero
to test the hypothesis that the between-class population correlation coefficients are zero Total-sample correlation coefficients and
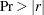 to test the hypothesis that the total population correlation coefficients are zero
to test the hypothesis that the total population correlation coefficients are zero Simple statistics, including N (the number of observations), sum, mean, variance, and standard deviation both for the total sample and within each class
Total-sample standardized class means, obtained by subtracting the grand mean from each class mean and dividing by the total sample standard deviation
Pooled within-class standardized class means, obtained by subtracting the grand mean from each class mean and dividing by the pooled within-class standard deviation
Pairwise squared distances between groups
Univariate test statistics, including total-sample standard deviations, pooled within-class standard deviations, between-class standard deviations, R square,
 , F, and
, F, and 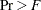 (univariate F values and probability levels for one-way analyses of variance)
(univariate F values and probability levels for one-way analyses of variance)
By default, PROC CANDISC displays these statistics:
Multivariate statistics and F approximations including Wilks’ lambda, Pillai’s trace, Hotelling-Lawley trace, and Roy’s greatest root with F approximations, numerator and denominator degrees of freedom (Num DF and Den DF), and probability values
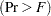 . Each of these four multivariate statistics tests the hypothesis that the class means are equal in the population. See the section Multivariate Tests in
Chapter 4,
Introduction to Regression Procedures,
for more information.
. Each of these four multivariate statistics tests the hypothesis that the class means are equal in the population. See the section Multivariate Tests in
Chapter 4,
Introduction to Regression Procedures,
for more information. Canonical correlations
Adjusted canonical correlations (Lawley; 1959). These are asymptotically less biased than the raw correlations and can be negative. The adjusted canonical correlations might not be computable and are displayed as missing values if two canonical correlations are nearly equal or if some are close to zero. A missing value is also displayed if an adjusted canonical correlation is larger than a previous adjusted canonical correlation.
Approximate standard error of the canonical correlations
Squared canonical correlations
Eigenvalues of
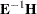 . Each eigenvalue is equal to
. Each eigenvalue is equal to 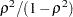 , where
, where 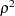 is the corresponding squared canonical correlation and can be interpreted as the ratio of between-class variation to pooled within-class variation for the corresponding canonical variable. The table includes Eigenvalues, Differences between successive eigenvalues, the Proportion of the sum of the eigenvalues, and the Cumulative proportion.
is the corresponding squared canonical correlation and can be interpreted as the ratio of between-class variation to pooled within-class variation for the corresponding canonical variable. The table includes Eigenvalues, Differences between successive eigenvalues, the Proportion of the sum of the eigenvalues, and the Cumulative proportion. Likelihood ratio for the hypothesis that the current canonical correlation and all smaller ones are zero in the population. The likelihood ratio for the hypothesis that all canonical correlations equal zero is Wilks’ lambda.
Approx F statistic based on Rao’s approximation to the distribution of the likelihood ratio (Rao; 1973, p. 556; Kshirsagar; 1972, p. 326)
Numerator degrees of freedom (Num DF), denominator degrees of freedom (Den DF), and
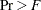 , the probability level associated with the F statistic
, the probability level associated with the F statistic
The following statistics can be suppressed with the SHORT option:
Total canonical structure, giving total-sample correlations between the canonical variables and the original variables
Between canonical structure, giving between-class correlations between the canonical variables and the original variables
Pooled within canonical structure, giving pooled within-class correlations between the canonical variables and the original variables
Total-sample standardized canonical coefficients, standardized to give canonical variables with zero mean and unit pooled within-class variance when applied to the total-sample standardized variables
Pooled within-class standardized canonical coefficients, standardized to give canonical variables with zero mean and unit pooled within-class variance when applied to the pooled within-class standardized variables
Raw canonical coefficients, standardized to give canonical variables with zero mean and unit pooled within-class variance when applied to the centered variables
Class means on the canonical variables
