| Multivariate Tests |
Multivariate hypotheses involve several dependent variables in the form
 |
where  is a linear function on the regressor side,
is a linear function on the regressor side,  is a matrix of parameters,
is a matrix of parameters,  is a linear function on the dependent side, and
is a linear function on the dependent side, and 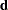 is a matrix of constants. The special case (handled by PROC REG) in which the constants are the same for each dependent variable is expressed as
is a matrix of constants. The special case (handled by PROC REG) in which the constants are the same for each dependent variable is expressed as
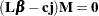 |
where  is a column vector of constants and
is a column vector of constants and  is a row vector of 1s. The special case in which the constants are 0 is then
is a row vector of 1s. The special case in which the constants are 0 is then
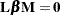 |
These multivariate tests are covered in detail in Morrison (1976), Timm (1975), Mardia, Kent, and Bibby (1979), Bock (1975), and other works cited in Chapter 9, Introduction to Multivariate Procedures.
Notice that in contrast to the tests discussed in the preceding section,  here is a matrix of parameter estimates. Suppose that the matrix of estimates is denoted as
here is a matrix of parameter estimates. Suppose that the matrix of estimates is denoted as 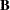 . To test the multivariate hypothesis, construct two matrices,
. To test the multivariate hypothesis, construct two matrices,  and
and 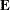 , that correspond to the numerator and denominator of a univariate
, that correspond to the numerator and denominator of a univariate  test:
test:
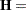 |
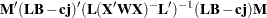 |
|||
 |
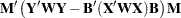 |
Four test statistics, based on the eigenvalues of 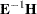 or
or 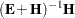 , are formed. Let
, are formed. Let 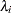 be the ordered eigenvalues of
be the ordered eigenvalues of  (if the inverse exists), and let
(if the inverse exists), and let  be the ordered eigenvalues of
be the ordered eigenvalues of  . It happens that
. It happens that  and
and 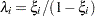 , and it turns out that
, and it turns out that 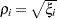 is the
is the  th canonical correlation.
th canonical correlation.
Let 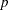 be the rank of
be the rank of  , which is less than or equal to the number of columns of
, which is less than or equal to the number of columns of  . Let
. Let 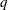 be the rank of
be the rank of 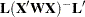 . Let
. Let  be the error degrees of freedom and
be the error degrees of freedom and  . Let
. Let 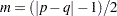 , and let
, and let 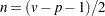 . Then the following statistics test the multivariate hypothesis in various ways, and their p-values can be approximated by
. Then the following statistics test the multivariate hypothesis in various ways, and their p-values can be approximated by  distributions. Note that in the special case that the rank of
distributions. Note that in the special case that the rank of  is 1, all of these
is 1, all of these  statistics will be the same and the corresponding p-values will in fact be exact, since in this case the hypothesis is really univariate.
statistics will be the same and the corresponding p-values will in fact be exact, since in this case the hypothesis is really univariate.
Wilks’ Lambda
 |
then
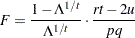 |
is approximately  distributed, where
distributed, where
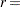 |
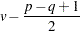 |
|||
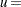 |
 |
|||
 |
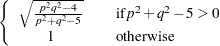 |
The degrees of freedom are 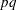 and
and 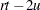 . The distribution is exact if
. The distribution is exact if  . (See Rao 1973, p. 556.)
. (See Rao 1973, p. 556.)
Hotelling-Lawley Trace
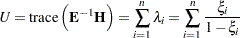 |
then for 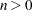
 |
is approximately  distributed with
distributed with 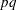 and
and 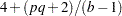 degrees of freedom, where
degrees of freedom, where 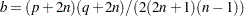 and
and 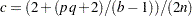 ; while for
; while for 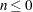
 |
is approximately  with
with  and
and  degrees of freedom.
degrees of freedom.
Roy’s Maximum Root
 |
where 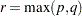 is an upper bound on
is an upper bound on  that yields a lower bound on the significance level. Degrees of freedom are
that yields a lower bound on the significance level. Degrees of freedom are  for the numerator and
for the numerator and 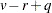 for the denominator.
for the denominator.
Tables of critical values for these statistics are found in Pillai (1960).
Exact Multivariate Tests
Beginning with SAS 9, if you specify the MSTAT=EXACT option in the appropriate statement, p-values for three of the four tests are computed exactly (Wilks’ lambda, the Hotelling-Lawley trace, and Roy’s greatest root), and the p-values for the fourth (Pillai’s trace) are based on an  approximation that is more accurate (but occasionally slightly more liberal) than the default. The exact p-values for Roy’s greatest root benefit the most, since in this case the
approximation that is more accurate (but occasionally slightly more liberal) than the default. The exact p-values for Roy’s greatest root benefit the most, since in this case the  approximation provides only a lower bound for the
approximation provides only a lower bound for the 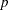 -value. If you use the
-value. If you use the  -based
-based 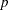 -value for this test in the usual way, declaring a test significant if
-value for this test in the usual way, declaring a test significant if 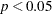 , then your decisions might be very liberal. For example, instead of the nominal 5% Type I error rate, such a procedure can easily have an actual Type I error rate in excess of 30%. By contrast, basing such a procedure on the exact p-values will result in the appropriate 5% Type I error rate, under the usual regression assumptions.
, then your decisions might be very liberal. For example, instead of the nominal 5% Type I error rate, such a procedure can easily have an actual Type I error rate in excess of 30%. By contrast, basing such a procedure on the exact p-values will result in the appropriate 5% Type I error rate, under the usual regression assumptions.
The MSTAT=EXACT option is supported in the ANOVA, CANCORR, CANDISC, GLM, and REG procedures.
The exact 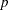 -values are based on the following sources:
-values are based on the following sources:
Wilks’ lambda: Lee (1972), Davis (1979)
Pillai’s trace: Muller (1998)
Hotelling-Lawley trace: Davis (1970), Davis (1980)
Roy’s greatest root: Davis (1972), Pillai and Flury (1984)
Note that, although the MSTAT=EXACT 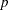 -value for Pillai’s trace is still approximate, it has "substantially greater accuracy" than the default approximation (Muller 1998).
-value for Pillai’s trace is still approximate, it has "substantially greater accuracy" than the default approximation (Muller 1998).
Since most of the MSTAT=EXACT 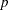 -values are not based on the
-values are not based on the  distribution, the columns in the multivariate tests table corresponding to this approximation—in particular, the
distribution, the columns in the multivariate tests table corresponding to this approximation—in particular, the  value and the numerator and denominator degrees of freedom—are no longer displayed, and the column containing the
value and the numerator and denominator degrees of freedom—are no longer displayed, and the column containing the 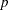 -values is labeled “P Value” instead of "Pr > F." Suppose, for example, you use the following PROC ANOVA statements to perform a multivariate analysis of an archaeological data set:
-values is labeled “P Value” instead of "Pr > F." Suppose, for example, you use the following PROC ANOVA statements to perform a multivariate analysis of an archaeological data set:
data Skulls; input Loc $20. Basal Occ Max; datalines; Minas Graes, Brazil 2.068 2.070 1.580 Minas Graes, Brazil 2.068 2.074 1.602 Minas Graes, Brazil 2.090 2.090 1.613 Minas Graes, Brazil 2.097 2.093 1.613 Minas Graes, Brazil 2.117 2.125 1.663 Minas Graes, Brazil 2.140 2.146 1.681 Matto Grosso, Brazil 2.045 2.054 1.580 Matto Grosso, Brazil 2.076 2.088 1.602 Matto Grosso, Brazil 2.090 2.093 1.643 Matto Grosso, Brazil 2.111 2.114 1.643 Santa Cruz, Bolivia 2.093 2.098 1.653 Santa Cruz, Bolivia 2.100 2.106 1.623 Santa Cruz, Bolivia 2.104 2.101 1.653 ;
proc anova data=Skulls; class Loc; model Basal Occ Max = Loc / nouni; manova h=Loc; ods select MultStat; run;
The default multivariate tests, based on the  approximations, are shown in Figure 4.5.
approximations, are shown in Figure 4.5.
| MANOVA Test Criteria and F Approximations for the Hypothesis of No Overall Loc Effect H = Anova SSCP Matrix for Loc E = Error SSCP Matrix S=2 M=0 N=3 |
|||||
|---|---|---|---|---|---|
| Statistic | Value | F Value | Num DF | Den DF | Pr > F |
| Wilks' Lambda | 0.60143661 | 0.77 | 6 | 16 | 0.6032 |
| Pillai's Trace | 0.44702843 | 0.86 | 6 | 18 | 0.5397 |
| Hotelling-Lawley Trace | 0.58210348 | 0.75 | 6 | 9.0909 | 0.6272 |
| Roy's Greatest Root | 0.35530890 | 1.07 | 3 | 9 | 0.4109 |
| NOTE: F Statistic for Roy's Greatest Root is an upper bound. | |||||
| NOTE: F Statistic for Wilks' Lambda is exact. | |||||
If you specify MSTAT=EXACT in the MANOVA statement, as in the following statements, then the displayed output is the much simpler table shown in Figure 4.6.
proc anova data=Skulls; class Loc; model Basal Occ Max = Loc / nouni; manova h=Loc / mstat=exact; ods select MultStat; run;
| MANOVA Tests for the Hypothesis of No Overall Loc Effect H = Anova SSCP Matrix for Loc E = Error SSCP Matrix S=2 M=0 N=3 |
||
|---|---|---|
| Statistic | Value | P-Value |
| Wilks' Lambda | 0.60143661 | 0.6032 |
| Pillai's Trace | 0.44702843 | 0.5521 |
| Hotelling-Lawley Trace | 0.58210348 | 0.6337 |
| Roy's Greatest Root | 0.35530890 | 0.7641 |
Notice that the 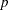 -value for Roy’s greatest root is substantially larger in the new table, and correspondingly more in line with the
-value for Roy’s greatest root is substantially larger in the new table, and correspondingly more in line with the 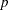 -values for the other tests.
-values for the other tests.
If you reference the underlying ODS output object for the table of multivariate statistics, it is important to note that its structure does not depend on the value of the MSTAT= specification. In particular, it always contains columns corresponding to both the default MSTAT=FAPPROX and the MSTAT=EXACT tests. Moreover, since the MSTAT=FAPPROX tests are relatively cheap to compute, the columns corresponding to them are always filled in, even though they are not displayed when you specify MSTAT=EXACT. On the other hand, for MSTAT=FAPPROX (which is the default), the column of exact 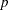 -values contains missing values, and is not displayed.
-values contains missing values, and is not displayed.
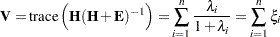
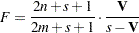
 degrees of freedom.
degrees of freedom. 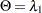 , then
, then