| The SEQDESIGN Procedure |
| DESIGN Statement |
The DESIGN statement requests a new group sequential design. You can use multiple DESIGN statements, and each DESIGN statement corresponds to a separate group sequential design.
Table 78.2 lists the options available in the DESIGN statement.
Option |
Description |
|---|---|
Design Parameters |
|
ALPHA= |
Specifies the Type I error probability level |
ALT= |
Specifies the type of alternative hypothesis |
BETA= |
Specifies the Type II error probability level |
BETAOVERLAP= |
Checks for overlapping of the lower and upper |
in a two-sided design with error spending methods |
|
BOUNDARYKEY= |
Specifies the type of error probability to maintain |
INFO= |
Specifies the information levels |
NSTAGES= |
Specifies the number of stages |
STOP= |
Specifies the condition for early stopping |
Boundary Methods |
|
METHOD= |
Specifies methods for boundary values |
The required NSTAGES= option specifies the number of stages. The METHOD= option is required if the number of stages specified in the NSTAGES= option is greater than one. The following options can be used in the DESIGN statement. They are listed in alphabetical order.
-
ALPHA=
 <( <LOWER=
<( <LOWER=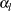 > <UPPER=
> <UPPER=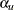 > )>
> )>
specifies the Type I error probability
 . The default is
. The default is 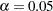 . The LOWER= and UPPER= options are applicable only for the two-sided design. The LOWER= option specifies the lower Type I error probability
. The LOWER= and UPPER= options are applicable only for the two-sided design. The LOWER= option specifies the lower Type I error probability 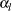 , and the upper Type I error probability is computed as
, and the upper Type I error probability is computed as 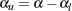 . The UPPER= option specifies the upper Type I error probability
. The UPPER= option specifies the upper Type I error probability 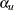 , and the lower Type I error probability is computed as
, and the lower Type I error probability is computed as 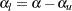 . If both LOWER= and UPPER= options are not specified,
. If both LOWER= and UPPER= options are not specified, 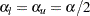 .
. If both the MAXINFO= and ALTREF= options are specified, then the Type I and Type II error probability levels cannot be met simultaneously. In this case, the ALPHA= option is applicable only with the BOUNDARYKEY=ALPHA option (which is the default), and the Type II error probability
 is derived.
is derived. - ALT=LOWER | UPPER | TWOSIDED
specifies the type of alternative hypothesis in the design. For a test of
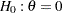 , the keywords LOWER, UPPER, and TWOSIDED correspond to the alternatives of
, the keywords LOWER, UPPER, and TWOSIDED correspond to the alternatives of 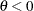 ,
, 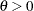 , and
, and 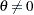 , respectively. The default is ALT=TWOSIDED.
, respectively. The default is ALT=TWOSIDED. -
BETA=
 <( <LOWER=
<( <LOWER=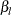 > <UPPER=
> <UPPER=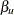 > )>
> )>
specifies the Type II error probability level
 . The default is
. The default is 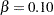 . The LOWER= and UPPER= options are applicable only for the two-sided design. The LOWER= option specifies the lower Type II error probability level
. The LOWER= and UPPER= options are applicable only for the two-sided design. The LOWER= option specifies the lower Type II error probability level 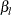 , and the UPPER= option specifies the upper Type II error probability level
, and the UPPER= option specifies the upper Type II error probability level 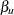 . If the LOWER= or UPPER= option is not specified,
. If the LOWER= or UPPER= option is not specified,  is used.
is used. If both the MAXINFO= and ALTREF= options are specified, then the Type I and Type II error probability levels cannot be met simultaneously. In this case, the BETA= option is applicable only with the BOUNDARYKEY=BETA option, and the Type I error probability
 is derived.
is derived. - BETAOVERLAP=ADJUST | NOADJUST
- OVERLAP=ADJUST | NOADJUST
specifies whether to check for overlapping of the lower and upper
 boundaries for the two corresponding one-sided tests. This option applies to two-sided designs with STOP=ACCEPT or STOP=BOTH that are constructed with error spending methods, and this type of overlapping might result from a small
boundaries for the two corresponding one-sided tests. This option applies to two-sided designs with STOP=ACCEPT or STOP=BOTH that are constructed with error spending methods, and this type of overlapping might result from a small  spending at an interim stage. When you specify BETAOVERLAP=ADJUST, the procedure checks for this type of overlapping. If such overlapping is found, the
spending at an interim stage. When you specify BETAOVERLAP=ADJUST, the procedure checks for this type of overlapping. If such overlapping is found, the  boundaries for the two-sided design at that stage are set to missing, and the
boundaries for the two-sided design at that stage are set to missing, and the  spending values at subsequent stages are adjusted, as described in the section Boundary Adjustments for Overlapping Lower and Upper
spending values at subsequent stages are adjusted, as described in the section Boundary Adjustments for Overlapping Lower and Upper 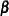 Boundaries".
Boundaries". You can specify BETAOVERLAP=NOADJUST to request that no adjustment be made. The default is BETAOVERLAP=ADJUST.
- BOUNDARYKEY=ALPHA | BETA | BOTH | NONE
specifies types of errors to be maintained in the resulting boundary. The default is BOUNDARYKEY=ALPHA if both ALTREF= and MAXINFO= options are specified. Otherwise, the default is BOUNDARYKEY=NONE for Whitehead methods with the STOP=BOTH option, and it is BOUNDARYKEY=BOTH for others.
See the section Applicable Boundary Keys for a detailed description of applicable boundary keys.
- INFO=EQUAL
- INFO=CUM( numbers )
specifies relative information levels for all stages in the design. The INFO=EQUAL option specifies equally spaced information levels, and the INFO=CUM option specifies cumulative relative information levels. The default is INFO=EQUAL.
If the number of information levels specified in the INFO=CUM option is less than the number of stages specified in the NSTAGES= option, the last available information increment is used as the information increment for each subsequent stage.
-
METHOD=WHITEHEAD < ( TAU=
 < ( <LOWER=
< ( <LOWER=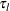 > <UPPER=
> <UPPER=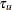 > ) > ) >
> ) > ) >
- METHOD=method
- METHOD(boundary) = method
specifies the methods for the boundaries in the design, where
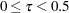 .
. For a one-sided design, an
 boundary is created with the STOP=REJECT or STOP=BOTH option, and a
boundary is created with the STOP=REJECT or STOP=BOTH option, and a  boundary is created with the STOP=ACCEPT or STOP=BOTH option. For a two-sided design, lower and upper
boundary is created with the STOP=ACCEPT or STOP=BOTH option. For a two-sided design, lower and upper  boundaries are created with the STOP=REJECT or STOP=BOTH option, and lower and upper
boundaries are created with the STOP=REJECT or STOP=BOTH option, and lower and upper  boundaries are created with the STOP=ACCEPT or STOP=BOTH option.
boundaries are created with the STOP=ACCEPT or STOP=BOTH option. There are three types of methods available in the SEQDESIGN procedure. The unified family methods and Haybittle-Peto methods derive boundary values with fixed boundary shape; the Whitehead methods derive boundary values by adjusting the boundary values generated from continuous monitoring; and the error spending methods derive the boundary values from the specified errors used at each stage. You can specify different methods for the same design, but all methods must be from the same group.
For a design with early stopping to reject or accept the null hypothesis, the METHOD=WHITEHEAD option uses Whitehead’s triangular design and double-triangular design for a one-sided design and two-sided design, respectively (Whitehead and Stratton 1983; Whitehead 1997, 2001). For a design with early stopping only to reject the null hypothesis or only to accept the null hypothesis, you can specify the slope of the boundary line in the score statistic scale with the TAU= option. The default is TAU=
option. The default is TAU= . See the section Whitehead Methods for a detailed description of the Whitehead methods.
. See the section Whitehead Methods for a detailed description of the Whitehead methods. The following options specify available error spending methods for the boundary. Each of these methods can be specified with the METHOD= option for all boundaries, or with the METHOD(boundary) = option for an individual boundary. See the section Error Spending Methods for a detailed description of these error spending methods.
-
ERRFUNCGAMMA < ( GAMMA=
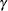 ) >
) >
specifies a gamma cumulative error spending function for the boundary (Hwang, Shih, and DeCani 1990). The GAMMA= option specifies the gamma parameter
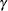 in the function, where
in the function, where 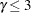 . The boundaries created with
. The boundaries created with 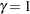 are similar to the boundaries from the Pocock method, and the boundaries created with
are similar to the boundaries from the Pocock method, and the boundaries created with 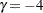 or
or 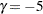 are similar to the boundaries from the O’Brien-Fleming method. The default is GAMMA=
are similar to the boundaries from the O’Brien-Fleming method. The default is GAMMA=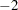 , which is the average of
, which is the average of 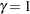 and
and 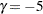 .
. - ERRFUNCOBF
specifies the O’Brien-Fleming-type cumulative error spending function for the boundary (Lan and DeMets 1983).
- ERRFUNCPOC
specifies the Pocock-type cumulative error spending function for the boundary (Lan and DeMets 1983).
-
ERRFUNCPOW < ( RHO=
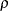 ) >
) >
specifies a power cumulative error spending function for the boundary (Jennison and Turnbull 2000, p. 148). The RHO= option specifies the power parameter
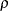 in the function, where
in the function, where 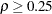 . The boundaries created with
. The boundaries created with 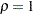 are similar to the boundaries from the Pocock method, and the boundaries created with
are similar to the boundaries from the Pocock method, and the boundaries created with 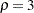 are similar to the boundaries from the O’Brien-Fleming method. The default is RHO=2, which is the average of
are similar to the boundaries from the O’Brien-Fleming method. The default is RHO=2, which is the average of 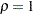 and
and 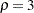 .
. - ERRSPEND ( numbers )
specifies the relative cumulative error spending at each stage.
With a fixed boundary shape, you can use the following available Haybittle-Peto methods and unified family methods to derive the boundary. You can specify each of these methods in the METHOD= option for all boundaries, or in the METHOD(boundary) = option for an individual boundary. See the section Haybittle-Peto Method for a detailed description of the Haybittle-Peto methods, and see the section Unified Family Methods for a detailed description of unified family methods.
- HP | HAYBITTLE | PETO < ( Z= numbers | PVALUE= numbers ) >
specifies the Haybittle-Peto method (Haybittle 1971; Peto et al. 1976). The values specified are used to create the boundary values. The boundary value at the final stage can be derived in the procedure to maintain the Type I and Type II error probability levels. The default is Z=
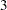 .
. - OBF | OBRIENFLEMING
specifies the O’Brien-Fleming method (O’Brien and Fleming 1979). The O’Brien-Fleming method is equivalent to a power family method with RHO=
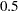 .
. - POC | POCOCK
specifies the Pocock method (Pocock 1977). The Pocock method is equivalent to a power family method with RHO=
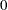 .
. -
POW | POWER < ( RHO=
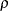 ) >
) >
specifies a power family method (Wang and Tsiatis 1987; Emerson and Fleming 1989; Pampallona and Tsiatis 1994). The RHO= option specifies the power parameter
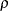 in the power family method, where
in the power family method, where 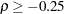 . The power family method with
. The power family method with 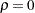 corresponds to the Pocock method, and the power family method with
corresponds to the Pocock method, and the power family method with 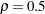 corresponds to the O’Brien-Fleming method. The default is RHO=0.25, a value halfway between the Pocock and O’Brien-Fleming methods. A power family method is equivalent to a unified family method with RHO=
corresponds to the O’Brien-Fleming method. The default is RHO=0.25, a value halfway between the Pocock and O’Brien-Fleming methods. A power family method is equivalent to a unified family method with RHO=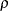 and TAU=
and TAU=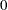 .
. -
TRI | TRIANGULAR < ( TAU=
 ) >
) >
specifies a unified family triangular method (Kittelson and Emerson 1999), where
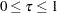 . The default is TAU=1.0. The triangular method is identical to the unified family method with RHO=
. The default is TAU=1.0. The triangular method is identical to the unified family method with RHO=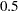 and TAU=
and TAU= . Note that this unified family triangular method is different from Whitehead’s triangular method.
. Note that this unified family triangular method is different from Whitehead’s triangular method. -
UNI | UNIFIED < ( <TAU=
 > <RHO=
> <RHO=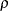 > ) >
> ) >
specifies a unified family method (Kittelson and Emerson 1999). The TAU= and RHO= options specify the
 and
and 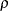 parameters in a unified family method, respectively, where
parameters in a unified family method, respectively, where 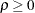 and
and 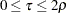 . The defaults are TAU=0 and RHO=0.25. See the section Unified Family Methods for a detailed description of the unified family methods.
. The defaults are TAU=0 and RHO=0.25. See the section Unified Family Methods for a detailed description of the unified family methods.
The O’Brien-Fleming, Pocock, power family, and triangular methods are all special cases of the unified family methods. Table 78.3 summarizes the corresponding parameters in the unified family for these methods.
Table 78.3 Parameters in the Unified Family for Various Methods Method
Option
Unified Family
Rho
Tau
Pocock
POC
0
0
O’Brien-Fleming
OBF
0.5
0
Power family
POW (RHO=
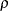 )
) 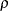
0
Triangular
TRI (TAU=
 )
) 0.5

Note that the power parameter
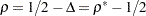 , where
, where 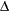 is the power parameter used in Jennison and Turnbull (2000) and Wang and Tsiatis (1987) and
is the power parameter used in Jennison and Turnbull (2000) and Wang and Tsiatis (1987) and 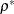 is the power parameter used in Kittelson and Emerson (1999).
is the power parameter used in Kittelson and Emerson (1999). If a method with specified parameters is used for all boundaries in the design, you can use the METHOD= option to specify the method. Otherwise, you can use the following METHOD(boundary)= options to specify different methods from the same group for the boundaries.
-
ERRFUNCGAMMA < ( GAMMA=
- METHOD(ALPHA)=method
- METHOD(REJECT)=method
specifies the method for the
 boundary of a one-sided design or the lower and upper
boundary of a one-sided design or the lower and upper  boundaries for a two-sided design.
boundaries for a two-sided design. - METHOD(LOWERALPHA)=method
- METHOD(LOWERREJECT)=method
specifies the method for the lower
 boundary of a two-sided design.
boundary of a two-sided design. - METHOD(UPPERALPHA)=method
- METHOD(UPPERREJECT)=method
specifies the method for the upper
 boundary of a two-sided design.
boundary of a two-sided design. - METHOD(BETA)=method
- METHOD(ACCEPT)=method
specifies the method for the
 boundary of a one-sided design or the lower and upper
boundary of a one-sided design or the lower and upper  boundaries for a two-sided design.
boundaries for a two-sided design. - METHOD(LOWERBETA)=method
- METHOD(LOWERACCEPT)=method
specifies the method for the lower
 boundary of a two-sided design.
boundary of a two-sided design. - METHOD(UPPERBETA)=method
- METHOD(UPPERACCEPT)=method
specifies the method for the upper
 boundary of a two-sided design.
boundary of a two-sided design. - NSTAGES=number
specifies the number of stages for the design. This option is required in the DESIGN statement, and the maximum allowed number of stages is 25.
- STOP=ACCEPT | REJECT | BOTH
specifies the condition of early stopping for the design. The keywords ACCEPT, REJECT, and BOTH correspond to early stopping only to accept, only to reject, and either to accept or reject the null hypothesis
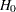 , respectively. The default is STOP=REJECT.
, respectively. The default is STOP=REJECT.
Copyright © SAS Institute, Inc. All Rights Reserved.