| The SEQDESIGN Procedure |
| Error Spending Methods |
For each sequential design, the  and
and  errors spent at each stage can be computed from the boundary values. For example, for a
errors spent at each stage can be computed from the boundary values. For example, for a 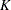 -stage design with an upper alternative hypothesis
-stage design with an upper alternative hypothesis  and early stopping to reject the null hypothesis
and early stopping to reject the null hypothesis  , the boundary values in a standardized
, the boundary values in a standardized 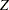 scale are the upper
scale are the upper  critical values
critical values 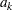 ,
, 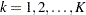 . At each interim stage, the null hypothesis
. At each interim stage, the null hypothesis 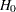 is rejected if the observed standardized
is rejected if the observed standardized 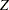 statistic
statistic  . Otherwise, the process continues to the next stage. At the final stage, the hypothesis is rejected if
. Otherwise, the process continues to the next stage. At the final stage, the hypothesis is rejected if 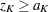 . Otherwise, the null hypothesis is accepted.
. Otherwise, the null hypothesis is accepted.
The boundary values 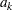 are derived such that the overall Type I error probability
are derived such that the overall Type I error probability
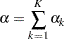 |
where 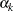 is the
is the  spending at stage
spending at stage 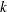 . That is, at stage
. That is, at stage  ,
,
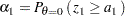 |
At a subsequent stage 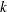 ,
,
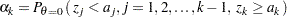 |
Since each design can be uniquely identified by the  and
and  errors spent at each stage, a design can then be derived by specifying the
errors spent at each stage, a design can then be derived by specifying the  and
and  errors to be used at each stage. The error spending method (Lan and DeMets 1983) distributes the error to be used at each stage and then derives the boundary values. Numerous forms of the error spending function are available. Kim and DeMets (1987) examine the functions
errors to be used at each stage. The error spending method (Lan and DeMets 1983) distributes the error to be used at each stage and then derives the boundary values. Numerous forms of the error spending function are available. Kim and DeMets (1987) examine the functions 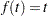 ,
, 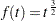 , and
, and 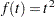 , where
, where  is the information fraction. Jennison and Turnbull (2000, p. 148) generalize these functions to the power functions
is the information fraction. Jennison and Turnbull (2000, p. 148) generalize these functions to the power functions 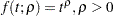 .
.
The ERRFUNCPOC option uses the cumulative error spending function (Lan and DeMets 1983)
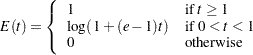 |
With a specified error of  or
or  , the cumulative error spending at stage
, the cumulative error spending at stage  is
is 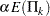 or
or 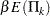 , where
, where 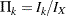 is the information fraction at stage
is the information fraction at stage 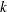 . The method produces boundaries similar to those produced with Pocock’s method.
. The method produces boundaries similar to those produced with Pocock’s method.
The ERRFUNCOBF option uses the cumulative error spending function (Lan and DeMets 1983)
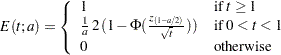 |
where  is either
is either  for the
for the  spending function or
spending function or  for the
for the  spending function. That is, with a specified error of
spending function. That is, with a specified error of  or
or  , the cumulative error spending at stage
, the cumulative error spending at stage 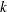 is
is 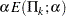 or
or 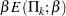 . The method produces boundaries similar to those produced with the O’Brien-Fleming method.
. The method produces boundaries similar to those produced with the O’Brien-Fleming method.
The ERRFUNCGAMMA option uses the gamma cumulative error spending function (Hwang, Shih, and DeCani 1990)
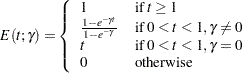 |
where 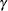 is the parameter
is the parameter 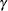 specified in the GAMMA= option. That is, with a specified error of
specified in the GAMMA= option. That is, with a specified error of  or
or  , the cumulative error spending at stage
, the cumulative error spending at stage 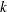 is
is 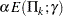 or
or 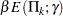 .
.
The ERRFUNCPOW option uses the cumulative error spending function (Jennison and Turnbull 2000, p. 148)
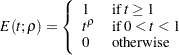 |
where 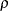 is the power parameter specified in the RHO= option. That is, with a specified error of
is the power parameter specified in the RHO= option. That is, with a specified error of  or
or  , the cumulative error spending at stage
, the cumulative error spending at stage 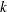 is
is  or
or 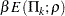 .
.
Error spending methods derive boundary values at each stage sequentially and require much more computation than other types of methods for group sequential trials with a large number of stages, especially for a two-sided asymmetric design with early stopping to accept 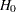 , or to reject or accept
, or to reject or accept 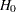 .
.
Note that for a two-sided design with the STOP=BOTH or STOP=ACCEPT option, at each interim stage, the SEQDESIGN procedure first produces the lower and upper  boundary values based on the one-sided
boundary values based on the one-sided  spending. If the lower
spending. If the lower  boundary value is greater than or equal to its corresponding upper
boundary value is greater than or equal to its corresponding upper  boundary value, there is no early stopping to accept the null hypothesis at this stage, and the corresponding
boundary value, there is no early stopping to accept the null hypothesis at this stage, and the corresponding  spending is distributed proportionally to the remaining stages.
spending is distributed proportionally to the remaining stages.
For the error spending functions not available in the SEQDESIGN procedure, you can first compute the corresponding error spending at each stage explicitly, then use the SEQDESIGN procedure with the ERRSPEND= option to specify these errors directly.
For example, if the information levels are equally spaced in a five-stage design, the option ERRFUNCPOW (RHO=2) produces relative cumulative errors of 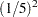 ,
, 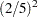 ,
, 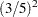 ,
, 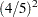 , and 1. This is equivalent to using the option ERRSPEND (1 4 9 16 25).
, and 1. This is equivalent to using the option ERRSPEND (1 4 9 16 25).
A one-sided error spending design is illustrated in Example 78.8 and a two-sided asymmetric error spending design is illustrated in Example 78.11.
Copyright © SAS Institute, Inc. All Rights Reserved.